九年级数学结课质量调查　　　　  学校　　　　 姓名　　　　　 

一，选择题：

每个小题都给出四个选项，其中只有一个选项是正确的，请把正确选项的字母填入表中。填写正确的得3分，不填或多填均得0分。

题号	1	2	3	4	5	6	7	8	9	10
答案

1．已知sin=,且是锐角，则=(　　)

A;75⁰　　　　　　　 B;60⁰　　　　　　　　  C;45⁰　　　　　　　　　 D;30⁰

2.已知关于x的一元二次方程 x²－2x+=0有实根，则实数的取值范围是（　　）

A; ≤1　　　　　 B; <1　　　　　　　  C; ≤－1　　　　　　 D; ≥1

3.用换元法解方程 x²－2x+，若设x²－2x=y，则原方程化为关于y的整式方程是（　　）

A；y²+8y－7=0　　  B；y²－8y－7=0　　　　C；y²+8y+7=0　　　　　 D；y²－8y＋7=0

4.已知一次函数 y=kx－k，若y随x的增大而减小，则该函数的图像经过（　　　）

A;第一，二，三象限，　B; 第一，二，四象限　C; 第二，三，四象限　D; 第一，三，四象限

5．在一次射击练习中，甲，乙两人前5次射击的成绩分别为（单位：环）

甲：10　8  10　10　7

乙：7　10　 9　9　 10

即两人射击成绩的稳定程度是（　　）

A;甲比乙稳定　　　 B;乙比甲稳定　　　　 C;甲，乙的稳定程度相同　D;无法进行比较

6．⊙O₁与⊙O₂的半径分别为2和5，当O₁O₂=2.5时，两圆的位置关系是（　　 ）

A；外切　　　 　　 B；相交　　　　　　 C；内切　　　　　　　  D；内含

7．已知正六边形的外接圆的半径是a，则正六边形的周长是（　　）

A;3a　　　　　　　 B;6a　　　　　　　　 C;2a　　　　　　　　　  D;24a

8.已知：如图⊙O的割线PAB交⊙O于点A,B, PA=7cm, AB=5cm, PO=10cm, 则⊙O的半径是(　　)

A;4cm　　　　　　 B;5cm　　　　　　　  C;6cm　　　　　　　　　 D;7cm

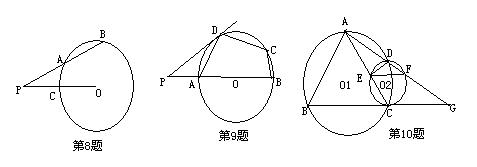
9.已知，如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=130⁰,过D点的切线PD与直线AB交于P点，则∠ADP的度数为(　　)

A;40⁰　　　　　　 B;45⁰　　　　　　  C;50⁰　　　　　　  D;65⁰

10.如图，已知等边三角形△ABC内接于⊙O₁，⊙O₂与BC相切于C，与AC相交于E，与⊙O₁相交于另一点D，直线AD交⊙O₂于另一点F，交BC的延长线于G，点F为AG的中点。对于如下四个结论：①EF∥BC ②BC=FC

③DE·AG=AB·EC ④弧AD=弧DC　其中一定成立的是：（　　）

A;①②④　　　　 B; ②③　　　　　  C; ①③④　　　　  D; ①②③④

二，填空题：每小题3分

11．已知是方程x²+2x－5=0的两个实数根，则的值为　　　　　  。

12.若正比例函数y=kx与y=2x的图像关于x轴对称，则k的值等于　　　　　　 。

13.写出一个图像位于第二，四象限的反比例函数的解析式　　　　　　　  。

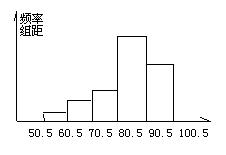
14。为了了解中学生的素质教育情况，某县在全县各中学共抽取了200名九年级学生进行素质教育调查，将所得的数据整理后，划出频率分布直方图（如图），已知图中从左到右前4个小组的频率分别是0.04 ，0.12 ，0.16 ，

0.4 ，则第5小组的频数是　　　　　　　　 。

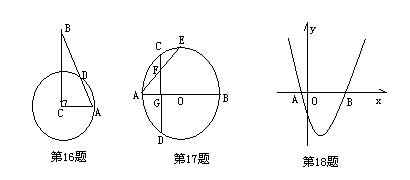
15．圆锥的底面半径为3cm,母线长为5cm,则它的侧面积为　　　　　　  。

16.如图，已知在△ABC中，∠ACB=90⁰,∠B=35⁰,为C圆心，CA为半径的圆交AB于D点,则弧AD为　　　　 .

17.如图，AB是⊙O的直径，弦CD⊥AB，垂足是G，F是CG的中点，延长AF交⊙O于E，CF=2, AF=3, 则EF的长是　　　　 。

18.设函数y=x²－(k+1)x－4(k+5)的图像如图所示，它与x轴交于A,B两点，且线段OA与OB的长的比为1：4，则k=　　　　　　 。

三，解答题：

19．本小题6分

下表是七年级三班30名学生期末考试数学成绩表（已破损）

成绩（分）	50	60	70	80	90	100
人数（人）	2	5	7			3

已知该班学生期末考试数学成绩平均分是76分。（1）求该班80分和90分的人数分别是多少？

（2）设该班30名学生成绩的众数为a,中位数为b, 求a+b的值。

20．本小题8分

如图，抛物线的对称轴是直线x=1 ,它与x轴交于A,B两点,与y轴交于C点,点A,C的坐标分别为（－1，0），（0，）　（1）求此抛物线对应的函数的解析式。　（2）若点P是此抛物线上位于x轴上方的一个动点,求△ABC面积的最大值.

21．本小题8分

如图所示，已知一次函数y=kx+b的图像与x轴y轴分别交于A,B两点，且与反比例函数y=的图像在第一象限交于C点，CD垂直于x轴，垂足为D，若OA=OB=OD=1，

（1）求点A,B,D的坐标。　　 （2）求一次函数与反比例函数的解析式。

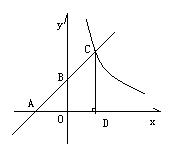
22. 本小题8分

如图所示，四边形ABDE内接⊙O，AE, BD的延长线相交于点C，直径AE为8, OC=12,

（1）求证：　　　　（2）计算CD·CB的值，并指出CB的取值范围。

23. 本小题8分

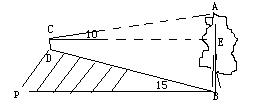
如图，山脚下有一棵树AB,小强从点B沿山坡向上走50米到达点D，用高为1.5米的测角仪CD测得树顶的仰角为10⁰，已知山坡的坡角为15⁰，求树AB的高。

(精确到0.1米，已知sin10⁰=0.17 ,cos10⁰=0.98 ,tan10⁰=0.18 ,sin15⁰=0.26 ,cos15⁰=0.97 ,tan15⁰=0.27)

24. 本小题8分

甲，乙两名工人接受相同数量的生产任务，开始时，乙比甲每天少做4件，乙比甲多用2天时间。这样甲乙两人各剩120件，随后，乙改进了生产技术，而甲每天的工作量不变，结果两人完成全部生产任务所用的时间相同。求：原来甲，乙两人每天各做多少件？

25．本小题10分

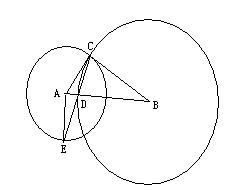
如图，已知⊙A,⊙B都经过点C，BC是⊙A的切线，⊙B交AB于点D，连结CD并延长交⊙A于点E，连结AE

（1）求证：AE⊥AB　　　　　　　  （2）求证：DE·DC=2AD·DB

（3）如果DE·DC=8 ,AE=3，求BC的长。

26. 本小题10分

设抛物线y=ax²+bx+c经过A(－1,2), B(2 ,－1)两点，且与y轴交于点M

（1）　　　 求b和c（用含a的代数式表示）

（2）　　　 求抛物线y=ax²－bx+c－1上横坐标与纵坐标相等的点的坐标

（3）　　　 在第（2）小题所求出的点中，有一个点也在抛物线y=ax²+bx+c上，试判断直线AM和x轴的位置关系，并说明理由。

答案：

一，B,　A,  D,　B,　B,  D,　B,　A,  A,　D

二，(11)0　 (12)－2　(13)答案不唯一　（14）56　(15)15　(16)70⁰　 (17)1　 (18)11

三，(19)8,5人　a+b=160　　 (20)y=－,　4　　　(21)y=x+1, y= ,　  (22)证明略，OC=12

(23)树高约为23.2米。　　　 （24）甲10件，乙6件。　　 （25）证明略， BC=BD=4

(26)b=－a－1,c=1－2a　;P₁(1,1),P₂(－2,－2),  当P₁(1,1)在抛物线上时，直线AM平行于x轴，当P₂(－2,－2)在抛物线上时，直线与相交x轴，