初中毕业生学业考试数学模拟试卷(1)

一、选择题、（本题有10小题，每小题4分，共40分）

1、4的平方根是（　　）

A、2　　　B、±2　　  C 、4　　　D、±4　

2．下列选项中，正确的是（　　 ）

　　A．方程=0的解是x=－1　　　　　B.当x≠1时，公式有意义

　　B.方程=0的解是x=1　　　　　　 D. 当x≠±1时，公式有意义

3、如图Rt△ABC∽Rt△DEF，∠C=∠F=90°，点A与点D为对应点，∠B=60°，则∠E的度数（　　）　　　　　　　　　 

A、30°　　B、45°　　C、60°　　D、90°

4、下面各图是最左边这个几何体的俯视图，其中正确的是(　　 )

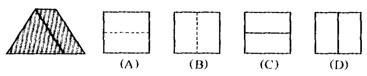
5、二次函数y=2（x–1）²-1的顶点坐标是（　　　）

A （-1，-1）　 B （1，-1）　 C （-1，1）　 D （1，1）

6、已知如图Rt△ABC中，∠C=90°，AC=3，BC=4，那么下列各式中，正确的是（　　）

A、tanB=　　B、tanA=　C、cosB=　D、cosA=

7、如图将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆洞，最后将正方形纸片展开，得到的图案是（　　 ）

A、　　　　 B、　　　　C、　　　　D、

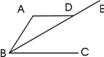
8、如图AD∥BC，若∠ADB=25°，则∠DBC的度数为（　　 ）

A、155°　 B、50°　　C、45°　　D、25°

9、一个箱子中放有红、黄、黑三种小球，三个人先后去摸球，一人摸一次，一次摸出一个小球，摸出后放回，摸出黑色小球为赢，这个游戏是（　 )

A．公平的　　B．不公平的　　C．先摸者赢的可能性大　 D．后摸者赢的可能性大

10、若用（1）（2）（3）（4）四幅图象分别表示变量之间的关系，将下面的（a）（b）（c）（d）对应的图象排序；

（a）面积为定质的矩形；（矩形的相邻两边长的关系）。

（b）运动员推出去的铅球；（铅球的高度与时间的关系）。

（c）一个弹簧不挂重物到逐渐挂重物；（弹簧长度与所挂重物质量的关系）。

（d）某人从A地到B地后，停留一段时间，然后按原速返回；（离开A地的距离与时间的关系）。

其中正确的顺序是（　　）

A、（3）（4）（1）（2）　　B、（3）（2）（1）（4）  C、（4）（3）（1）（2）　　D、（3）（4）（2）（4）

二、填空题（本题有6小题，每小题5分，共30分）

11、温家宝总理在十届全国人大四次会议上谈到解决关于“三农”问题时说，2006年中央财政用于“三农”的支出将达到万元，这个数据用科学工作者记数法可表示为_________万元。

12、反比例函数的图象经过点（-2，1），则=______。

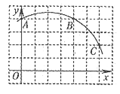
13. 如图所示，直角坐标系中一条圆弧经过网格点A、B、C，其中B点坐标为（4，4），则该圆弧所在圆的圆心坐标为_____________。

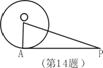14、如图PA是⊙O的切线，切点为A，PA=，∠APO=30°，则⊙O的半径长

为________。

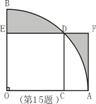15、如图，扇形AOB的圆心角为直角，边长为1的正方形OCDE的顶点，C、E、

D分别在OA、OB、弧AB上，过点A作AF⊥ED，交ED的延长线于点F，则图中阴

影部分的面积S=_________。

16、如图，A是硬币圆周上一点，硬币与数轴相切于原点O（A与O点重合），

假设硬币的直径为1个单位长度。若将硬币沿数轴正方向滚动10周，点A恰

好与数轴上点A´重合，则点A´对应的实数是_______。

三、解答题（本题有8小题）

17、（本题10分）

（1）计算：　　（2）计算：

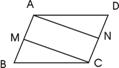
18、（本题8分）已知点M、N分别是平行四边形ABCD的边AB、DC的中点，求证：∠DAN=∠BCM

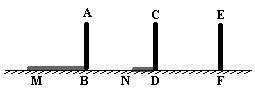
19、（本题8分）电线杆上有一盏路灯O，电线杆与三个等高的标杆整齐划一地排列在马路的一侧，AB、CD、EF是三个标杆，相邻的两个标杆之间的距离都是2 m，已知AB、CD在灯光下的影长分别为BM = 1. 6 m，DN = 0. 6m.

（1）请画出路灯O的位置和标杆EF在路灯灯光下的影子。

（2）求标杆EF的影长。

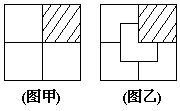
20、（本题8分）如图，把一个正方形割去四分之一，将如下的部分分成3个相同的部分（图甲）；将如下的部分分成4个相同的部分（图乙）。

仿照示例，请你将一个正三角形割去四分之一后余下的部分，

（1）分成3个相同的部分（在图1中画出示意图）；

（2）分成4个相同的部分（在图2中画出示意图）。你还能利用所得的4个相同的部分拼成一个平行四边形吗？若能，画出大致的示意图。

21、（本题10分）

某高科技产品开发公司现有员工50名，所有员工的月工资情况如下表：

员工	管理人员		普通工作人员
人员结构	总经理	部门经理	科研人员	销售人员	高级技工	中级技工	勤杂工
员工数(名)	1	3	2	3		24	1
每人月工资(元)	21000	8400	2025	2200	1800	1600	950

请你根据上述内容，解答下列问题：

为2500元，中位数

为　　　元，众数为　　　元；

（3）小张到这家公司应聘普通工作人员．请你回答

右图中小张的问题，并指出用（2）中的哪个数据向

小张介绍员工的月工资实际水平更合理些；

（4）去掉四个管理人员的工资后，请你计算出其他

员工的月平均工资（结果保留整数），并判断能

否反映该公司员工的月工资实际水平．

22、（本题10分）有一块长为32 m、宽为20 m的矩形鲜花试验基地，准备修筑同样宽的三条直路（如图）把基地分成大小相等的六块作为试验田，种植不同品种的郁金香。要使试验田面积为504 m²，求道路的宽。

 

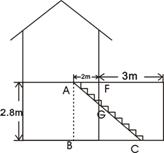
23、（本题12分）小王要装修自己带阁楼的新居（下图为新居剖面图），在建造客厅到阁楼的楼梯AC时，为避免上楼时墙角下碰头，设计墙角F到楼梯的竖直距离FG为1.75m，他量得客厅高AB=2.8m，楼梯洞口宽AF=2m，阁楼阳台宽EF=3m，请你帮助小王解决下列问题：

（1）要使墙角F到楼梯的竖直距离FG为1.75m，楼梯底端C至墙角D的距离CD是多少米？

（2）在（1）的条件下，为保证上楼时的舒适感，楼梯的每个台阶高要小于20cm，每个台阶宽要大于20cm，问小王应该将楼梯建几个台阶？为什么？

E

D

24、（本题14分）如图，已知抛物线，直线经过点B（0，2）。

（1）求的值；

（2）将直线绕着点B旋转到与轴平行的位置时（如图（1）），直线与抛物线相交，其中一个交点为P，求出点P的坐标；

（3）将直线继续绕着点B旋转，与抛物线相交，其中一个交点为P´（如图（2）），过点P´作轴的垂线P´M，点M为垂足，是否存在这样的点P´，使△P´BM为等边三角形？若存在，请求出点P´的坐标；若不存在，请说明理由。