初中毕业生学业数学考试模拟试卷

考生须知：

1．全卷满分为150分，考试时间120分钟．

2．参考公式：二次函数y=ax²+bx+c的顶点坐标是．

温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！

第Ⅰ卷（40分）

一、选择题（本大题共10小题，每小题4分，共40分．下列各题的四个选项中，只有一个选项是符合题意的）

1．如果□，那么“□”内应填的实数是（　　 ）

A．　　　　  B．　　　　 C．　　　　  D．

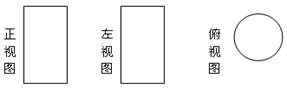2、某物体的三视图是如图所示的三个图形，那么该物体形状是（　 ）

A、长方体　　　B、圆锥体

C、立方体　　　D、圆柱体

3、据《法制日报》2006年6月8日报道，1996年至2004年8年间全国耕地面积减少亩，用科学记数法表示为　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A.1.14×10⁶B.1.14×10⁷ C.1.14×10⁸　　D.0.114×10⁹

4、下列图形中，既是轴对称图形，又是中心对称图形是（　　）

　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　

　　　　 A　　　　　　  B　　　　　　　  C　　　　　　　　　  D　

5、二次函数的图象向上平移2个单位，得到新的图象的二次函数表达式是（　　  ）

A、　　B、　 C、　D、

6． 下图需再添上一个面，折叠后才能围成一个正方体，下面是四位同学补画的情况（图中阴影部分），其中正确的是（　　 ）

 

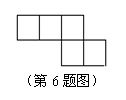
　　　　　　　　　　　  A．　　　　　　  Ｂ．　　　　Ｃ．　　　　　Ｄ．

7．不等式组的解集为(　 )

 A、x>0　　　　 B、x>-　　　 c、-<x<0　　　 　 D、x<0

8．已知⊙O的半径为4㎝，⊙O₁的半径为3㎝，两圆的圆心距为6㎝，则它们的位置关系是(　　)

A、相交　　 B、外切　　 C、相离　　 D、内切

　　 　

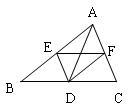
　　 （第9题图）

9．如图，点D、E、F分别是△ABC（AB＞AC）各边的中点，下列说法中，错误的是（　　 ）

A．　　 △DFE是△ABC的位似图形　　 B． EF=BC

C． EF与AD互相平分　　　　　　 D． AD平分∠BAC　　

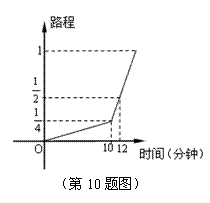
10．一名考生步行前往考场， 10分钟走了总路程的，估计步行不能准时到达，于是他

改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1），则他到达考场所花的时间比一直步行提前了（　　 ）

A．　　 20分钟　 　Ｂ．22分钟　　Ｃ．24分钟　　　　D．26分钟

第Ⅱ卷（110分）

二、填空题（本大题共6小题，每小题5分，共30分．）

11．点P（2，1）关于原点的对称点的坐标是____________

12．下列命题：①对顶角相等； ②等腰三角形的两个底角相等；

③两直线平行，同位角相等．

其中逆命题为真命题的有：　　　　　　 （请填上所有符合题意的序号）．

13．一个函数的图像经过一点（－1，2），请你写出符合上述条件的一种函数关系式 　　　　　　　　　　 。

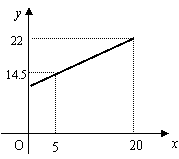
14．右图为弹簧长度y(cm)与所挂物体重量x(kg)之间是一次函数关系的图象，则该弹簧不挂物体时的长度为__________cm.

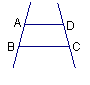15．如图，一个梯形木架，AD=0.5m，BC=0.9m，现要在AD和BC之间均匀地加上三根横木档，做成一个有五阶的木梯，

则新加的三根横木档的总长为__________m。

16． 以下的（1）（2）两题，每个考生只须选答一题，如果两题都答，只以第（2）题计分[第（1）题答对得3分；第（1）题不答，第（2）题答对得5分]．

（1）已知：，，，……，

若 (，为正整数)，请推测=____ __，=___ ___。

（2）小红从A地去B地，以每分钟2米的速度运动，她先前进1米，再后退2米，又前进3米，再后退4米，……依此规律走下去，则1小时后她离A地相距___________米.

三．解答题 （本大题共9小题，共80分）

17．（本题满分8分）

计算：·－(2－π)⁰－()^－1．

18．（本题满分8分）

化简：．

19．（本题满分8分）

　“田忌赛马”是一个有名的历史故事，现设田忌的三匹马分别为，，，他对手的三匹马分别为，，，由故事的内容知，这六匹马的速度从大到小为，假设田忌和他的对手都随意地挑选一匹马参加第一场比赛，则这场比赛有多少种出场情况？请用列表或树状图表示出所有可能出现的结果。并求出田忌获胜的概率是多少？

20．（本题满分8分）

已知：如图，Rt△ABC≌Rt△ADE，∠ABC＝∠ADE=90⁰，试以图中标有字母的点为端点，连结两条线段，如果你所连结的两条线段满足相等、垂直或平行关系中的一种，那么请你把它写出来并加以证明．

　　　　

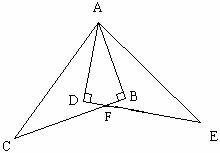
（第20题）　　　　　　　　　　　　　

21．（本题满分10分）

已知：网格中的每个小正方形边长都为1.

（1）将图中的格点△ABC平移，使点A平移至点A′，画出平移后的三角形.

（2）在网格中画一个格点△PQR，使△PQR∽△ABC，且相似比为2∶1.

（第21题）　　　　　　　　　　　　　　　　　  （第22题）

22．(本题满分12分)

如图，AB为⊙O的直径，直线CD切⊙O于点E，BF⊥CD于点F，交⊙O于点M，连结BE.

（1）求证：BE平分∠ABF；

（2）若BF＝8，sin∠EBF＝，求⊙O的半径长.

23．(本题满分12分)

快乐公司决定按左图给出的比例，从甲、乙、丙三个工厂共购买200件同种产品A，已知这三个工厂生产的产品A的优品率如右表所示．

	甲	乙	丙
优品率	80%	85%	90%

 

（1）求快乐公司从丙厂应购买多少件产品Ａ；

（2）求快乐公司所购买的200件产品A的优品率；

（3）你认为快乐公司能否通过调整从三个工厂所购买的产品A的比例，使所购买的200件产品A的优品率上升3%．若能，请问应从甲厂购买多少件产品A；若不能，请说明理由．

24.（本题满分14分）

第一象限内的点A在一反比例函数的图象上，过A作AB⊥轴，垂足为B，连AO，已知

△AOB的面积为4。

（1）　　　 求反比例函数的解析式；

（2）　　　 若点A的纵坐标为4，过点A的直线与轴交于P，且△APB与△AOB相似，求所有符合条件的点P的坐标；

（3）在（2）的条件下，过点P、O、A的抛物线是否可由抛物线平移得到？若是，请说明由抛物线如何平移得到；若不是，请说明理由。