中考数学毕业会考模拟试卷(三)
一、选择题:本大题10个小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、︱-32︱的值是( )
A、-3 B、3 C、9 D、-9
2、下列图形中,是轴对称图形但不是中心对称图形的是( )
A、矩形 B、平行四边形 C、圆 D、等边三角形
3、下列物体中,主视图为图①的是( )
 | |||
 | |||
4、sin30°的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、东方商场把进价为1980元的某商品按标价的八折出售,仍获利10%测该商品的标价为( )
A、2160元 B、2613.6元 C、2640元 D、2722.5元
6、如果一次函数y=kx+b的图象经过点(0,-4)那么b的值是( )
A、1 B、-1 C、-4 D、4
7、数学老师对小明在参加高考前的5次数学模拟考试进行统计分析,判断小明的数学成绩是否稳定,于是老师需要知道小明这5次数学成绩的( )
A、平均数或中位数 B、方差或极差 C、众数或频率 D、频数或众数
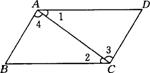
8、如图,∠1=∠2,则下列结论一定成立的是( )
A、AB∥CD B、AD∥BC C、∠B=∠D D、∠3=∠4
(8题图) (9题图) (10题图)
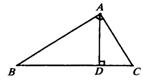
9、如图,在Rt△ABC,CD是斜边AB上的高,则图中的相似三角形共有( )
A、1对 B、2对 C、3对 D、4对
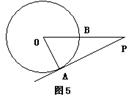
10、如图5,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OA=6,则
tan∠APO的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题:本大题8个小题;每小题3分,共24分.把答案写在题中横线上.
11、据有关资料显示,长江三峡工程电站的总装机容量是千瓦,请你用科学
记数法表示电站的总装机容量,应记为 千瓦
12、分解因式:x2![]() 1=________.
1=________.
13、已知点P(-2,3),则点P关于x轴对称的点坐标是 .
14、抛物线y=![]() 4(x+2)2+5的对称轴是______.
4(x+2)2+5的对称轴是______.
15、若圆的一条弦长为6 cm,其弦心距等于4 cm,则该圆的半径为___.
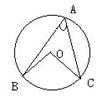 16、如图,在⊙O中,若已知∠BAC=48º,则∠BOC=_________.
16、如图,在⊙O中,若已知∠BAC=48º,则∠BOC=_________.
17、口袋中放有3只红球和11只黄球,这两种球除颜色外没有任何区
 别.随机从口袋中任取一只球,取到黄球的概率是_____.
别.随机从口袋中任取一只球,取到黄球的概率是_____.
18、如图,在梯形 ABCD中,AD∥BC,AB=DC,BD⊥DC
于D,且∠C=60°,若AD=5cm,则梯形的腰长为_____cm.
三、解答题:本大题8个小题;共46分.解答应写出文字说明、证明过程或演算步骤.
19、(每小题5分,共10分)
(1)化简:![]() (2)解方程:
(2)解方程:![]()
20、(5分)如图,∠ACB=90°,DE垂直平分BC,AF=CE.
(1)请你判断四边形AFEC的形状,并说明理由;
(2)猜想:∠F的大小为多少时,四边形AFEC为菱形?
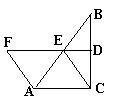 (3)你认为四边形ACEF可能为正方形吗?
(3)你认为四边形ACEF可能为正方形吗?
21、(5分)某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强![]() 是木板面积
是木板面积![]() 的反比例函数,其图象如下图所示.
的反比例函数,其图象如下图所示.
(1)请直接写出这一函数表达式和自变量取值范围;
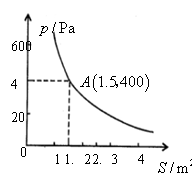 (2)当木板面积为
(2)当木板面积为![]() 时,压强是多少?
时,压强是多少?
(3)如果要求压强不超过![]() ,木板的面积至少要多大?
,木板的面积至少要多大?
22、(5分)已知:如图7,在△ABC中,∠BAC=120°,AB=AC,BC=4![]() ,以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的关系如何?并证明你的结论.
,以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的关系如何?并证明你的结论.

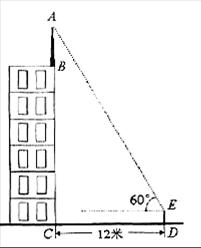 23、(5分)如图.某建筑物BC的楼顶上有一避雷针AB,在距此建筑物12米的D处安置一高度为1.5米的到倾器DE,测得避雷针顶端的仰角为600.又知建筑物共有六层,每层层高为3米.求避雷针AB的长度(结果精确到0.1米).
23、(5分)如图.某建筑物BC的楼顶上有一避雷针AB,在距此建筑物12米的D处安置一高度为1.5米的到倾器DE,测得避雷针顶端的仰角为600.又知建筑物共有六层,每层层高为3米.求避雷针AB的长度(结果精确到0.1米).
(参考数据:![]() )
)
24、(5分)某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,根据下图提供的信息,求一盒“福娃”玩具和一枚徽章的价格各是多少元?
 |
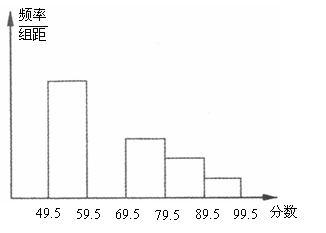
25、(5分)九年级甲、乙两班学生参加电脑知识竞赛,得分均为正整数,将学生成绩进行整理后分成5组,创建频率分布直方图,如图所示,已知图中从左至右的第一、第三、第四、第五小组的频率分别为0.3;0.15;0.1;0.05,且第三小组的频数为6.
(1)求第二小组的频率,并补全频率分布直方图;
(2)求这两个班参赛的学生人数是多少?
(3)这两个班参赛学生成绩的中位数落在第几小组内(不必说明理由).
26、(6分)已知抛物线![]() 的部分图象如图1所示。
的部分图象如图1所示。
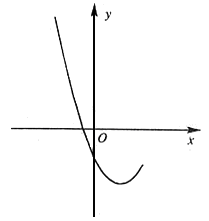
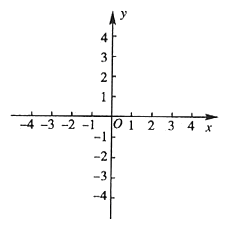
图1 图2
(1)求c的取值范围;
(2)若抛物线经过点(0,-1),试确定抛物线![]() 的解析式;
的解析式;
(3)若反比例函数![]() 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较![]() 与
与![]() 的大小。
的大小。