中考数学操作、设计型专题训练（A）

总分：120分 时间：90分钟

一、细心填一填（每题3分，共30分）

1．在△ABC中，AB>BC>AC，D是AC的中点，过点D作直线z，使截得的三角形与原三角形相似，这样的直线L有　　　 条．

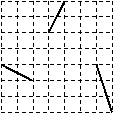
2． （2006年东营）如图，将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形，至少需要移动______________格。

3．（2006年台州）小敏中午放学回家自己煮面条吃．有下面几道工序：①洗锅盛水2分钟；②洗菜3分钟；③准备面条及佐料2分钟；④用锅把水烧开7分钟；⑤用烧开的水煮面条和菜要3分钟．以上各道工序，除④外，一次只能进行一道工序．小敏要将面条煮好，最少用　　　_________分钟．

4．(2006年湖南省郴州)如图，将一副七巧板拼成一只小动物，则　　　　　  ．

　　

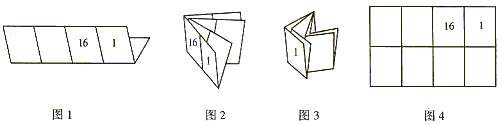
5．(2005年北京海淀) 印刷一本书，为了使装订成书后页码恰好为连续的自然数，可按如下方法操作：先将一张整版的纸，对折一次为4页，再对折一次为8页，连续对折三次为16页，……；然后再排页码. 如果想设计一本16页的毕业纪念册，请你按图1、图2、图3（图中的1，16表示页码）的方法折叠，在图4中填上按这种折叠方法得到的各页在该面相应位置上的页码.

6．（2006年湖南湘西）在一块平地上，张大爷家屋前9米远处有一棵大树．在一次强风中，这棵大树从离地面6米处折断倒下，量得倒下部分的长是10米．出门在外的张大爷担心自己的房子被倒下的大树砸到．大树倒下时能砸到张大爷的房子吗？请你通过计算、分析后给出正确的回答．___________________

7．（2006年荆州）如图的梯形ABCD中，∠A=∠B=90°，且AD=AB，∠C=45°。将它分割成4个大小一样，都与原梯形相似的梯形。（在图形中直接画分割线，不需要说明）

8．（2006年咸宁）在一张长为9cm，宽为8cm的矩形纸片上裁取一个与该矩形三边都相切的圆片后，余下的部分中能裁取的最大圆片的半径为　　　　cm．

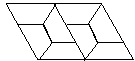
9．（2005年佛山市）如图，是用形状、大小完全相同的等腰提梯形密铺成的图案，则这个图案中的等腰梯形的底角（指锐角）是　　　　 度．

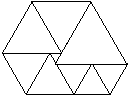
10．（2006年枣庄）右图是由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长是a，则六边形的周长是　　　　　　  .

二、精心选一选（每题3分，共30分）

11．（2005年福州）如图，小亮拿一张矩形纸图（1），沿虚线对折一次得图（2），下将对角两顶点重合折叠得图（3）。按图（4）沿折痕中点与重合顶点的连线剪开，得到三个图形，这三个图形分别是（　　 ）

A．都是等腰梯形　　　　　　　　　　　　　　 B．都是等边三角形

C．两个直角三角形，一个等腰三角形　　　　　 D．两个直角三角形，一个等腰梯形

12．（2006年浙江）Rt△ABC中，斜边AB=4，∠B=60º，将△ABC绕点B旋转60º，顶点C运动的路线长是（　　 ）

A．　　　　　　　　　B．　　　　　　　　 C．　　　　　　　　　 D．　

13．(2006年天门) 如下图a，边长为a的大正方形中一个边长为b的小正方形，小明将图a的阴影部分拼成了一个矩形，如图b。这一过程可以验证　（　　）

A、a²+b²-2ab=(a-b)²　B、a²+b²+2ab=(a+b)²　C、2a²-3ab+b²=(2a-b)(a-b)　D、a²-b²=(a+b) (a-b)

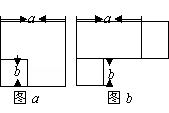
14．（2006年广安）用一把带有刻度尺的直角尺, ①可以画出两条平行的直线a和b, 如图(1); ②可以画出∠AOB的平分线OP, 如图(2); ③可以检验工件的凹面是否为半圆, 如图(3); ④可以量出一个圆的半径, 如图(4).　这四种说法正确的有　 （　　 ）

图(1)　　　　　　  图(2)　　　　　　　 图(3)　　　　　　  图(4)

A. 4个　　　　　　　　　　　　　B. 3个　　　　　　　　　　　　　C. 2个　　　　　　　　　　　　　D. 1个

15．（2006年嘉兴）如图，8×8方格纸上的两条对称轴EF、MN相交于中心点O，对△ABC分别作下列变换：

①先以点A为中心顺时针旋转90°，再向右平移4格、向上平移4格；

②先以点O为中心作中心对称图形，再以点A的对应点为中心逆时针旋转90°；

③先以直线MN为轴作轴对称图形，再向上平移4格，再以点A的对应点为中心顺时针旋转90°．其中，能将△ABC变换成△PQR的是　（　　）

A．①②　　　　　　　　　　　　B．①③　　　　　　　　　　 C．②③　　　　　　　　　　 D．①②③

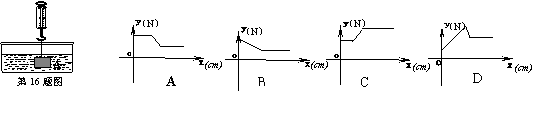
16．（2006年泰州）在物理实验课上，小明用弹簧称将铁块A悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧称的读数y（单位N）与铁块被提起的高度x（单位cm）之间的函数关系的大致图象是（　　  ）

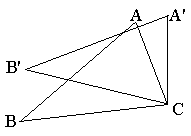
17．如图，将△ABC绕着点C按顺时针方向旋转20°，B点落在位置，A点落在位置，若，则的度数是  （　　  ）

A．50°　　B．60°　  C．70°　　 D．80°

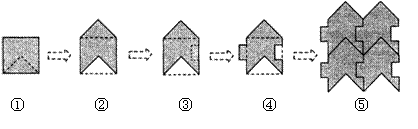18．（2006年吉林）如图，把边长为的正方形的局部进行图①～图④的变换，拼成图⑤，则图⑤的面积是（　　）

Ａ．　　　　　　　　Ｂ．　　　　　　　　Ｃ．　　　　　　　　Ｄ．

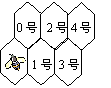19．（2006年舟山）假定有一排蜂房，形状如图，一只蜜蜂在左下角，由于受了点伤，只能爬行，不能飞，而且始终向右方（包括右上、右下）爬行，从一间蜂房爬到右边相邻的蜂房中去.例如，密封爬到1号蜂房的爬法有：蜜蜂→1号；蜜蜂→0号→1号，共有2种不同的爬法.问蜜蜂从最初位置爬到4号蜂房共有几种不同的爬法（　　）

A.7　　　  B.8　　　　C.9　　　  D.10

20．（2006年晋江）如图，将n个边长都为1cm的正方形按如图所示摆放，点A₁、A₂、…、A_n分别是正方形的中心，则n个这样的正方形重叠部分的面积和为（　　）

A．cm²　　　 B．cm² C．cm² D． cm²

三、解答题（每题9分，共45分）

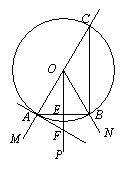
21．（2005年宜昌）小明按下面的方法作出了∠MON的平分线：

①反向延长射线OM；

②以点O为圆心，任意长为半径作圆，分别交∠MON的两边于点Ａ、B，交射线OM的反向延长线于点C；
③连接CB；
④以O为顶点，OA为一边作∠AOP＝∠OCB．

（1）根据上述作图，射线OP是∠MON的平分线吗？并说明理由．

（2）若过点A作⊙O的切线交射线OP于点F，连接AB交OP于点E，当∠MON＝60°、OF＝10时，求AE的长．

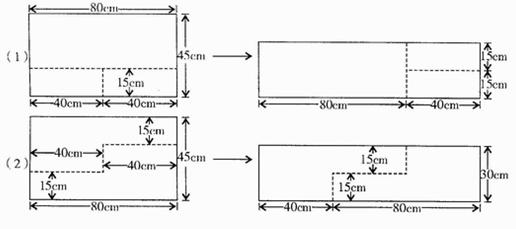
22．（2005年黄冈）蓝天希望学校正准备建一个多媒体教室，计划做长120cm，宽30cm的长条形桌面。现只有长80cm，宽45cm的木板，请你为该校设计不同的拼接方案，使拼出来的桌面符合要求。（只要求画出裁剪、拼接图形，并标上尺寸，设计出一种得4分，设计出两种再加1分）

23．（2005年扬州）若一个矩形的短边与长边的比值为（黄金分割数），我们把这样的矩形叫做黄金矩形。

（1）操作：请你在如图所示的黄金矩形ABCD（AB>AD）中，以短边AD为一边作正方形AEFD；

（2）探究：在（1）中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由；

（3）归纳：通过上述操作及探究，请概括出具有一般性的结论（不需要证明）。

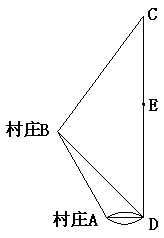
24．（2005年沈阳）如图8所示，A、B为两个村庄，AB、BC、CD为公路，BD为田地，AD为河宽，且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆，共有如下两种铺设方案：

　 方案一：； 方案二：.

经测量得千米，千米，千米，∠BDC＝45°，∠ABD＝15°.

　 已知：地下电缆的修建费为2万元／千米，水下电缆的修建费为4万元／千米.

　 ⑴求出河宽AD（结果保留根号）；

⑵求出公路CD的长；

⑶哪种方案铺设电缆的费用低？请说明你的理由.

25．（2006年连云港）操作与探究：

（1）图①是一块直角三角形纸片。将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕。试证明△CBE等腰三角形；

（2）再将图①中的△CBE沿对称轴EF折叠(如图②)。通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合(指无缝无重叠)所成的矩形，我们称这样的两个矩形为“组合矩形”。你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；

（3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点(各小正方形的顶点)上；

（4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上)。请你进一步探究，一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件是，一定能折成组合矩形？

四、拓广探索（共15分）

26．（2006年柳州、北海）任意剪一个三角形纸片，如图中的△ABC，设它的一个锐角为∠A，首先利用对折的方法得到高AN，然后按图中所示的方法分别将含有∠B、∠C的部分向里折，找出AB、AC的中点D、E，同时得到两条折痕DF、EG，分别沿折痕DF、EG剪下图中的三角形①、②，并按图中箭头所指的方向分别旋转180°。

（1）你能拼成一个什么样的四边形？并说明你的理由；

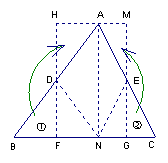（2）请你利用这个图形，证明三角形的面积公式：S＝底×高。

参考答案：

一、填空题

1．2条　2．9格　3．12　 4．135°　

5．

8	9	16	1
5	12	13	4

　

6．若房子高度高于（6－）米，就会被砸中　 7．图略　

8．1

9．60°

10．30a

二、选择题

11．C　 12．B　13．D　 14．A　15．D　 16．C　 17．B　18．B　 19．B　 20．C

三、解答题

21．解：（1）（方法一）∵∠AOF＝∠OCB， 又∵∠BOA＝2∠OCB，

∴∠AOF＝∠BOF…3分∴OP为∠BOA的角平分线

（方法二）∵∠AOF＝∠OCB，∴PO∥BC ，∴∠POB＝∠OBC， 又∵OB=OC，

∴∠OCB＝∠OBC，∴∠AOF＝∠POB，∴OE为∠BOD的角平分线

（2）（方法一）

∵AF与⊙O相切，∴AF⊥AO，

∵∠MON＝60°，∴∠AOF＝∠MON＝30°，

∴AF＝OF＝5，由勾股定理得：AO＝5.

∵AO＝BO，∴△AOB是等腰三角形，∵OP平分∠AOB，∴PO⊥AB，

在Rt△AOF中，S_⊿AOF＝AO×AF＝FO×AE，即：5×5＝10×AE，

∴AE＝

（方法二）∵∠MON＝60°，∴⊿AOB为正三角形，∵OP平分∠MON，

∴AE＝BE＝AB， ，　∵OP平分∠BOD，∴∠BOF＝30°，又∵AF与⊙O相切，∴AF⊥AO　在Rt⊿AOF中，AO＝5，　 ∴AB＝AO＝5，∴AE＝

22．

23．（1）略

 （2）探究：四边形EBCF是矩形，而且是黄金矩形

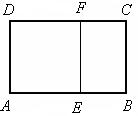∵四边形AEFD是正方形，∴∠AEF=90⁰　 ∴∠BEF=90⁰ ，

∵四边形ABCD是矩形 ，∴∠B=∠C =90⁰　

∴∠BEF=∠B=∠C =90⁰,∴四边形EBCF是矩形

【方法1】设

　∴

∴矩形EBCF是黄金矩形.　

 【方法2】设,　  

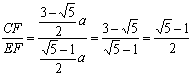 ∴　∴矩形EBCF是黄金矩形

（3）归纳：在黄金矩形内以短边为边作一个正方形后，所得到的另外一个四边形是矩形，而且是黄金矩形(关键词：①另外一个四边形是矩形 ，②是黄金矩形).

24．略

25．（1）∵∠ECB＝90°－∠DCE，∠B＝90°－∠A，又由对称性知，∠A＝∠DCE，∴∠ECB＝∠B，∴△BCE是等腰三角形。

　　

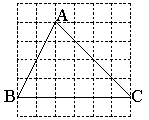
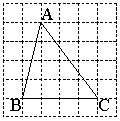
答图1　　　　　　　　　  答图2

（2）如答图1所示（共有三种折法，折痕画对均可）

（3）如答图2所示（答案不唯一，只要体现出一条边与该边上的高相等即可）

（4）当一个四边形的两条对角线互相垂直时，可以折成一个组合矩形。

四、拓展延伸

26．略