中考数学操作、设计型专题训练(B)
总分:120分 时间:90分钟
一、细心填一填(每题3分,共30分)
1.(2005年绍兴)在等式![]() 的两个方格内分别填入一个数,使这两个数是互为相反数且等式成立。则第一个方格内的数是___________
的两个方格内分别填入一个数,使这两个数是互为相反数且等式成立。则第一个方格内的数是___________
2.(2006年舟山)如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是 .

3.(2005年绍兴市)将一副三角板如图1叠放,则左右阴影部分面积![]() :
:![]() 之比等于________,将一副三角板如图2放置,则上下两块三角板面积
之比等于________,将一副三角板如图2放置,则上下两块三角板面积![]() :
:![]() 之比等于________
之比等于________
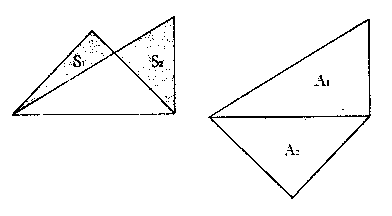
图1 图2
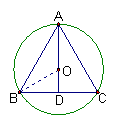
4.(2006年连云港)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm。

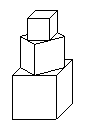
5.(2005年常州)若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,上面正方体的下底四个顶点是下面相邻正方体的上底各边中点,最下面的正方体棱长为1,如果塔形露在外面的面积超过7,则正方体至少__________个。
6.(2006年临安)用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC= 度.


7.(2006年永州)如图所示为农村一古老的捣碎器,已知支撑柱![]() 的高为 0.3米,踏板
的高为 0.3米,踏板![]() 长为1.6米,支撑点
长为1.6米,支撑点![]() 到踏脚
到踏脚![]() 的距离为0.6米,现在踏脚着地,则捣头点
的距离为0.6米,现在踏脚着地,则捣头点![]() 上升了
_________米.
上升了
_________米.

8.(2006年南昌市)请在由边长为1的小正三角形组成的虚线网格中,画出1 个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形
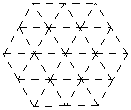
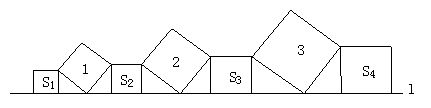
9.在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_________
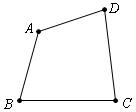
10.(2006年天津)如图,已四边形纸片ABCD,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到:__________(用“能”或“不能”填空)。若填“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由______________________________________________________________________
____________________________________________________________________________
_____________________________________________________________________________
二、精心选一选(每题3分,共30分)
11.(2006年绍兴)时是电视机常用规格之一,1时约为拇指上面一节的长,则7时长相当于( )
A.课本的宽度 B.课桌的宽度 C.黑板的高度 D.粉笔的长度
12.(2006年诸暨提前招生)如果从一卷粗细均匀的电线上截取1米长的电线, 称得它的质量为![]() 克,再称得剩余电线的质量为
克,再称得剩余电线的质量为![]() 克, 那么原来这卷电线的总长度是 ( )
克, 那么原来这卷电线的总长度是 ( )
A.米 B.(+1)米 C.(+1)米 D.(+1)米
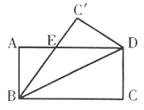
13.(2005年内江市)如图,将矩形ABCD沿对角线BD折叠,使C落在C'处,BC'交AD于E,则下列结论不一定成立的是( )
A.AD=BC' B.∠EBD=∠EDB C.△ABE∽△CBD D.![]()
14.(2006年天门)将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是
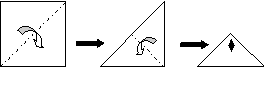



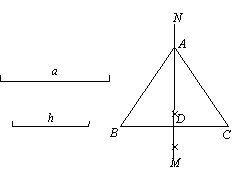
15.(2006年益阳)如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h. 张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连结AB,AC,△ABC为所求的等腰三角形. 上述作法的四个步骤中,有错误的一步你认为是
A. (1) B. (2) C. (3) D. (4)
 |
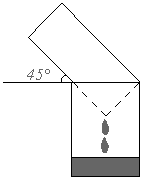
16(2006年长春)如图,将圆桶中的水倒入一个直径为40cm,高为55cm的圆口容器中,圆桶放置的角度与水平线的夹角为45o.若使容器中的水与圆桶相接触,则容器中水的深度至少应为 ( )
A.10cm. B.20cm. C.30cm. D.35cm.
17.(2006年盐城)在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成三角形,又能拼成平行四边形和梯形的可能是( )

18.(2006年茂名)如图,小明想用皮尺测最池塘A、B间的距离,但现有皮尺无法直接测量,学习数学有关知识后,他想出了一个主意:先在地上取一个可以直接到达A、B两点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD = a,由此他即知道A、B距离是 ( )
A.![]() B.2a C.a
D.3a
B.2a C.a
D.3a

19.(2005年荆州市)如图,王虎使一长为4![]() ,宽为3
,宽为3![]() 的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为
的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为![]() ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.10![]() B.
B.![]() C.
C.![]() D.
D.![]()
 |
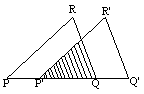
20.(2006年杭州)如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=![]() ,则此三角形移动的距离PP′是
,则此三角形移动的距离PP′是
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
三、解答题(每题9分,共45分)
21.(2006年浙江)现有一张长和宽之比为2:1的长方形纸片,将它折两次(第一次折后也可打开铺平再者第二次),使得折痕将纸片分为面积相等且不重叠的四个部分(称为一次操作),如图甲(虚线表示折痕).
除图甲外,请你再给出三种不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作,如图乙和图甲示相同的操作).
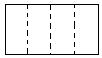
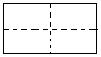



甲 乙 ① ② ③
22.(2006年伊春) 如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点D顺时针方向旋转900,1800,2700的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为l,旋转后点A的对应点依次为A1、A2、A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.

23.(2005年徐州)如图,AC是平行四边形ABCD的对角线。
 (1)用直尺和圆规作AC的垂直平分线和边AD、BC分别相交于点E、F,垂足为O。连结AF、CE(保留作图痕迹,不写作法)
(1)用直尺和圆规作AC的垂直平分线和边AD、BC分别相交于点E、F,垂足为O。连结AF、CE(保留作图痕迹,不写作法)
(2)判断四边形AFCE是否为菱形,并说明理由。

24.(2005年扬州)若一个矩形的短边与长边的比值为![]() (黄金分割数),我们把这样的矩形叫做黄金矩形。
(黄金分割数),我们把这样的矩形叫做黄金矩形。
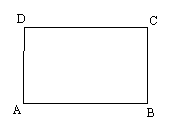
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由;
(3)归纳:通过上述操作及探究,请概括出具有一般性的结论(不需要证明)。
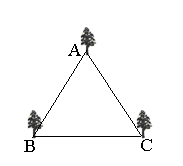
25.(2005年丽水) 某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.
 | |||
 | |||
| |||
| |||
四、拓广探索(共15分)
26 (2006年河北) 在图1至图3中,已知△ABC的面积为a .
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=______(用含a的代数式表示);
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2=__________(用含a的代数式表示);
(3)在图12—2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=__________(用含a的代数式表示),并运用上述(2)的结论写出理由.






发现
像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 倍.
应用
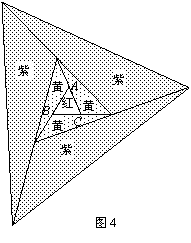
要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4)已给出了前两次扩展的图案).在第一次扩展区域内种黄花,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:
(1)种紫花的区域的面积;
(2)种蓝花的区域的面积.
|

参考答案:
一、填空题
1.3 2.三角形的稳定性 3.![]() ,
,![]() 4.
4.![]() 5.3个 6.36° 7.0.8
5.3个 6.36° 7.0.8
8.本题答案不惟一,只要符合要求都给满分,以下答案供参考

9.4
10.无数。例如,过点C作与AB平行的直线将该五边形分割为一个矩形和一个梯形,经过梯形中位线的中点及矩形对角线的交点的直线可将该五边形的面积均分;设该直线与边DE、AB的交点分别为P、Q,线段PQ的中点为O,则经过点O且与边DE、AB相交的任意一条直线均可将该五边形的面积均分。
二、选择题
11.A 12.B 13.C 14.C 15.C 16.D 17.C 18.B 19.C 20.A
三、解答题
21.
22.(1)如图,正确画出图案

(2)如图,![]() =
=![]() -4
-4![]()
=(3+5)2-4××3×5
=34
故四边形似AA1A2A3的面积为34.
(3)结论:AB2+BC2=AC2或勾股定理的文字叙述
23.∵直径AB垂直于弦CD,∴AD=AC,∴∠AEC=∠ACF
又∵∠EAC=∠FAC,∴△AEC∽△ACF
∴![]() ,又∵
,又∵![]() ,∴
,∴![]()
又∵CF=10,∴CE=8
24.(1)略
(2)探究:四边形EBCF是矩形,而且是黄金矩形
 ∵四边形AEFD是正方形,∴∠AEF=900 ∴∠BEF=900 ,
∵四边形AEFD是正方形,∴∠AEF=900 ∴∠BEF=900 ,
∵四边形ABCD是矩形 ,∴∠B=∠C =900
∴∠BEF=∠B=∠C =900,∴四边形EBCF是矩形
【方法1】设![]()
∴![]()
∴矩形EBCF是黄金矩形.
【方法2】设![]() ,
, ![]()
∴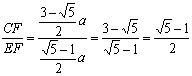 ∴矩形EBCF是黄金矩形
∴矩形EBCF是黄金矩形
(3)归纳:在黄金矩形内以短边为边作一个正方形后,所得到的另外一个四边形是矩形,而且是黄金矩形(关键词:①另外一个四边形是矩形 ,②是黄金矩形).
25.解:(1)作图工具不限,只要点A、B、C在同一圆上;
|
(3)∵r=OB=![]() =
=![]() ,
,
∴S⊙O=![]() r2=
r2=![]() ≈16.75,
≈16.75,
又S平行四边形=2S△ABC=2×![]() ×42×sin60º=8
×42×sin60º=8![]() ≈13.86,
≈13.86,
∵S⊙O > S平行四边形 ∴选择建圆形花坛面积较大.
四、拓展延伸
26.探索(1)a ;(2)2a ;(3)6a ;
理由:∵CD=BC,AE=CA,BF=AB
∴由(2)得 S△ECD=2a,S△FAE=2a,S△DBF=2a,
∴S3=6a
发现 7.
应用 (1)(72-7)×10=420(平方米); (2)(73-72)×10=2940(平方米).