九年级数学联考试卷
姓名 考号 班级 得分
一、选择题(本题共有11个小题,每小题3分,共33分)在每个小题给出的四个备选答案中,只有一个是符合题意的
1.刘翔在出征雅典奥运会前刻苦进行110米跨栏训练,教练对他10次的训练成绩进行统计分析,判断他的成绩是否稳定,则教练需要知道刘翔这10次成绩的( )
A.众数 B.方差 C.平均数 D.频数
2.光年是天文学中的距离单位,1光年约是km,用科学计数法表示为( )
(A)![]() km (B)
km (B)![]() km (C)
km (C)![]() km (D)
km (D)![]() km
km
3. 如图是由5个大小相同的正方体摆成的立方体图形,它的左视图是( )
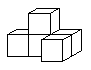
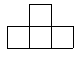
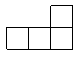
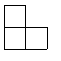
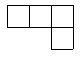
(A) (B) (C) (D)
4. 等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的有( )
(A)1个 (B)2个 (C)三个 (D)四个
5. 下列运算正确的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
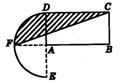 6. 设计一个商标图案:先作矩形ABCD,使AB=2BC,AB=8,再以点A为圆心、AD的长为半径作半圆,交BA的延长线于F,连FC. 图中阴影部分就是商标图案,该商标图案的面积等于( )
6. 设计一个商标图案:先作矩形ABCD,使AB=2BC,AB=8,再以点A为圆心、AD的长为半径作半圆,交BA的延长线于F,连FC. 图中阴影部分就是商标图案,该商标图案的面积等于( )
(A)4![]() +8;(B)4
+8;(B)4![]() +16;
+16;
(C)3![]() +8;(D)3
+8;(D)3![]() +16
+16
7. 若方程组![]() 的解是
的解是![]() ,则k的取值是( )
,则k的取值是( )
A.-4 B.-5 C.-8 D.-6
8. 由小到大排列一组数据x![]() ,x
,x![]() ,x
,x![]() ,x
,x![]() ,x
,x![]() ,其中每个数据都小于-1,则对于样本1,x
,其中每个数据都小于-1,则对于样本1,x![]() ,-x
,-x![]() ,x
,x![]() ,-x
,-x![]() ,x
,x![]() 的中位数是( )
的中位数是( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
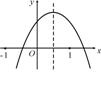
9. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,
给出以下结论:① a+b+c<0;② a-b+c<0;③ b+2a<0;
④ abc>0 . 其中所有正确结论的序号是 ( )
A. ③④ B. ②③ C. ①④ D. ①②③
10. 如图,在□ABCD中,EF∥AB,DE∶EA=2∶3,若EF=4,则CD的长为( )
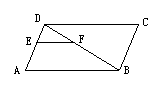 (A) (B) 8
(A) (B) 8
(C) 10 (D)16
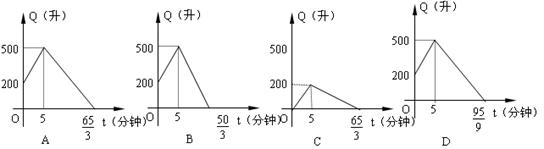
11. 有一个装有进、出水管的容器,单位时间内进、出的水量都是一定的。已知容器的容积为600升,又知单开进水管10分钟可把空容器注满,若同时打开进、出水管,20分钟可把满容器的水放完,现已知水池内有水200升,先打开进水管5分钟后,再打开出水管,两管同时开放,直至把容器中的水放完,则能正确反映这一过程中容器的水量Q(升)随时间t(分)变化的图象是( )
 二、填空题(本大题共5小题,每小题4分,满分20分)
二、填空题(本大题共5小题,每小题4分,满分20分)
12. .函数y= 中,自变量x的取值范围是 .
13. 用换元法解分式方程+= 7时,如果设y = ,那么原方程可化为关于y的一元二次方程的一般形式是 .
14. 关于x的不等式3x-2a≤-2的解集如图所示,则a的值是 .
![]()
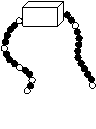
15. 一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分
(如图),则这串珠子被盒子遮住的部分有___ 颗.
16. 已知![]() ,则分式
,则分式![]() 的值为_________.
的值为_________.
三.解答题。(本题共4小题,每小题6分。共24分)
17. 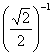 -
-![]() +2sin45
+2sin45![]() -cos60
-cos60![]() +
+![]()
18. 解方程:-=2
19. 已知![]() 。试说明不论x为何值,y的值不变
。试说明不论x为何值,y的值不变
20. 解方程:![]() (公式法解)
(公式法解)
四.解答题。(本题共3小题,每小题7分。共21分)
21. 小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判。
⑴你认为游戏公平吗?为什么?
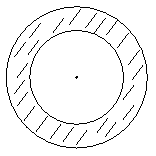 ⑵游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算非规则图形的面积呢?”。请你设计方案,解决这一问题。(要求画出图形,说明设计步骤、原理,写出公式)
⑵游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算非规则图形的面积呢?”。请你设计方案,解决这一问题。(要求画出图形,说明设计步骤、原理,写出公式)
22. 如图,一天晚上,李杨在广场上乘凉. 图中线段AB表示站在广场上的李杨,线段PO表示直立在广场上的灯杆,点P表示照明灯.
⑴请你在图中画出李杨在照明灯(P)照射下的影子;
⑵如果灯杆高PO=12m,李杨的身高AB=1.6m,李杨与灯杆的
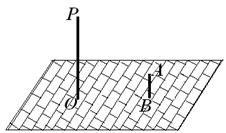 距离BO=13m,请求出李杨影子的长度.
距离BO=13m,请求出李杨影子的长度.
解:
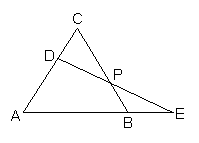 23. 如图,正三角形ABC的边长为2,D为AC边上的一点,延长AB至点E,使BE=CD,连结DE,交BC于点P。
23. 如图,正三角形ABC的边长为2,D为AC边上的一点,延长AB至点E,使BE=CD,连结DE,交BC于点P。
(1)求证:DP=PE;
(2)若D为AC的中点,求BP的长。
 五.解答题。(本题共2小题,每小题7分。共14分)
五.解答题。(本题共2小题,每小题7分。共14分)
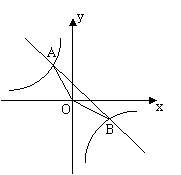
24. 如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;
(2)⊿AOB的面积.
25. 如图,A是⊙O外一点,B是⊙O上一点,AO的延长线交⊙O于点C,连结BC,∠C=22.5°,∠A=45°.
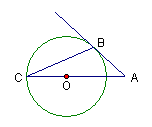 求证:直线AB是⊙O的切线.
求证:直线AB是⊙O的切线.
六.解答题。(本题8分)
二次函数![]() 的图象以过点A(3,0)、B(2,-3),并且以
的图象以过点A(3,0)、B(2,-3),并且以![]() 为对称轴。
为对称轴。
(1)求此函数的解析式;
(2)在给出的坐标系中作出此二次函数的大致图象;
 (3)以对称轴
(3)以对称轴![]() 上是否存在一点P,使△PAB中PA=PB,若存在,求出P点的坐标,若不存在,主说明理由。
上是否存在一点P,使△PAB中PA=PB,若存在,求出P点的坐标,若不存在,主说明理由。