九年级数学素质调研卷(一)
班级 姓名 得分
一、选择题(本题有10小题,每小题4分,共40分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1. 计算-1-(-5)的结果是【 】
(A)-6 (B)4 (C) 6 (D)-4
2. 9的算术平方根是 【 】
![]() (A)±3 (B)
(A)±3 (B)![]() (C)3 (D)-3
(C)3 (D)-3
3. 光年是天文学中的距离单位,1光年约是km,用科学计数法表示为【 】
(A)![]() km (B)
km (B)![]() km (C)
km (C)![]() km (D)
km (D)![]() km
km
4.已知点P(m,-n)和点Q(-m,n),那么点P和点Q 【 】
(A)关于x轴对称 (B)关于y轴对称
(C)关于原点对称 (D)以上结论都不对
5. 下列计算中不正确的是 【 】
(A)(-2)0=1 (B)2-1=-2 (C)(a+b)2=a2+2ab+b2 (D)2a2·3a3=6a5
6.函数y=![]() 中,自变量x的取值范围是【 】
中,自变量x的取值范围是【 】
(A)x>-2且x≠1 (B)x≥2且x≠1 (C)x≥-2且x≠1 (D)x≠1
7.当![]() ,
,![]() 时,
时,![]() 的图象经过 【 】
的图象经过 【 】
(A) 第1、2、3象限 (B) 第2、3、4象限
(C) 第1、2、4象限
(D) 第1、3、4象限
 8. 右边给出的是2006年3月份的日历表,任意
8. 右边给出的是2006年3月份的日历表,任意
圈出一竖列上相邻的三个数,请你运用方程思想来研
究,发现这三个数的和不可能是【 】
(A) 69 (B) 54 (C) 27 (D)40
9.二次函数![]() 的图像与
的图像与![]() 图像的形状、开口方向相同,只是位置不同,
图像的形状、开口方向相同,只是位置不同,
则二次函数![]() 的顶点坐标是【
】
的顶点坐标是【
】
(A) (![]() ) (B)
(
) (B)
(![]() )
(C) (
)
(C) (![]() ) (D) (
) (D) (![]() )
)
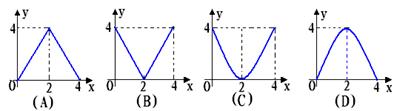
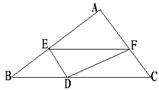 10. 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC边上一个 动点,EF∥BC,交AB于点E,交AC于点F,设E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致为【 】
10. 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC边上一个 动点,EF∥BC,交AB于点E,交AC于点F,设E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致为【 】
二、填空题(本题有6小题,每小题5分,共30分)
11. 如果m与-2互为倒数,那么m的值是 .
12. 把x2+9加上一个单项式,使其成为一个完全平方式.请你写出1个符合条件
的单项式 .
13.用换元法解分式方程+= 7时,如果设y = ,那么原方程可化为关于y的一元二次方程的一般形式是 .
14.关于x的不等式3x-2a≤-2的解集如图所示,则a的值是 .
![]()
15.分解因式:
![]() =
.
=
.
16.小明背对小亮,让小亮按下列四个步骤操作:
第一步 分发左、中、右三堆牌,每堆牌不少于3张,且各堆牌现有的张数相同;
第二步 从左边一堆拿出3张,放入中间一堆;
第三步 从右边一堆拿出2张,放入中间一堆;
第四步 左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是 * .
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
17. 分解因式:16-x2-y2+2xy.
18. 计算:![]()
19. 用换元法解方程 ![]() .
.
20.已知![]() 。试说明不论x为何值,y的值不变。
。试说明不论x为何值,y的值不变。
21. 列方程或方程组解应用题:
为加快农村小城镇建设,某镇经过规划设计,有80万平方米的街道和空地需要改造和绿化,如果街道铺设柏油和空地绿化面积各占50%,则需要投资30万元,如果街道铺设柏油占40%,空地绿化占60%,则需要投资28万元,问每铺设街道柏油和空地绿化1万平方米各需要投资多少万元?
22. 已知:关于x的两个方程x2+(m+1)x+m-5=0……①与mx2+(n-1)x+m-4=0…②,
方程①有两个不相等的负实数根,方程②有两个实数根.
(1)求证方程②的两根符号相同;
(2)设方程②的两根分别为α、β,若α ∶β=1∶3, 且n为整数,求m的最小整数值.
23. 某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、
清洗、排水时洗衣机中的水量![]() (升)与时间
(升)与时间![]() (分钟)之间的关系如折线图所示:
(分钟)之间的关系如折线图所示:
 根据图象解答下列问题:
根据图象解答下列问题:
(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(2)已知洗衣机的排水速度为每分钟19升,
① 如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量。
②求排水时y与x之间的函数关系式,并写出![]() 的取值范围.
的取值范围.
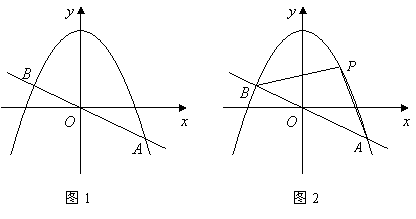
24、如图1,已知直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求线段![]() 的垂直平分线的解析式;
的垂直平分线的解析式;
(3)如图2,取与线段![]() 等长的一根橡皮筋,端点分别固定在
等长的一根橡皮筋,端点分别固定在![]() 两处.用铅笔拉着这根橡皮筋使笔尖
两处.用铅笔拉着这根橡皮筋使笔尖![]() 在直线
在直线![]() 上方的抛物线上移动,动点
上方的抛物线上移动,动点![]() 将与
将与![]() 构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时
构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时![]() 点的坐标;如果不存在,请简要说明理由.
点的坐标;如果不存在,请简要说明理由.