九年级数学学业水平检测试卷
满分 150分 考试时间 120分钟
参考公式:二次函数y=ax2+bx+c的顶点坐标是![]()
一、选择题(本题共10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选均不给分)
1.下列实数中,属于无理数的是( )
A、0 B、![]() C、
C、![]() D、-3
D、-3
2.下列四个数据中,准确数是( )
A、九(1)班有48名同学 B、数学书的长度为21.0cm
C、印尼海啸伤亡10万人 D、3月8日比3月7日气温低6℃。
3.十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒。当你抬头看信号灯时,看到黄灯的概率是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4.若点P(![]() )在第二象限,则下列关系中正确的是( )
)在第二象限,则下列关系中正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5. 2006年世界杯足球赛在德国慕尼黑举行,共有32支球队参赛,分为8个小组,按规则在第一轮比赛中组内4个球队之间相互都要进行一场比赛。那么第一轮比赛全部结束后,32支球队之间相互进行的比赛总场数( )
2006年世界杯足球赛在德国慕尼黑举行,共有32支球队参赛,分为8个小组,按规则在第一轮比赛中组内4个球队之间相互都要进行一场比赛。那么第一轮比赛全部结束后,32支球队之间相互进行的比赛总场数( )
A、64 B、48 C、32 D、16
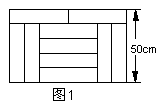
6. 如图1,宽为50cm的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为(
)
如图1,宽为50cm的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为(
)
A、4000cm2 B、500 cm2 C、600 cm2 D、400 cm2
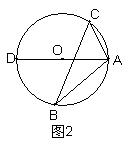
7.如图2,△ABC内接于⊙O,AD是⊙O的直径,
∠ABC=30°。则∠CAD等于( )
A、30° B、40° C、50° D、60°
8.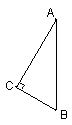 将右图所示放置的Rt△ABC(∠C=90°)绕斜边AB旋转一周,
将右图所示放置的Rt△ABC(∠C=90°)绕斜边AB旋转一周,
所得到的几何体的主视图是下面四个图形中的( )
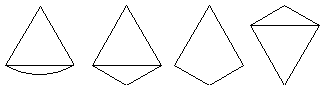
A B C D
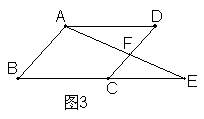
9.如图3,点E是□ABCD的边BC延长线上的点,AE与CD相交于点F,则图中相似三角形共有( )
A、2对 B、3对 C、4对 D、5对
 | |||
 | |||
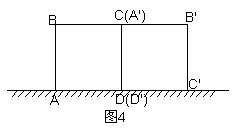
10. 如图4,一块边长为10cm的正方形木板ABCD,在水平桌面上绕点D按顺时针方向旋转到![]() 位置时,顶点B从开始到结束所经过的路径为
位置时,顶点B从开始到结束所经过的路径为
( )
A、20cm B、![]() C、
C、![]() cm D、
cm D、![]() cm
cm
二、填空题 (本题有6小题,每题5分,共30分)
11.
 据中新网报道,2006年我国的国内生产总值达到210000亿元,请将这一数据用科学记数法表示为
亿元。
据中新网报道,2006年我国的国内生产总值达到210000亿元,请将这一数据用科学记数法表示为
亿元。
12. 函数![]() 中自变量x的取值范围是
。
中自变量x的取值范围是
。
13. 因式分解:![]() =
。
=
。
14.
 如图5,一个顶角为30°的等腰三角形纸片,剪去顶角后,得到一个四边形,则∠1+∠2=
°
如图5,一个顶角为30°的等腰三角形纸片,剪去顶角后,得到一个四边形,则∠1+∠2=
°
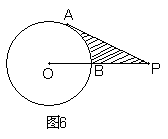
15. 如图6,PA切⊙O于点A,OP交⊙O于点B,若PB=1,PA=![]() ,则图中阴影部分的面积S=
。
,则图中阴影部分的面积S=
。
16.
瑞士中学教师巴尔末成功地从光谱数据![]() 中得到巴尔末公式,从而打开了光谱奥妙的大门,请你按这种规律写出第8个数据是
。
中得到巴尔末公式,从而打开了光谱奥妙的大门,请你按这种规律写出第8个数据是
。
三、解答题 (本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
17. (本题有2小题,每题4分)
(1) 计算:![]()
(2) 解方程:![]()
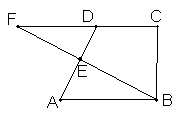
18. 如图,已知四边形ABCD是梯形,AB∥CD,E是AD的中点,BE的延长线与 CD的延长线交于点F。求证:AB=DF
19. 某校为了了解学生环保情况,对部分学生进行了一次环保知识测试(分数为整数,满分100分),根据测试成绩(最低分53分)分别绘制如下统计表和统计图,请你根据统计表和统计图回答下列问题:
| 分数 | 59.5分以下 | 59.5分以上 | 69.5分以上 | 79.5分以上 | 89.5分以上 |
| 人数 | 3 | 42 | 32 | 20 | 8 |
(1) 这次参加测试的总人数为 人。
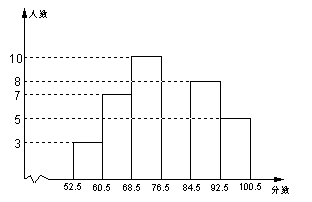
(2) 请补全频数分布直方图。
(3) 这次测试成绩的中位数落在直方图的哪个小组内?
答: 。
(4) 成绩在84.5~89.5之间的人数是 人。
20. 用四个如图1的直角三角形(两直角边长分别为 a、b,斜边长为c),拼成如图2的四边形ABCD。
(1)发现四边形ABCD是什么特殊四边形?答: 。
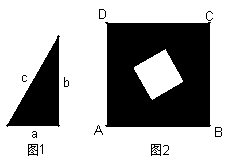 (2)利用这个图形你还能发现什么结论(或定理)?试证明这个结论(或定理)。
(2)利用这个图形你还能发现什么结论(或定理)?试证明这个结论(或定理)。
结论(或定理): 。
证明:
21. 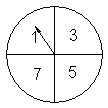 在公园前有一摆摊人,他面前放一个如图所示的4等份转盘,呼叫过路人来玩游戏,并规定:玩的人每人交5元,可转动两次转盘(指针压界重转一次),获奖方法是:
在公园前有一摆摊人,他面前放一个如图所示的4等份转盘,呼叫过路人来玩游戏,并规定:玩的人每人交5元,可转动两次转盘(指针压界重转一次),获奖方法是:
①两次指针都指向7时,玩者可获奖10元;
②两次中有一次指针指向7,玩者可获奖5元;
③两次指针都不指向7时,若指针所指数字之和大于7。则玩
者可获奖为两数之和与7的差是几就是几元(如5+3-7=1获奖1元)
④其余情况无奖,请回答下列问题。
(1) 利用画树状图或列表法,分别求出玩者可获奖金10元的概率与玩者无奖的概率;
(2) 按照这种概率预计,若有32人参加这个游戏(每人玩一次),摊主是赔还是赚?赔或赚多少?
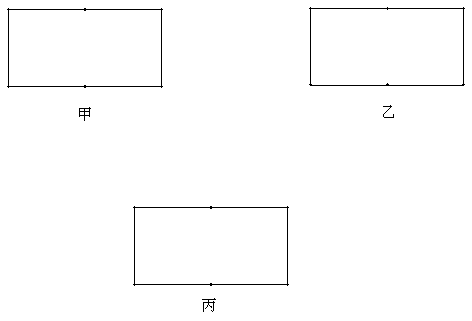
22. 如图有一矩形纸片,已知长是宽的2倍。把这个矩形分别剪成:
(1) 两部分,使得能用它们拼成一个等腰三角形(图甲);
(2) 两部分,使得能用它们拼成一个等腰梯形(图乙)
(3) 三部分,使得能用它们拼成一个正方形(图丙)
请按上述要求在对应图中画出拼成图形的示意图。
23. 镇政府为绿化一段沿江风光带,计划购买甲、乙两种树苗共500株,甲种树苗每株50元,乙种树苗每株80元.有关统计表明:甲、乙两种树苗的成活率分别为90%和95%.
(1) 若购买树苗共用了28000元,求甲、乙两种树苗各多少株?
(2) 若购买树苗的钱不超过34000元,应如何选购树苗?
(3) 若希望这批树苗的成活率不低于92%,且购买树苗的费用最低,应如何选购树苗?
24. 如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s)。
(1) 求x为何值时,PQ⊥AC;
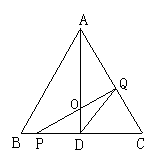
(2) 当0<x<2时,求证:AD平分△PQD的面积;
(3) ①设△PQD的面积为y(cm2),求y与x的函数关系式,及自变量x的取值范围;
②△PQD的面积是否有最大值?若有,请求出这个最大值,及此时x的值;若没有,请说明理由.
