第二节 频率与概率
【回顾与思考】

【例题经典】
能够理解用试验得到的频率当作概率用
例1 (2006年成都市)含有4种花色的36张扑克牌的牌面都朝下,每次抽出一张记下花色后再原样放回,洗匀牌后再抽.不断重复上述过程,记录抽到红心的频率为25%,那么其中扑克牌花色是红心的大约有________张.
【点评】频率为25%,就作为概率即36×25%=9(即可)
能够根据实际情况制作模拟试验
例2 你几月份过生日?和同学交流,看看6个同学中是否有2个人同月过生日,开展调查,看看6个月中2个人同月过生日的概率大约是多少?
【点评】以12月份为号码编球或用计算器作模拟试验.
能借助用频率估计理论概念的方法解决问题
例3 (2006年临安市)为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合鱼群中以后,再捕捞200条,若其中有标记的鱼有10条,则估计池塘里有鱼________条.
【点评】这种方法本身就是一种估算,不能说它是一种准确值.
【考点精练】
一、基础训练
1.某市对2400名年满15岁的男生的身高进行了测量,结果身高(单位:m)在1.68~1.70这一小组的频率为0.25,则该组的人数为( )
A.400人 B.150人 C.60人 D.15人
 2.(2006年河南省)有一个不透明的布袋中,红色、黑色、白色的玻璃共有40个,除颜色外其它完全相同.小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( )
2.(2006年河南省)有一个不透明的布袋中,红色、黑色、白色的玻璃共有40个,除颜色外其它完全相同.小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( )
A.6 B.16 C.18 D.24
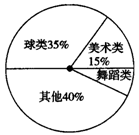
3.(2006年常德市)右图是某中学七年级学生参加课外活动人数的扇形统计图,若参加舞蹈类的学生有42人,则参加球迷活动的学生人数有( )
A.145 B.147 C.149 D.151
4.甲、乙、丙、丁四名运动员参加4×100米接力赛,甲必须为第一接力棒或第四接棒的运动员,那么这四名运动员在比赛过程的接棒顺序有( )
A.3种 B.4种 C.6种 D.12种
 5.(2006年青岛市)一个口袋中有12个白球和若干个黑球,在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下方法:每次先从口袋中摸出10个球,求出其中白球数与10的比值,再把球放回口袋中摇匀.不断重复上述过程5次,得到的白球数与10的比值分别为:0.4,0.1,0.2,0.1,0.2,根据上述数据,小亮可估计口袋中大约有_______个黑球.
5.(2006年青岛市)一个口袋中有12个白球和若干个黑球,在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下方法:每次先从口袋中摸出10个球,求出其中白球数与10的比值,再把球放回口袋中摇匀.不断重复上述过程5次,得到的白球数与10的比值分别为:0.4,0.1,0.2,0.1,0.2,根据上述数据,小亮可估计口袋中大约有_______个黑球.
6.(2006年温州市)右图是由8块相同的等腰直角三角形黑白瓷砖镶嵌而成的正方形示意图,一只蚂蚁在上面自由爬动,并随机停留在某块瓷砖上,蚂蚁留在黑色瓷砖上的概率是_______.
7.在一个有10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻,在该镇随便问一个人,他看早间新闻的概率大约是________.
8.某口袋中有红色、黄色、蓝色玻璃球共72个.小明通过多次摸球试验后,发现摸到红球、黄球、蓝球的概率依次是35%,25%和40%,试估计口袋中三种玻璃球的数目依次是______.
9.(2006年泉州市)在一个不透明的箱子里放有除颜色外,其余都相同的4个小球,其中红球有3个、白球1个.搅匀后,从中同时摸出2个小球,请你写出这个实验中的一个可能事件:_________.
二、能力提升
10.(2006年河南省)一枚均匀的正方体骰子,六个面分别标有数字1,2,3,4,5,6,连续抛掷两次,朝上的数字分别是m,n.若把m,n作为点A的横、纵坐标,那么点A(m,n)在函数y=2x的图象上的概率是多少?
11.(2006年大连市)在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是![]() .
.
(1)试写出y与x的函数关系式.
(2)若往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为![]() ,求x和y的值.
,求x和y的值.
12.有2个信封,每个信封内各装有四张卡片,其中一个信封内的四张卡片上分别写有1,2,3,4四个数,另一个信封内的四张卡片上分别写出5,6,7,8四个数,甲、乙两人商定了一个游戏,规则是:从这两个信封中各随机抽取一张卡片,然后把卡片上的两个数相乘,如果得到的积大于20,则甲获胜,否则乙获胜.
(1)请你通过列表(或画树状图)计算甲获胜的概率;
(2)你认为这个游戏公平吗?为什么?
13.(2006年泉州市)在两个布袋中分别装有三个小球,这三个小球的颜色分别为红色、白色、绿色,其他没有区别,把两袋小球都搅匀后,再分别从两袋中各取出一个小球,试求取出两个相同颜色小球的频率(要求用树状图或列表方法求解).
14.(2006年遂宁市)将分别标有数字2,3,5的三张质地,大小完全一样的卡片背面朝上放在桌面上.
(1)随机抽取一张,求抽到奇数的概率;
(2)随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并求出抽取到的两位数恰好是35的概率.
三、应用与探究
15.(2006年扬州市)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近_______;
(2)假如你去摸一次,你摸到白球的概率是________,摸到黑球的概率是_______;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
(4)解决了上面的问题,小明同学猛然顿悟,过去一个悬而未决的问题有办法了.这个问题是:在一个不透明的口袋里装有若干个白球,在不允许将球倒出来数的情况下,如何估计白球的个数(可以借助其他工具及用品)?请你应用统计和概率的思想和方法解决这个问题,写出解决这个问题的主要步骤及估算方法.
答案:
例题经典
例1:9张 例2:略 例3:20000条
考点精练
1.A 2.B 3.B 4.D 5.48 6.![]()
7.12500人 8.25个 18个 29个
9.摸到两个红球
10.解:根据题意,以(m,n)为坐标的点A共有36个,
而只有(1,2),(2,4),(3,6)三个点在函数y=2x图象上,
所以,所求概率是![]() =
=![]() ,即:点A在函数y=2x图象上的概率是
,即:点A在函数y=2x图象上的概率是![]()
11.(1)y=![]() x (2)x=15,y=25
x (2)x=15,y=25
12.(1)利用列表法得出所有可能的结果,如右表:
| 1 | 2 | 3 | 4 | |
| 5 | 5 | 10 | 15 | 20 |
| 6 | 6 | 12 | 18 | 24 |
| 7 | 7 | 14 | 21 | 28 |
| 8 | 8 | 16 | 24 | 32 |
由表格可知,该游戏所有可能的结果共16种,其中两张卡片上的数字之积大于20的有5种,所以甲获胜的概率为P甲=![]()
(2)这个游戏对双方不公平,因为甲获胜的概率P甲=![]() ,
,
乙获胜的概率P乙=![]() ,
,![]() ≠
≠![]() ,所以,游戏对双方是不公平的.
,所以,游戏对双方是不公平的.
13.![]()
14.(1)![]() (2)
(2)![]()
15.(1)0.6 (2)0.6,0.4
(3)黑球有8个,白球12个 (4)略
