第四节 圆的有关计算

【回顾与思考】

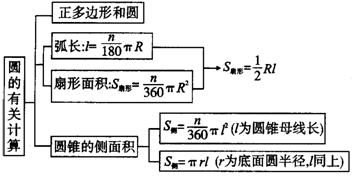
【例题经典】

有关弧长公式的应用

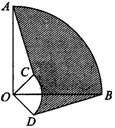
例1  如图，Rt△ABC的斜边AB=35，AC=21，点O在AB边上，OB=20，一个以O为圆心的圆，分别切两直角边边BC、AC于D、E两点，求的长度．

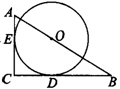
　　【分析】求弧长时，只要分别求出圆心角和半径，特别是求半径时，要综合应用所学知识解题，如此题求半径时，就用到了相似．

有关阴影部分面积的求法

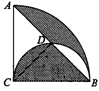
例2　（2006年济宁市）如图，以BC为直径，在半径为2圆心角为90°的扇形内作半圆，交弦AB于点D，连接CD，则阴影部分的面积是（　）

　　A．-1　　　B．-2　　　C．-1　 　D．-2

　　【分析】有关此类不规则图形的面积问题，一般采用“割补法”化为几个已学过的规则图形求解．

求曲面上最短距离

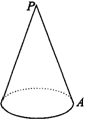
例3　（2006年南充市）如图，底面半径为1，母线长为4的圆锥，一只小蚂蚁若从A点出发，绕侧面一周又回到A点，它爬行的最短路线长是（  ）

　　A．2　　  B．4　　 C．4　　  D．5

　　【分析】在曲面上不好研究最短距离问题，可以通过展开图把曲面问题转化成平面问题，利用“两点之间，线段最短”来解决问题．

【考点精练】

一、基础训练

1．已知扇形的圆心角为120°，半径为2cm，则扇形的弧长是_______cm，扇形的面积是________cm²．

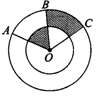
2．如图1，两个同心圆中，大圆的半径OA=4cm，∠AOB=∠BOC=60°，则图中阴影部分的面积是______cm²．

　　　 

　　　　  （1）　　　　　  （2）　　　　　　 （3）　　　　　  （4）

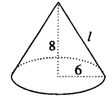
3．如图2，圆锥的底面半径为6cm，高为8cm，那么这个圆锥的侧面积是_______cm²．

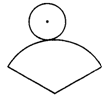
4．如图3，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径为r，扇形的半径为R，扇形的圆心角等于120°，则r与R之间的关系是（ ）

　　A．R=2r　　 B．R=r　　 C．R=3r　　 D．R=4r

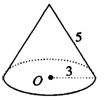
5．如图4，圆锥的底面半径为3cm，母线长为5cm，则它的侧面积是（　）

　　A．60cm²　　 B．45cm²　　 C．30cm²　　 D．15cm²

6．（2006年南通市）已知圆锥侧面展开图的圆心角为90°，则该圆锥的底面半径与母线长的比为（  ）

　　A．1：2　　 B．2：1　　 C．1：4　　 D．4：1

7．（2006年威海市）用半径为30cm，圆心角为120°的扇形围成一个圆锥的侧面，则圆锥的底面半径为（　）

　　A．10cm　　 B．30cm　　 C．45cm　　 D．300cm

8．（2006年江阴市）将直径为64cm的圆形铁皮，做成四个相同圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的高为（　）

　　A．8cm　　 B．8cm　　 C．16cm　　　D．16cm

9．（2006年徐州市）如图5，圆心角都是90°的扇形OAB与扇形OCD叠放在一起，OA=3，OC=1，分别连结AC、BC，则圆中阴影部分的面积为（  ）

A．　　　 B．　　　　 C．2　　　 D．4

　　　　　

　　　　　 （5）　　　　　　　　 （6）　　　　　　　　　　  （7）

二、能力提升：

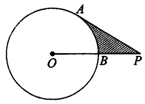
10．如图6，PA切圆O于A，OP交圆O于B，且PB=1，PA=，则阴曩部分的面积S=______．

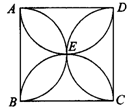
11．如图7，在边长为4cm的正方形ABCD中，分别以各边为直径向正方形内依次作，点E是四段弧的交点．一只蚂蚁由点A出发沿路径顺序不断地爬行，当它行走了2006cm时，停止爬行，此时，蚂蚁所处的位置是点_______．（填A，B，C，D，E之一）

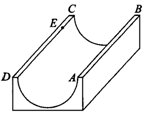
12．如图8，这是一个供滑板爱好者使用的U形池，该U型池可以看作是一个长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是半径为4m的半圆，其边缘AB=CD=20m，点E在CD上，CE=2m，一滑板爱好者从A点滑到E点，则他滑行的最短距离约为______m；（边缘部分的厚度忽略不计，结果保留整数）

　　　　　

　　　　 （8）　　　　　　　　　 （9）　　　　　　　　  （10）

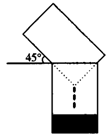
13．（2006年长春市）如图9，将圆桶中的水倒入一个直径为40cm，高为55cm的圆口容器中，圆桶放置的角度与水平线的夹角为45°，若使容器中的水面与圆桶相接触，则容器中水的深度至少应为（  ）

　　A．10cm　　　B．20cm　　　C．30cm　　 D．35cm

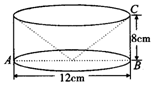
14．（2006年贵阳市）如图10，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB=12cm，高BC=8cm，求这个零件的表面积．（结果保留根号）

15．半径为1的圆的内接正三角形、正四边形、正六边形的边心距分别为多少？它们的长不能构成三角形吗？若能将构成什么形状的三角形？若不能说明理由．

三、应用与探究：

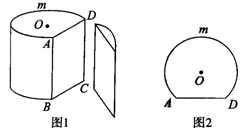
16．（2006年烟台市）如图，O是圆柱形木块底面的圆心，过底面的一条弦AD，沿母线AB剖开，得剖面矩形ABCD，AD=24cm，AB=25cm，若的长为底面周长的，如图所示：

　　（1）求⊙O的半径；

　　（2）求这个圆柱形木块的表面积．（结果可保留根号）

答案：

例题经典　

例1：6　例2：A　例3：B

考点精练　

1．，　2．　3．60　4．C  5．C　6．C　7．A  8．A　9．C　

10．　11．D  12．22　13．D　

14．解：这个零件的底面积=×（）²=36cm²  

这个零件的外侧面积=12×8=96cm²　圆锥母线长OC==10cm　

这个零件的内侧面积=×12×10=60cm²，

∴这个零件的表面积为：36+96+60=192cm²　

15．分别为，，，能构成直角三角形　

16．解：（1）连结OA、OD，作OE⊥AD于E，

易知∠AOD=120°，AE=12cm，可得AO=r==8cm　

（2）圆柱表面积=2S_圆+S_圆=（384+400）cm²