高中入学综合调研数学试卷

一、填空题(共48分)

1．计算：_______________．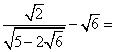

2．设x为正整数，且满足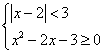，则x=_________________．

3．在△ABC中，P是线段AB上的点、Q是线段AC延长线上的点，且AP：PB=2：1

　AQ：QC=4：1，PQ和BC交于M，则BM：MC= ______________．

4．，，一次函数图象上

两点为P₁(x_l，y₁)，P₂ (x₂，y₂)且，则________．

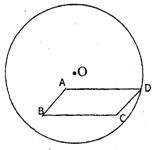
5．如图：圆O内挖去一个平行四边形ABCD，现将图形用一直线切开，使其面积被平分。(将作图痕迹保留，用字母表示该直线为PQ)

6．设a、b满足，则的最大值为__________．

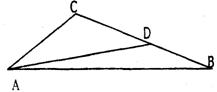7．在△ABC中，AC=CD且∠CAB=∠ABC=30°，

则∠BAD=__________．

8．设，则中

最大的数为________．

9．某商店有A种练习本出售，如买一本为0．30元，买一打(12本)为3．00元，买10打以上每打为2．70元，某年级有227人，每人需要一本，则最少需付__________元．

10．设是方程的两根，△ABC的三边分别为，则△ABC的形状是______________三角形．

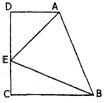11．如图：直角梯形ABCD中，AD∥CB，∠DCB=90°，

AD＜CB，E为CD上一点，∠ABE=45°，AE=10，

BC=CD=12，则CE=_______________．

12．设x、y满足，则__________．

二、解答题(共52分)

………（2）

…（1）

13．(8分)解方程组：

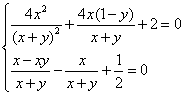
14．(10分)在某一次自行车1000米场地追逐赛中(一圈为1000米)，甲运动员的战术为：

第一分钟的速度为1000米／分，以后每分钟递增200米，到第5分钟时由于体力下降，则以每分钟递减200米，直至最低速度为600米／分，乙运动员的战术为1200米／分均速前进。比赛规则规定：两人同时、同地、同向出发，追上一圈者获胜。

问：(1)甲运动员在最高时速时，能否追上乙．

(2)比赛结束时，比赛进行了多长时间。　　

15．(10分)方程有且只有一个根。求的取

值范围．

16．(10分)在△ABC中，H为垂心，M为BC上的中点，

AD为BC上的高，且AD=BC(AC＞AB)．

求证：HD+HM=MC．

17．(14分)已知一次函数，二次函数和

的图象分别为、E₁、E₂，交E₁于B、C两点，且满足下列条件：

I)b为整数．

II)B()，C()．

Ⅲ)两个二次函数的最小值差为l．

　 (1)如与E₂交于A、D两点，求值．

　 (2)问是否存在一点P，从P出发作一射线分别交E₁、E₂于P₁，P₂，

使得P P₁：P P₂为常数，并简述你的理由。