高中提前批招生数学模拟卷(含答案)

一、选择题(共8题，每题５分，共40分)：

1．国家质检总局出台了国内销售的纤维制品甲醛含量标准, 从2003年1月1 日起正式实施.该标准规定:针织内衣. 床上用品等直接接触皮肤的制品,甲醛含量应在百万分之七十五以下. 百万分之七十五用科学记数法表示应写成．．．．．．．．．．．．．．．．．．．．．．．．．(　　 )
A．75×10^-7；　　 B．75×10^-6；　　 C．7.5×10^-6；　　 D．7.5×10^-5

2．如图：是一个正方体的平面展开图，当把它拆成一个正方体，

与空白面相对的字应该是．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（　　）

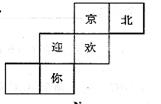　A．北　　 　　 B．京　　　 　　C．欢　　　　　　 D．迎

3．若是二次函数　　　　　　　的图象上的两点,且，则当时，的值为．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（ 　　）

A．0　　　 　　 B．　　　　　 C．　　  　　 D．

4．如图,有三根长度相同横截面为正方形的直条形木块、、，若将它们靠紧放

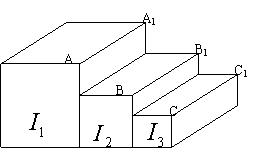置在水平地面上时，且A、B、C恰在一直线上，木块、、的体积分别为、、，则下列结论中正确的是……………（ 　　）

A． 　　 B．

C． 　D．

５．红星学校准备开办一些学生课外活动的兴趣　　　　班，结果反应热烈。各种班的计划招生人数和报名人数，列前三位的如下表所示

班	计算机	奥数	英语口语
计划人数	100	90	60

班	计算机	英语口语	音乐艺术
报名人数	280	250	200

若计划招生人数和报名人数的比值越大，表示学校开设该兴趣班相对学生需要的满足程度就越高，那么根据以上数据，满足程度最高的兴趣班是．．．．．．．．．．．（　　 ）

A．计算机班；　　　　  B．奥数班； 　 

C．英语口语班；　　　  D．音乐艺术班

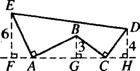6．如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（ 　　）

A．50　　　　　B．62　　　　 C．65 　　　　D．68

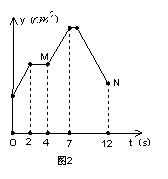7．已知：如图1，点G是BC的中点，点H在AF上，动点P以每秒2的速度沿图1的边线运动，运动路径为：，相应的△ABP的面积关于运动时间的函数图像如图2，若，则下列结论中正确的个数有．．．．．．．．．．．．．．．．．．．．．（　　 ）

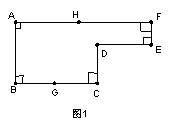
 (1)图1中的BC长是8　　(2)图2中的M点表示第4秒时的值为24

(3)图1中的CD长是4　　(4)图2中的N点表示第12秒时的值为18

A．1个　　　 B．2个　　　 C．3个　　　  D．4个

8．在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，AB=AE，AC=AD. 那么在下列四个结论中：（1） AC⊥BD；（2）BC=DE； （3）∠DBC=∠DAB；（4） △ABE是正三角形，正确的是．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(　　　)
A．（1）和（2）；　 　B．（2）和（3）；　 　 C．（3）和（4）；　　　 D．（1）和（4）

二、填空题(共8题，每题5分，共40分)

9．一元二次方程有根的k的取值范围是________________.

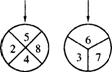10．如图，两个标有数字的轮子可以分别绕轮子的中心旋转，旋转停止时，每个轮子上方的箭头各指着轮子上的一个数字，若左图轮子上方的箭头指着的数字为a，右图轮子上方的箭头指着的数字为b，数对（a，b）所有可能的个数为n，其中a+b恰为偶数的不同数对的参数为m，则m/n等于_____________.

11．如图，圆柱形开口杯底部固定在长方体水池底，向水池匀速注入水（倒在杯外），水池中水面高度是h，注水时间为t，则h与t之间的关系大致为下图中的 　　　　　（填标号）.

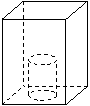
⑴　　　　　　 ⑵　　　　　　  ⑶　　　　　  ⑷

　　　　　　　　 　　　　　　　　　　　　　　

12．在平面直角坐标系中，点A的坐标为（0，4），点B的坐标为（-1，0），以线段AB上一点P为圆心作圆与OA，OB均相切，则点P的坐标 　　　　　　　.

13．等腰△ABC的底边BC=8cm，腰长AB=5cm，一动点P在底边上从点B开始向点C以0.25cm/秒的速度运动, 当点P运动到PA与腰垂直的位置时，点P运动的时间应为　　秒.

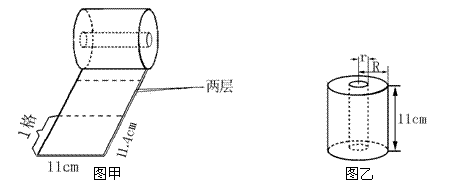
14．从卫生纸的包装纸上得到以下资料：两层300格，每格11.4cm×11cm，如图甲。用尺

量出整卷卫生纸的半径（）与纸筒内芯的半径（），分别为5.8cm和2.3cm，如图乙。那么该两层卫生纸的厚度为　　　　　  cm.（π取3.14，结果精确到0.001cm）

 

15．定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n＋5；②当n为偶数时，结果为（其中k是使为奇数的正整数），并且运算重复进行．

例如，取n＝26，则：

若n＝449，则第449次“F运算”的结果是　　　　 ．

16．把三根长为1cm的火柴杆和三根长为3cm的火柴杆摆放成如右图所示的圆周上，构成一个六边形，那么此六边形的面积是由三根长为1cm的火柴杆所构成的等边三角形面积的　　　　　　　倍．

三、解答题(共5题，10分+14分+14分+16分+16分=70分)

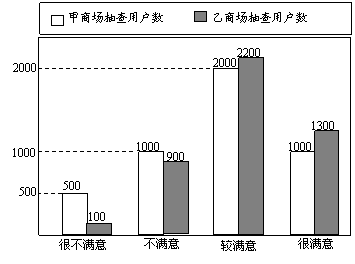17．在“3.15”消费者权益日的活动中，对甲、乙两家商场售后服务的满意度进行了抽查. 如图反映了被抽查用户对两家商场售后服务的满意程度（以下称：用户满意度），分为很不满意、不满意、较满意、很满意四个等级，并依次记为1分、2分、3分、4分.

（1）请问：甲商场的用户满意

度分数的众数为　　　 ;

乙商场的用户满意度分数的众数为　　  .

（2）分别求出甲、乙两商场的用户满意度分数的平均值（计算结果精确到0.01）.

（3）请你根据所学的统计知识,判断哪家商场的用户满意度较高,并简要说明理由.

18．池塘中竖着一块碑，在高于水面1米的地方观测，测得碑顶的仰角为，测得碑顶在水中倒影的俯角为（研究问题时可把碑顶及其在水中的倒影所在的直线与水平线垂直），求水面到碑顶的高度（精确到0.01米，）

19．A地产汽油，B地需要汽油，汽车自A地运汽油往B地，往返所需的汽油正好等于满载汽油的吨数，故无法直接自A地运往B地．因此，需在中途设一油库为中间站C，自A往返于A、C间的汽车将油从A地运送至C地，然后再由往返于C、B间的汽车将油从C地运至B地．设A、B两地的路程为s，B地收到的汽油吨数与A地运出汽油的吨数之比为运油率k．
（1）当AC＝s时，求运油率k的值．
（2）当AC为何值时，运油率最大？并求出此时的运油率k．　

20．在等腰梯形ABCD中，AB=DC=5，AD=4，BC=10. 点E在下底边BC上，点F在腰AB上.

（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF的面积；

（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此时BE的长；若不存在，请说明理由；

（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分？若存在，求出此时BE的长；若不存在，请说明理由.

21.某校部分住校生，放学后到学校锅炉房打水，每人接水2升，他们先同时打开两个放水笼头，后来因故障关闭一个放水笼头．假设前后两人接水间隔时间忽略不计，且不发生泼洒，锅炉内的余水量y(升)与接水时间x(分)的函数图象如图．

　　请结合图象，回答下列问题：

　　(1)根据图中信息，请你写出一个结论；

　　(2)问前15位同学接水结束共需要几分钟?

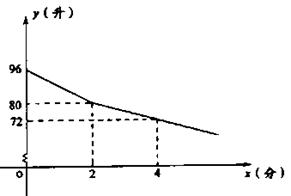　　(3)小敏说：“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟．”你说可能吗?请说明理由．

 参考答案

一、选择题

1．Ｄ　　２．Ｃ　　３．Ｂ　　４．Ｄ　　５．Ｂ　　６．Ａ　　７．Ｄ　　８．Ｂ

二、填空题

9．　　　10.　5/12　　　 11.(2)　　　　12.(-4/5，4/5)　

13．7或 25　　　　　　 14 .0.026　　　  15.8　　　　 16.22

17．解：（1）3；3-----------------------------------------------------------------------------------（２分）

（2）甲商场抽查用户数为：500＋1000＋2000＋1000＝4500（户）

　　 乙商场抽查用户数为：100＋900＋2200＋1300＝4500（户）　　　------------（３分）

所以甲商场满意度分数的平均值＝ ≈2.78（分）

　-----------（５分）

　　乙商场满意度分数的平均值＝ ≈3.04（分）

　答：甲、乙两商场用户满意度分数的平均值分别为2.78分、3.04分.-------------（7分）

（3）因为乙商场用户满意度分数的平均值较高(或较满意和很满意的人数较多)，

所以乙商场的用户满意度较高．----------------------------------------------------------------（10分）

18.解：如图，DE表示水面，A表示观测点，

B为碑顶，在水中的倒影，由题意：

　　

　　

　　设,则

　　在Rt△ABC中，　1

　　在Rt△AC中，　2

　　由1、2得

　　

　　米

　　答：水面到碑顶的高度4.41米.

19．解：（1）设满车载油吨，则汽车A地灌油到C地，可输入油库吨，

故A地到C地的运油率为　　……………………（3分）

同理：C地到B地的运油率为 ……………………（4分）

∴　　　　 　　　……………………（6分）

（2）设AC=，则A地到C地的运油率为　 ………………（8分）

C地到B地的运油率为　　　 ……………………（10分）

∴A地到B地的运油率　 ………（12分）

故当时，运油率最大为　　 ……………………（14分）

　20．（1）由已知条件得：

梯形周长为12，高4，面积为28。

过点F作FG⊥BC于G

过点A作AK⊥BC于K

则可得：FG=×4

∴S△BEF=BE·FG=－x²+x（7≤x≤10）　　　

（2）存在　　　　　　　　　　　　　　　　　　　　　　

由（1）得：－x²+x=14

得x₁=7　　　 x₂=5（不合舍去）

∴存在线段EF将等腰梯形ABCD的周长与面积同时平分，此时BE=7

（3）不存在　　　　　　　　　　　　　　　　　　　　　

假设存在，显然是：S_△BEF∶S_AFECD=1∶2，(BE+BF)∶(AF+AD+DC)=1∶2

则有－x²+x=

整理得：3x²－24x+70=0

△=576－840<0

∴不存在这样的实数x。

即不存在线段EF将等腰梯形ABCD的周长和面积。

同时分成1∶2的两部分　　　　　　　　　　　　

21．解：（1）锅炉内原有水96升；接水2分钟后，锅炉内的余水量为80升；接水4分钟后，锅炉内的余水量为72升；2分钟前的水流量为每分钟8升等．

　　（2）当0≤x≤2时，

　　设函数解析式为y=k₁x+b₁，

　　把x=0，y=96和x=2，y=80代入得：

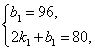　　 解得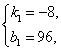

　　∴y=-8x+96（0≤x≤2）．

　　当x>2时，

　　设函数解析式为y=k₂x+b₂，

　　把x=2，y=80和x=4，y=72代入得：

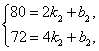　　解得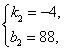

　　∴y=-4x+88（x>2）．

　　因为前15位同学接完水时余水量为96-15×2=66（升），

　　所以　66=-4x+88，

　x=5.5．

　　答：前15位同学接完水需5.5分钟．

　　（3）①若小敏他们是一开始接水的，则接水时间为8×2÷8=2（分），

　　即8位同学接完水，只需要2分钟，与接水时间恰好3分钟不符．

　　②若小敏他们是在若干位同学接完水后开始接水的，设8位同学从t分钟开始接水．当0<t≤2时，

　　则 8（2-t）+4[3-（2-t）]=8×2，

　　16-8t+4+4t=16，

　　∴t=1（分）．

　　∴（2-t）+[3-（2-t）]=3（分），符合．

　　当t>2时，

　　则 8×2÷4=4（分）．

　　即8位同学接完水，需4分钟，与接水时间恰好3分钟不符．

　　所以小敏说法是可能的，即从1分钟开始8位同学连续接完水恰好用了3分钟．