高中提前招生数学试卷

1．已知关于x的方程mx+2=2（m—x）的解满足x－－1=0，则m的值是　　　（　）

A．10或　　B．10或－　　c.－10或　　D．－10或

2．设直角三角形的三边长分别为a、b、c，若c－b=b－a>0，则　　  （　　）

A．1/2　  B．1/3　　C．1/4　　D．1/5

3．某工厂第二季度的产值比第一季度的产值增长了x％，第三季度的产值又比第二季度的产值增长了x％，则第三季度的产值比第一季度的产值增长了　（　　）

A．2x％　　 B． 1+2x％　　C．（1+x％）x％　 D．（2+x％）x％

4．甲从一个鱼摊上买了三条鱼，平均每条a元，又从另—个鱼摊上买了两条鱼，平均每条b元，后来他又以每条元的价格把鱼全部卖给了乙，结果发现赔了钱，原因是　　　（　）

A．a>b 　　　 B．a<b 　　　C．a=b　　　　 D．与a和b的大小无关　　

5．若D是△ABC的边AB上的一点，∠ADC=∠BCA，AC=6，DB=5，△ABC的面积是S，则△BCD的面积是　　（　）

A．　B． 　C．　 D．

6．如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（　）

A．50　　B．62　　 C．65 　　D．68

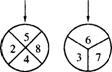7．如图，两个标有数字的轮子可以分别绕轮子的中心旋转，旋转停止时，每个轮子上方的箭头各指着轮子上的一个数字，若左图轮子上方的箭头指着的数字为a，右图轮子上方的箭头指着的数字为b，数对（a，b）所有可能的个数为n，其中a+b恰为偶数的不同数对的参数为m，则m/n等于　　（　）

A．　　 B． 　　C．　　D．

8．如图，甲、乙两动点分别从正方形ABCD的顶点，A、C同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行，若乙的速度是甲的速度的4倍，则它们第2000次相遇在边　　（　）

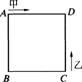
A．AB上　　B．BC上 　　C．CD上　　　 D．DA上

9．已知与和等于，则a=　　　　，b=　　　　

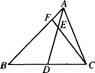10．如图，AD是△ABC的中线，E是AD上的一点，且AE=AD，CE交AB于点F。若AF=1．2cm，则AB=　　　　cm。

11．在梯形ABCD中，AB∥CD，AC．BD相交于点O，若AC=5，BD=12，中位线长为，△AOB的面积为S₁，△COD的面积为S₂，则=　　　　

12．已知矩形A的边长分别为a和b，如果总有另一矩形B，使得矩形B与矩形A的周长之比与面积之比都等于k，则k的最小值为　　　　。

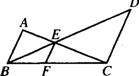
13．如图，AB∥EF∥CD，已知　AC+BD=240，BC=100，EC+ED=192，求CF。

14．已知x、y均为实数，且满足xy+x+y=17，x²y+xy²=66，求x⁴+x³y+x²y²+xy³+y⁴的值。

15．将数字1，2，3，4，5，6，7，8分别填写到八边形ABCDEFGH的8个顶点上，并且以S₁，S₂，…，S₈分别表示（A，B，C），（B，C，D），…，（H，A，B）8组相邻的三个顶点上的数字之和。

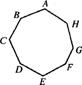（1）试给出一个填法，使得S₁，S₂，…，S₈都大于或等于12；

（2）请证明任何填法均不可能使得S₁，S₂，…，S₈都大于或等于13。

高中提前招生数学试卷

参考答案

1．A

2．C　

3．D　

4．A　

5．C　

6．A　

7．C　

8．A

9．2；2

10．6

11．

12．

13．因为AB∥EF∥CD，所以由平行线分线段成比例定理，得：

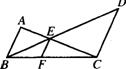
①，②

①+②，得③

由③中取适合已知条件的比例式，得

将已知条件代入比例式中，得，

所以，CF=80

14．由已知xy+x+y=17，xy（x+y）=66，

所以xy和x+y是方程t²－17t+66=0①的两个实数根，

解方程①，得t₁=6，t₂=11，

即xy=6，x+y=11或xy=11，x+y=6，

当xy=6，x+y=11时，x、y是方程u²－11u+6=0②的两个根，

因为Δ₁=（－11）²－4·6=121－24>0，所以方程②有实数根，

这时，x²+y²=（x+y）²－2x y=11²－2·6=121－12=109

当xy=11，x+y=6时，x、y是方程v²－6v+11=0③的两个根。

因为Δ₂=（－6）²－4·11=36－44<0，所以方程③没有实数根，

所以x⁴+x³y+x²y²+xy³+y⁴的值为12499。

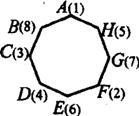
15．（1）不难验证，如图所示填法满足S₁，S₂，…S₈都大于或等于12。

（2）显然，每个顶点出现在全部8组3个相邻顶点组的3个组中，

所以有S₁+S₂+…+S₈=（1+2+3+…+8）·3=108

如果每组三数之和都大于或等于13，因13·8=104，所以至多有108－104＝4个组的三数之和大于13。

由此我们可得如下结论：

（1）相邻两组三数之和一定不相等。设前一组为（i，j，k），后一组为（j，k，l）。若有i+j+k=j+k+l，则l=i，这不符合填写要求；

（2）每组三数之和都小于或等于14。因若有一组三数之和大于或等于15，则至多还有另外两个组，其三数之和大于13，余下5个组三数之和等于13，必有相邻的两组相等，这和上述结论（1）不符。因此，相邻两组三数之和必然为13或14。不妨假定1填在B点上，A点所填为i，C点所填为j。

（I）若S₁=i+1+j=13，

则S₂=1+j+l=14，S₃=j+l+k=13，因j>1，这是不可能的。

（II）若S₁=i+1+j=14，

则S₂=1+j+（i－1）=13，S₃=j+（i－1）+2=14，S₄=（i－1）+2+（j－1）=13，这时S₅=14，只能是S₅=2+（j－1）+i，i重复出现。

所以不可能有使得每组三数之和均大于或等于13的填法。