高中提前招生选拔考试数学试卷2
注意事项： 本卷全卷满分为120分,考试时间为100分钟.
一、 填空题（本大题共有7小题，每题5分，共35分）．
1．同时抛掷两枚正方体骰子，所得点数之和为7的概率是 ．
2．设a＞b＞0, a2+b2=4ab，则的值等于 .
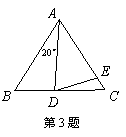
3．如图，在△ABC中，AB=AC，∠BAD=20°，且AE=AD，则∠CDE＝ ．
4．已知实数x、y满足x2－2x+4y＝5，则x+2y的最大值为 ．
5．将正偶数按下表排列：
第1列 第2列 第3列 第4列
第1行 2
第2行 4 6
第3行 8 10 12
第1行 2
第2行 4 6
第3行 8 10 12
第4行 14 16 18 20
……
根据上面的规律，则2006所在行、列分别是 .
6．某学生为了描点作出函数y＝ax2＋bx ＋c（a≠0）的图象，取自变量的7个值，x1＜x2＜……＜x7，且x2－x1＝x3－x2＝……＝x7－x6，分别算出对应的y值，列表如下：
| x | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| y | 51 | 107 | 185 | 285 | 407 | 549 | 717 |
但由于粗心算错了其中一个y值，请指出算错的是___________．（从上述数据中选一个填入）
7．已知四边形ABCD中,AD+DB+BC=16,则四边形ABCD的面积的最大值为 .
二、选择题（本大题共9小题，每小题5分，共45分．在每题所给出的四个选项中，只有一个是符合题意的，请把正确选项前的字母代号填在题后的括号内）
8．方程
的所有整数解的个数是（ ）
A．2个 B．3个 C．4个 D．5个
9. 方程
的解的情况是（ ）
A．仅有一正根 B．仅有一负根 C．有一正根一负根 D．无实根
10．甲、乙、丙、丁四名运动员参加4×100米接力赛，甲必须为第一接力棒或第四接力棒的运动员，那么这四名运动员在比赛过程中的接棒顺序有 ( )
A．3种 B．4种 C．6种 D．12种
11． 如图，圆柱形开口杯底部固定在长方体水池底，向水池匀速注入水（倒在杯外），水池中水面高度是h，注水时间为t，则h与t之间的关系大致为下图中的 （ ）
 |
A． B． C． D．
12．关于x的不等式组只有4个整数解，则a的取值范围是（ ）
A．－5≤a≤－ B．－5≤a＜－ C．－5＜a≤－ D．－5＜a＜－
13． 在3×3方格上做填字游戏，要求每行每列及对角线上三个
方格中的数字和都等于S，又填在图中三格中的数字如图，若要
能填成，则（ ）
A. S=24 B. S=30 C. S=31 D. S=39
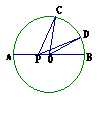
14．如图，已知⊙O的半径是R，C、D是直径AB同侧圆周上的两点，弧AC的度数为960，弧BD的度数为360，动点P在AB上，则PC+PD的最小值为（ ）
A．2R B．
C．
D．R
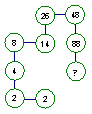
15．观察图形，寻找规律，在“？”填上数字
A．128 B．136 C．162 D．188
16． 一个三角形的边长分别为a,a,b，另一个三角形的边长分别为b,b,a，其中a>b，若两个三角形的最小内角相等，则
的值等于（ ）
A．
B．
C．
D．
三、解答题（本大题共3小题，满分40分，第17题10分，第18、19题15分，共40分）．
17．
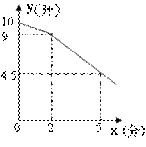
18．课间休息时，同学们到饮水机旁依次每人接水0.25升，他们先打开了一个饮水管，后来又打开了第二个饮水管．假设接水的过程中每根饮水管出水的速度是匀速的，在不关闭饮水管的情况下，饮水机水桶内的存水量
的函数关系图像如图所示．请结合图像回答下列问题：
⑴ 存水量的函数关系式；
⑵ 如果接水的同学有28名，那么他们都接完水需要几分钟？
⑶ 如果有若干名同学按上述方法接水，他们接水所用时间要比只开第一个饮水管接水的时间少用2分钟，那么有多少名学生接完水？
19．已知抛物线y＝ax2＋bx＋c经过点（1，2）．
（1）若a=1，抛物线顶点为A，它与x轴交于两点B、C，且△ABC为等边三角形，求b的值．
（2）若abc=4，且a≥b≥c，求a＋b＋c的最小值.