钱库学区2006年中考数学模拟试卷

  温馨提示： 1、试卷满分150分，答卷时间120分钟；

　 　　　　　  2、允许使用科学计算器。

一选择题（本题共12小题，共48分，每小题只要一个选项是正确的，不选、多选、错选均不得分）

１．下列实数是无理数的是（　　）

（A） 　　（B）3.14　　( C )　　 ( D)　-1

2． 反比例函数的图象经过点（　　　）

（A）（2，3）；　　　　　　 　　　　　　　　　　 （B）（1，6）；

（C）（9，）；　　　　　　　　　　　　　（D）（-2，-3）．

　3．　十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，

黄灯亮5秒.当你抬头看信号灯时，是黄灯的概率是 （　 ）

（A）　　　　  (B) 　　　

（第3题）

(C) 　　　　　(D)  

4． 观察我们学过的大写英文字母，既是轴对称又是中心对称图形的是（　）

（A）　W  （B） X　 （C）Y　（D）Z

5．下列各式计算结果正确的是（　　　 ）

(A) a＋a＝a²　　　　  (B) (3a)²＝6a²　　

(C) (a-1)²＝a²-1　　　(D) a ·a＝a²

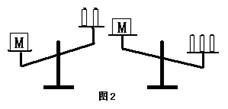
6．如图2，天平右盘中的每个砝码的质量为1g，则物体M的质量m(g)的取值范围，在数轴上可表示为（　　 ）

7． 把抛物线y=x²向左平移3个单位后，得到新的抛物线是（　 ）

(A) y=(x-3)²　　( B) y=(x+3)²　　 (C) y=x²-3　　( D )y=x²+3

8. 如图.DE切⊙O于A，AC是弦，连OA,OC,

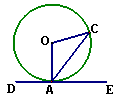
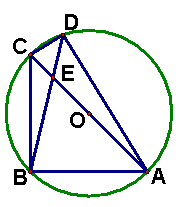
如果∠EAC=55º那么∠AOC=(　　 )

（A） 55º　 (B) 100º　　 (C) 110 º　 (D)120º

	第8题

9． 已知圆锥的高是3，底面半径是4，则这个圆锥的侧面积是（　 ）

（A）12π　 （B）15π　  （C）20 π　 （D）24π

10　若两圆的半径分别为方程x²-6x+5=0的两根，圆心距为3，则两圆的位置关系是（　 ）

（A）内含　 （B）相交　（C）外切　（D）相离

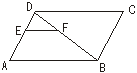
11.如图，在平行四边形ABCD中，EF∥AB,DE:EA=2:3,

EF=4则CD的长为 (　 )

（A） 8　 （B）10　　 （C）16　　（D）12

12．已知D、E分别为△ABC中AB、AC边上的点，直线DE将△ABC的面积分成两部分，其中一部分为x，另一部分为y．当△ABC的面积不变时，则y和x的函数图象为(　 )

							(D)
			(B)
	(A)
					(C)

二 填空题（本题6道题，每小题5分，共30分）

13.计算²=______________

14．某单位全体职工中, 月工资在3000元到4000元的人数为120, 频率是0.3, 那么这个单位的职工总人数是______________.

15．写出一个两根互为倒数的一元二次方程______________.

第16题

16．如图，直线PA切圆O于A点，直线PB交圆O于

C、B，已知PB=BC=5，则PA的长为______________.

17． 如图：已知AB是⊙O的直径，弦CD交AB与E，

AC=AO则 tan∠D=　　

	第17题

18．　小纪念册每本5元，大纪念册每本7元，小明买这两种纪念册共花了142元，则两种纪念册最少共买 　　　　 本

19　　　  (本题满分8分)

将下面的代数式尽可能化简，在选择一个你喜欢的数（要合适哦！）代入求值：　

　　3a-(2a+1)+

20．(本题满分8分)

解方程=-x

21．(本题满分10分)

阅读下题及证明过程：已知：如图，D是△ABC中BC边上的一点，E是AD上的一点，EB=EC,∠ABE=∠ACE求证：∠BAE=∠CAE

　 小明的证法如下：在△AEB与△AEC中,EB=EC, ∠ABE=∠ACE,AE=AE

∴△ABE≌△ACE　 …　　　　  第一步

∴∠BAE=∠CAE　　…　　　　  第二步

 你认为小明的证明过程正确吗？若正确，请写出每一步推理的依据；若不正确，请指出错在哪一步，并写出你认为正确的证明过程.

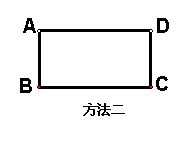
22、(本题满分8分)

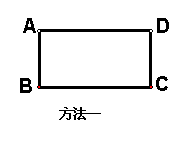
 已知矩形ABCD，AD=2AB，试在图中画出两条线段，把矩形分割成彼此相似的三个三角形，请给出两种不同的方法（工具不限，不要求写画法和证明，但要标出能说明方法的必要记号）。

23．(本题满分10分)

 小李通过对某地区2003年到2005年快餐公司发展情况的调查，制成了该地区快餐公司个数情况的条形图（如图a）和快餐公司盒饭年销量的平均数情况条形图（如图b）利用信息，回答下列问题:

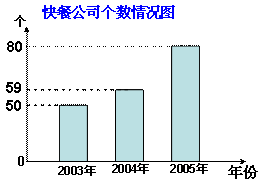
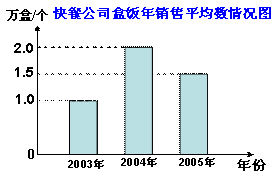
　　　( 图a)　　　　　　　　　　　　　　  ( 图b)

⑴ 请从以上信息所反映的数据中，写出一个精确数______________，

　 一个近似数______________；

⑵ 2004年该地区销售饭盒共______________万盒；

⑶ 该地区销售饭盒最大的年份是　　　 　这一年的销售量是______万盒；

⑷ 求这三年中该地区每年平均销售饭盒多少万盒？

24 (本题满分14分)

.如图, 边长为2的正方形OABC的顶点O为坐标原点，点A在x轴的负半轴上，点C在y轴的正半轴，动点D在线段BC上移动（不与B、Ｃ重合），连接ＯＤ，过点Ｄ作ＤＥ⊥ＯＤ，交边ＡＢ于点Ｅ，连接ＯＥ，设ＣＤ的长为x

①求证:△COD∽△BDE

②当x=时，求直线DE的函数的表达式

③如果梯形COEB的面积为S,问S是否存在最大值？若存在，请求出这个最大值及此时x的值，若不存在，请说明理由？

25．(本题满分14分)

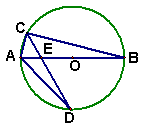
 如图，四边形ABCD内接于⊙O，AC为直径，BD平分∠ADC，

BD与OC相交于E

⑴求证：BC ²＝BE·BD；

⑵若直径AC＝6，BE：ED＝3：1，求OE的值.

⑶点P在圆上，当△PAB的面积分别取何值时，在圆上①只存在一点P；

②存在两点P；③存在三点P；④存在四点P。