中考数学阅读题赏析
近年来,阅读型考题相继出现在一些地区的中考之中。这类题型往往需要先阅读较多的文字,要求考生对文字、符号、图形和式子进行概括、分析,对所提供的材料进行观察、实验、猜想、调整,就其本质进行归纳、加工提炼,然后作出解答。在所提供的材料中,常常出现新的概念和方法,因此,不仅要求考生具备较强的阅读理解能力,而且还要求考生具备一定的归纳推理、抽象思维、文字概括、书面表达、自学和应用等诸方面的能力。
例1 阅读下题和分析过程,并按要求进行证明
已知:四边形ABCD中,AB = DC,AC = BD,AD ≠ BC。
求证:四边形ABCD是等腰梯形。
分析:要证四边形ABCD是等腰梯形,因为AB = DC,所以只要证四边形ABCD是梯形即可;又因为AD ≠ BC,故只需证AD∥BC即可;要证AD∥BC,现有下图所示四种添作辅助线的方法,请任选其中两种图形,对原题进行证明。 (2001青海省)
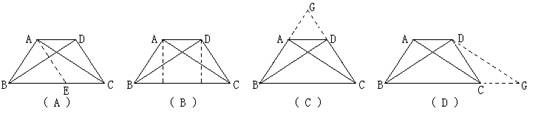
解:(略)
赏析: 所谓梯形,是指一组对边平行而另一组对边不平行的四边形;而等腰梯形是指两腰相等的梯形。该题中的阅读部分从定义出发,明确提出了考生要解决的问题。由于此题给考生提供了解题的思路,考生可根据自身的情况灵活选择方法,降低了难度,使一部分基础较差的考生也可进行尝试。
中考毕竟是选拔性的考查,本题虽然降低了难度,但考查的机能仍未减弱。因为在所给的图形中,只是给考生提供了辅助图形的位置,至于该图形的性质,则需考生根据自身解题的需要来给予界定。比如图(A)中的AE,我们既可以从“在BC边上取点E,使CE = AD,连结AE”来得到,也可以从“过点A作DC的平行线,交BC于点E”来得到,还可以从“以A为圆心、DC为半径画弧,交BC于点E,连结AE”或是以其它方式来获得。考生以怎样的方法来构造该辅助图形,反映了考生的思维。同时,在整个解题过程中,考生是否严格按照“等腰梯形”的定义进行操作、逻辑是否严密等情况,都能较好地反映该考生的基本功。
例2 如图,AB是⊙O的直径,把AB分成几条相等的线段,分别以每条线段为直径画小圆,设AB = ![]() ,那么⊙O的周长
,那么⊙O的周长![]() 。
。
计算:(1)把AB分成两条相等的线段,每个小圆的周长![]()
(2)把AB分成三条相等的线段,每个小圆的周长![]()
(3)把AB分成四条相等的线段,每个小圆的周长![]()
……
(4)把AB分成![]() 条相等的线段,每个小圆的周长
条相等的线段,每个小圆的周长![]()
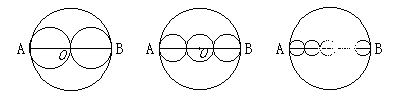
结论:把大圆的直径分成![]() 条相等的线段,分别以每条线段为直径画小圆,那么每个小圆的周长是大圆周长的______倍
条相等的线段,分别以每条线段为直径画小圆,那么每个小圆的周长是大圆周长的______倍
请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系。
(2000浙江省金华、衢州市)
赏析: 本题着重考查学生归纳、推理的能力。
所谓的“三大能力”,历来都为中学数学教学人员所乐道。
归纳思想,是学生在中学阶段的数学学习过程中,需要形成的数学思想之一;发展思维能力和空间观念,是初中数学的教学目的之一。所谓思维能力,“主要是指:会观察、实验、比较、猜想、分析、综合、抽象和概括;会用归纳、演绎和类比进行推理……”[1] ,而这在《数学课程标准》中,同样也有相应的要求。
例3 世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆:它们看上去多么美丽与和谐,这正是因为圆具有轴对称性和中心对称性。
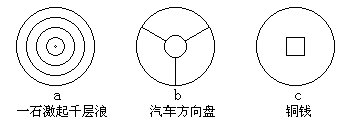
(1)请问:以上三个图形中,是轴对称图形的有________,是中心对称图形的有________(分别用上面三个图的代号a,b,c填空);
(2)请你在下面的两个圆中,按要求分别画出与上面图案不重复的图案(草图,用尺规画或徒手画均可,但要尽可能准确些,美观些)。
a.是轴对称图形,但不是中心对称图形;
b. 既是轴对称图形,又是中心对称图形。(2001浙江省金华、衢州市)
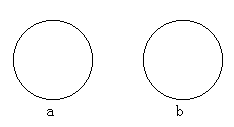
赏析: 《中共中央国务院关于深化教育改革全面推进素质教育的决定》中指出:“实施素质教育,必须把德育、智育、体育、美育等有机地统一在教育活动的各个环节中。学校教育不仅要抓好智育,更要重视德育,还要加强体育、美育、劳动技术教育和社会实践,使诸方面教育相互渗透、协调发展,促进学生的全面发展和健康成长。”
在对学生进行知识掌握情况的考查的同时,唤起学生对美的追求。同时,由于这是一道开放题,更给学生提供了一个创造美好事物的自由畅想空间。
融美育于数学考试之中,此题不可多得。
例4 如图1,在平面上,给定了半径为r的⊙O,对于任意点P,在射线OP上取一点![]() ,使得
,使得![]() ,这种把点P变为
,这种把点P变为![]() 的变换叫做反演变换,点P与点
的变换叫做反演变换,点P与点![]() 叫做互为反演点。
叫做互为反演点。
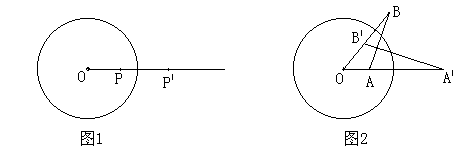
(1)如图2,⊙O内外各有一点A和B,它们的反演点分别为![]() 和
和![]() ,
,
求证:∠![]() =∠B;
=∠B;
(2)如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形。
①选择:如果不经过点O的直线![]() 与⊙O相交,那么它关于⊙O的反演图形是
与⊙O相交,那么它关于⊙O的反演图形是
(A)一个圆 (B)一条直线 (C)一条线段 (D)两条射线
②填空:如果直线![]() 与⊙O相切,那么它关于⊙O的反演图形是________,该图形与⊙O的位置关系是_________________。(2001江苏省南京市)
与⊙O相切,那么它关于⊙O的反演图形是________,该图形与⊙O的位置关系是_________________。(2001江苏省南京市)
解题思路:(1)略
(2)①考生如果能够运用分类思想,则此题不难解也:把直线![]() 上的点分成三类:圆外的点、圆内的点和圆上的点。如果直线
上的点分成三类:圆外的点、圆内的点和圆上的点。如果直线![]() 上的点P在圆外,根据定义,可以推知其反演点P′在圆内;如果点P在圆上,那么其反演点P′还是它自己;如果点P在圆内,那么P′当然在圆外,但是因为直线
上的点P在圆外,根据定义,可以推知其反演点P′在圆内;如果点P在圆上,那么其反演点P′还是它自己;如果点P在圆内,那么P′当然在圆外,但是因为直线![]() 不经过圆心O,所以最大的OP′也是有限的(设圆心O到直线
不经过圆心O,所以最大的OP′也是有限的(设圆心O到直线![]() 的距离是d,则d >
0,有OP′≤
的距离是d,则d >
0,有OP′≤![]() ),这样,直线
),这样,直线![]() 的反演图形就不可能是无限延伸的直线和射线,那么接下来只要把“线段”给排除掉就行了。
的反演图形就不可能是无限延伸的直线和射线,那么接下来只要把“线段”给排除掉就行了。
②一旦解决了①,那么就不难猜测还是圆,虽说是填空题,但能够猜测到是“圆”的考生应该不难在草稿纸上得以证实。
赏析: “将来的文盲,已经不是没有知识的人,而是那些不懂得怎样学习的人。”
当今的社会是一个多变的社会,是一个发展的社会,是一个经济的增长以知识的增长为主要依赖的知识经济社会,是一个知识爆炸的社会。作为一个劳动者来说,他一生所需要的知识,不可能在学校完全学到,加之新知识在不断地出现,这就要求我们的学习者除了学习必要的基础知识、基本技能之外,更主要的是要学会今后进一步学习的能力,简言之,要学会学习。
面对(绝大多数学生)以前从未接触过的新知识,能否迅速学习接受、并进而运用于解决问题?这对学生的收集处理信息的能力、获取新知识的能力、分析和解决问题的能力等能力是一个挑战。
例5 阅读下面材料:
在计算 3+5+7+9+11+13+15+17+19+21 时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值。具有这种规律的一列数,除了直接相加外,我们还可以用公式![]() 来计算它们的和(公式中的n表示数的个数,
来计算它们的和(公式中的n表示数的个数,![]() 表示第一个数的值,d表示这个相差的定值)。
表示第一个数的值,d表示这个相差的定值)。
那么3+5+7+9+11+13+15+17+19+21 = ![]() 。
。
用上面的知识解决下列问题:
为保护长江,减少水土流失,我市某县决定对原有的坡荒地进行退耕还林。从1995年起在坡荒地上植树造林,以后每年又以比上一年多植相同面积的树木改造坡荒地。由于每年因自然灾害、树木成活率、人为因素等的影响,都有相同数量的新坡荒地产生,下表为1995、1996、1997三年的坡荒地面积和植树的面积的统计数据。假设坡荒地全部都种上树后,不再水土流失形成新的坡荒地,问:到哪一年可以将全县所有的坡荒地全部种上树木。
| 1995年 | 1996年 | 1997年 | |
| 每年植树的面积(亩) | 1000 | 1400 | 1800 |
| 植树后坡荒地的实际面积(亩) | 25200 | 24000 | 22400 |
(2001重庆市)
赏析 等差数列,本是学生在高中阶段才涉及的学习内容。和上题一样,面对新出现的知识内容,能否依据自己已有的知识和以往的经验从容应对?这对考生的学习能力是一个很大的考验。
当然,成功的路不止一条。如果考生能够根据所收集到的信息加以分析,直接列表加以处理,同样也能解决问题,这就要看考生的能力了。
多好啊!到了2004年,所有的坡荒地都已经被绿荫所覆盖,这可是我的家乡呀!
例6 阅读下面的短文,并回答下列问题
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体。
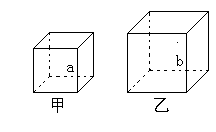 如图,甲、乙是两个不同的立方体,立方体都是相似体,它们的一切对应线段之比都等于相似比(a:b)。
如图,甲、乙是两个不同的立方体,立方体都是相似体,它们的一切对应线段之比都等于相似比(a:b)。
设S甲、S乙 分别表示这两个立方体的表面积,则![]() ,又设V甲、V乙 分别表示这两个立方体的体积,则
,又设V甲、V乙 分别表示这两个立方体的体积,则![]() 。
。
(1)下列几何体中,一定属于相似体的是
(A)两个球体 (B)两个圆锥体 (C)两个圆柱体 (D)两个长方体
(2)请归纳出相似体的三条主要性质:①相似体的一切对应线段(或弧)长度的比等于__________ ;②相似体表面积的比等于________________ ;③相似体体积的比等于________________________ 。
(3)假定在完全正常发育的条件下,不同时期的同一个人的人体是相似体,一个小朋友上幼儿园时身高为1.1米,体重为18千克,到了初三时,身高为1.65米。问他的体重是多少(不考虑不同时期人体平均密度的变化)?(2001江苏省泰州市)
解:(略)
赏析: 将“相似”的概念从平面扩展到空间后,情况会发生什么变化呢?实际上这也不是个什么很复杂问题,因为阅读材料中明确地告诉我们:相似体的“一切对应线段之比都等于相似比”。重要的信息它就明摆在那儿,就看你能否收集到它,并加以分析处理,从而用以解决问题。
“终身学习” 这一概念,其实并不新鲜,联合国教科文组织成人教育局局长保罗·郎格朗于1965年就已提出。1995年,《中华人民共和国教育法》在第十一条中以法律形式明确规定:“推进教育改革,促进各级各类教育协调发展,建立和发展终身教育体系”。1999年,我国在《面向21世纪教育振兴行动计划》中提出,要“构筑知识经济时代人们终身学习的体系”,到2010年,我国将“基本建立起终身学习体系”。而始于2001年的这一轮基础教育课程改革,其主干内容就是为终生学习奠定基础。
我们的学生,需要学会怎样学习,而学习的最重要的基础是阅读。
[1]
