中考中的数学思想方法----分类讨论思想
一、概述:
当我们面对一大堆杂乱的人民币时,我们一般会先分10元,5元,2元,1元,5角,……
等不同面值把人民币整理成一叠叠的,再分别数出各叠钱数,最后把各叠的钱数加起来得出这一堆人民币的总值。这样做,比随意一张张地数的方法要快且准确的多,因为这种方法里渗透了分类讨论的思想。
在数学中,分类思想是根据数学本质属性的相同点和不同点,把数学的研究对象区分为不同种类的一种数学思想,正确应用分类思想,是完整解题的基础。而在中考中,分类讨论思想也贯穿其中,几乎在全国各地的重考试卷中都会有这类试题,命题者经常利用分类讨论题来加大试卷的区分度,很多压轴题也都涉及分类讨论,由此可见分类思想的重要性,下面精选了几道有代表性的试题予以说明。
二、例题导解:
1、(2004年上海市中考题)直角三角形的两条边长分别为6和8,那么这个三角形的外接圆半径等于 .③
 解:①当6、8是直角三角形的两条直角边时,斜边长为10,
解:①当6、8是直角三角形的两条直角边时,斜边长为10,
此时这个三角形的外接圆半径等于![]() ╳ 10 =5
╳ 10 =5
②当6是这个三角形的直角边,8是斜边时,此时这个三角形
的外接圆半径等于![]() ╳ 8=4
╳ 8=4
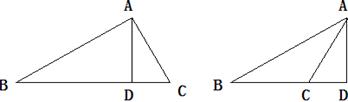 2、(2005年北京市中考题)在△ABC中,∠B=25°,AD是BC边上的高,并且
2、(2005年北京市中考题)在△ABC中,∠B=25°,AD是BC边上的高,并且![]() ,则∠BCA的度数为____________。
,则∠BCA的度数为____________。
解:①如图1,当△ABC是锐角三角形时,
∠BCA=90°-25°=65°
①如图2,当△ABC是钝角三角形时,
∠BCA=90°+25°=115°
图1 图2

3、(2006年济南市中考题)如图1,已知![]() 中,
中,![]() ,
,![]() .过点
.过点![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() 的长;
的长;
(2)以点![]() 为圆心,
为圆心,![]() 为半径作⊙A,试判断
为半径作⊙A,试判断![]() 与⊙A是否相切,并说明理由;
与⊙A是否相切,并说明理由;
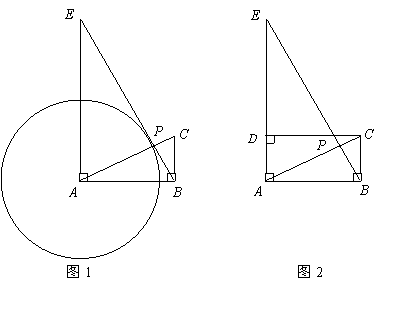 (3)如图2,过点
(3)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() .以点
.以点![]() 为圆心,
为圆心,![]() 为半径作⊙A;以点
为半径作⊙A;以点![]() 为圆心,
为圆心,![]() 为半径作⊙C.若
为半径作⊙C.若![]() 和
和![]() 的大小是可变化的,并且在变化过程中保持⊙A和⊙C相切,且使
的大小是可变化的,并且在变化过程中保持⊙A和⊙C相切,且使![]() 点在⊙A的内部,
点在⊙A的内部,![]() 点在⊙A的外部,求
点在⊙A的外部,求![]() 和
和![]() 的变化范围.
的变化范围.
(1)![]() 在
在![]() 中,
中,![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() .
.
![]() ,
,![]() .
.
(2)![]() 与⊙A相切.
与⊙A相切.
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
![]() 与⊙A相切.
与⊙A相切.
(3)因为![]() ,所以
,所以![]() 的变化范围为
的变化范围为![]() .
.
当⊙A与⊙C外切时,![]() ,所以
,所以![]() 的变化范围为
的变化范围为![]() ;
;
当⊙A与⊙C内切时,![]() ,所以
,所以![]() 的变化范围为
的变化范围为![]() .
.

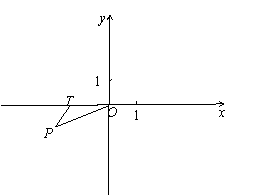 4、(2006年上海市普陀区中考模拟题)直角坐标系中,已知点P(-2,-1),
4、(2006年上海市普陀区中考模拟题)直角坐标系中,已知点P(-2,-1),
点T(t,0)是x轴上的一个动点.
(1)
求点P关于原点的对称点![]() 的坐标;
的坐标;
(2)
当t取何值时,△![]() TO是等腰三角形?
TO是等腰三角形?
解:(1)点P关于原点的对称点![]() 的坐标为(2,1).
的坐标为(2,1).
(2)![]()
![]() .
.
(a)动点T在原点左侧.
当![]() 时,△
时,△![]() 是等腰三角形.
是等腰三角形.
∴点![]() .
.
(b)动点T在原点右侧.
 ①当
①当![]() 时,△
时,△![]() 是等腰三角形.
是等腰三角形.
得:![]() .
.
②
当![]() 时,△
时,△![]() 是等腰三角形.
是等腰三角形.
得:点![]() .
.
③
当![]() 时,△
时,△![]() 是等腰三角形.
是等腰三角形.
得:点![]() .
.
综上所述,
符合条件的t的值为![]() .
.
5、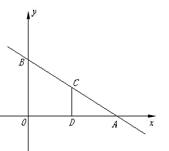 如图,平面直角坐标系中,直线AB与
如图,平面直角坐标系中,直线AB与![]() 轴,
轴,![]() 轴分别交于A(3,0),B(0,
轴分别交于A(3,0),B(0,![]() )两点, ,点C为线段AB上的一动点,过点C作CD⊥
)两点, ,点C为线段AB上的一动点,过点C作CD⊥![]() 轴于点D.
轴于点D.
(1)求直线AB的解析式;
(2)若S梯形OBCD=![]() ,求点C的坐标;
,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的
三角形与△OBA相似.若存在,请求出所有符合条件
的点P的坐标;若不存在,请说明理由.
解:(1)直线AB解析式为:y=![]() x+
x+![]() .
.
(2)方法一:设点C坐标为(x,![]() x+
x+![]() ),那么OD=x,CD=
),那么OD=x,CD=![]() x+
x+![]() .
.
∴![]() =
=![]() =
=![]() .
.
由题意:![]() =
=![]() ,解得
,解得![]() (舍去)
(舍去)
∴ C(2,![]() )
)
方法二:∵ ![]() ,
,![]() =
=![]() ,∴
,∴![]() .
.
由OA=![]() OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD=![]() CD.
CD.
∴ ![]() =
=![]() CD×AD=
CD×AD=![]() =
=![]() .可得CD=
.可得CD=![]() .
.
 ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2,![]() ).
).
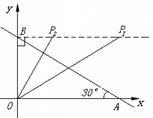
(3)当∠OBP=Rt∠时,如图
①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=![]() OB=3,
OB=3,
∴![]() (3,
(3,![]() ).
).
②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=![]() OB=1.
OB=1.
∴![]() (1,
(1,![]() ).
).
当∠OPB=Rt∠时
③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30°
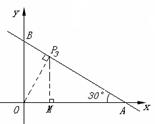 过点P作PM⊥OA于点M.
过点P作PM⊥OA于点M.
方法一: 在Rt△PBO中,BP=![]() OB=
OB=![]() ,OP=
,OP=![]() BP=
BP=![]() .
.
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM=![]() OP=
OP=![]() ;PM=
;PM=![]() OM=
OM=![]() .∴
.∴![]() (
(![]() ,
,![]() ).
).
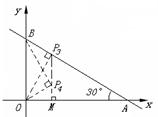 方法二:设P(x ,
方法二:设P(x ,![]() x+
x+![]() ),得OM=x ,PM=
),得OM=x ,PM=![]() x+
x+![]()
由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM==![]() =
=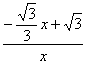 ,tan∠ABO=
,tan∠ABO=![]() =
=![]() .
.
∴![]() x+
x+![]() =
=![]() x,解得x=
x,解得x=![]() .此时,
.此时,![]() (
(![]() ,
,![]() ).
).
④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°.
∴ PM=![]() OM=
OM=![]() .
.
∴ ![]() (
(![]() ,
,![]() )(由对称性也可得到点
)(由对称性也可得到点![]() 的坐标).
的坐标).
当∠OPB=Rt∠时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:
![]() (3,
(3,![]() ),
),![]() (1,
(1,![]() ),
),![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ).
).
