2005年中学复习函数测试题

(全卷完成时间40分钟、满分100分)

一、选择题:（本题共６小题，每小题４分，共24分）

１.点P（a，b）在第二象限，则点Q(a-１，b+1)在(　　 )毛

　（A） 第一象限　　（B） 第二象限　（C） 第三象限　　(D)第四象限

２.下列函数中,自变量的取值范围选取错误的是(　　)

　 (A)中, 取全体实数　　 　 (B)中, 取的实数

　 (C)中, 取的实数　　(D)中, 取的实数

３.当路程Ｓ一定时，速度Ｖ与时间t之间的函数关系是（　　）

　  (A)正比例函数　　　（B）反比例函数 败涂地 （C）一次函数　　（D）二次函数

４.一次函数的图象不经过(　　)

（A）第一象限　 　 (B)第二象限　　 (C)第三象限　　  (D)第四象限

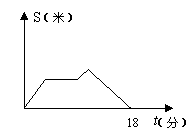５.星期天晚饭后，小红从家里出发去散步，图描述了她散步过程中离家s（米）与散步所用的时间t(分)之间的函数关系．依据图象，下面描述符合小红散步情景的是（　　 ）

(A)从家出发,到了一个公共阅报栏,看了一会报后,

就回家了.

　(B)从家出发,一直散步(没有停留),然后回家了.

(C)从家出发,到了一个公共阅报栏,看了一会报后,

继续向前走了一会,然后回家了.

 (D)从家出发,散了一会步,就找同学去了,18分钟后

才开始返回.

6．直线与曲线的两个交点的坐标是（　　）

（A）（，1），（1，2）　　　　　  （B）（，），（1，2）

（C）（2，），（，）　　　　 （D）（，1），（1，）

二、填空题：（本小题共6个小题，每小题4分，共24分）

７.点A（-3，2）关于y轴对称的点的坐标是　　　　　　　　．

８.如果正比例函数及反比例函数图象都经过点（-2，4），则正比例函数的解析式为　　　　　　　 ．反比例函数的解析式为　　　　　　　　  ．

９.抛物线的顶点坐标是　　　　　　；对称轴是　　　　　．

10．二次函数与轴有　　　　　交点．交点坐标是　　　　　 ．

11．已知是整数，且一次函数的图象不过第二象限，则m=　　　

12．直线y =与两坐标轴围成的三角形面积是　　　　　　　   

三、(本小题共４小题，13、14题每题12分,15、16题每题14分，共52分)

13.已知四点Ａ(１，２），Ｂ(３，０），Ｃ(－２，20），Ｄ(－１，12）。试问：是否存在一个二次函数,使它的图象同时经过这四个点?如果存在,请求出它的解析式;如果不存在,请说明理由.

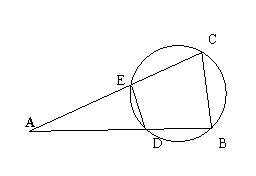14．如图，在中，AB=5，AC=7.点D在AB上由A向B移动（D不与A、B重合）过B、C、D三点作一个圆交AC于点E，设AD=，CE=，求关于的函数关系式，并指出该函数中自变量的取值范围.

 

15.某移动通讯公司开设了两种通讯业务,“全球通”；使用者先缴50元月租费，然后每通话1分钟时间，再付话费0.4元，“快捷通”；不缴月租，每通话1分钟付话费0.6元，（本题的通话均指市内通话），若一个月内通话分钟，两种方式的费用分别为元和元．

（１）写出、之间的函数关系式；

（２）一个月通话多少分钟，两种移动通讯费用相同？

（３）某人估计一个月通话时间为300分钟，应选择哪种移动通讯合算些？

16已知反比例函数）和一次函数.

（1）如果一次函数和反比例函数的图象交于点(-3,),求和的值;

（2）当满足什么条件时,这两个函数的图象有两个不同的交点?

（3）当=-2时,设(2)中的两个函数图象的交点分别为A、B,试判断此时Ａ、Ｂ两点在第几象限？是锐角还是钝角（只要求直接写出结论）？

参考答案:

1.B　 2.D　 3.B　 4.D　 5.C　 6.B　 7.(3,2)　8.;　

9.(-2,5)　 　 10.两个; (-2,0)　(1,0)　　11 .-3;-2　

12.　　 13 .存在;　　　 14.　(0<<5)　

15.(1) =50+0.4 ,　=0.6

(2)当=时,,所以一个月内通话250分,两种方式的移动通话费用相同.

(3)当,=170,　=180,所以估计一个月通话300分,使用“全球通”合算.

16.（１） ；＝９；（２）9且；（3）钝角。毛