1、(2005天津)若关于x的一元二次方程2x2-2x+3m-1=0的两个实数根x1,x2,且x1·x2>x1+x2-4,则实数m的取值范围是 D
(A)m>![]() (B) m≤
(B) m≤![]()
(C) m<![]() (D)
(D) ![]() <m≤
<m≤![]()
2、(2005天津)解方程组 ![]()
3、已知![]() 是一元二次方程
是一元二次方程![]() 的两个实根。
的两个实根。
(1)求实数![]() 的取值范围;
的取值范围;
(2)如果![]() 满足不等式
满足不等式![]() ,且
,且![]() 为整数。求
为整数。求![]() 的值。
的值。
解:(1)当![]() 时,方程
时,方程![]() 有实数根(2)m= -2,-1
有实数根(2)m= -2,-1
4、(淄博市2004).若关于x的一元二次方程![]() 有实数根,则k的取值范围是D
有实数根,则k的取值范围是D
(A)k>-1 (B)k≥-1
(C)k>-1且k≠0 (D)k≥-1且k≠0
5、(2004年湖北省襄樊)已知关于![]() 的方程
的方程![]() 有两个实数根.
有两个实数根.
(1)
求![]() 的取值范围;
的取值范围;
(2) 若方程的两个实数根的平方和为6,求m的值.
解:(1)由题意,得 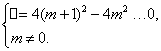
解之,得![]()
(2)设原方程的两个根为α、β,则
![]()
依题意,得![]()
∴![]()
即![]()
解之,得 ![]()
∵![]()
∴![]()
6、(2004年湖北省襄樊)汉江上游的某一牧场有162公顷,为了改善流域环境,把一部分牧场改为林场,改造后牧场面积是林场面积的20%,则退牧还林后,林场面积为__.135 __公顷.
7、(2004年湖北省襄樊)二元二次方程组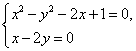 的解是_
的解是_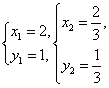 _____.
_____.
8、(遂宁市2004)解方程:![]() .
.![]()
![]()
9、(遂宁市2004)已知关于x的一元二次方程![]()
(1) 试判断此一元二次方程根的存在情况;
(2) 若方程有两个实数根![]() ,且满足
,且满足![]() ,求k的值.
,求k的值.
(1)∵△
∴此一元二次方程有两个不相等的实数根
(2)k=2
10、(泰州2004)四边形ABCD中,AB∥CD,且AB、CD长是关于x的方程![]() 的两个实数根,则四边形ABCD是C
的两个实数根,则四边形ABCD是C
A. 矩形 B. 平行四边形 C. 梯形 D. 平行四边形或梯形
11、(泰州2004)用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.
 |
(1)用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.
(2)若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程![]() 的两个实数根,试求出原矩形纸片的面积.
的两个实数根,试求出原矩形纸片的面积.
(1)(画对1个得2分,共4分)
(2)由题可知AB=CD=AE,又BC=BE=AB+AE
∴BC=2AB, 即![]()
由题意知 ![]() 是方程
是方程![]() 的两根
的两根
∴![]()
消去a,得 ![]() 解得
解得 ![]() 或
或![]()
经检验:由于当![]() ,
,![]() ,知
,知![]() 不符合题意,舍去.
不符合题意,舍去.
![]() 符合题意.
符合题意.
∴![]()
12、(安徽理科实验班2004)若![]() 是方程
是方程![]() 的根,则
的根,则![]() 的值为 【 C 】
的值为 【 C 】
A.0 B.1 C.-1 D.2
13、(安徽理科实验班2004)设![]() 为正整数,若
为正整数,若![]() 是完全平方数,则它前面的一个完全平方数是
【 D 】
是完全平方数,则它前面的一个完全平方数是
【 D 】
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
※※※14、(安徽理科实验班2004)甲、乙两个粮库原来各存有整袋的粮食,如果从甲库调90袋到乙库,则乙库存粮是甲库的2倍;如果从乙库调若干袋到甲库,则甲库存粮是乙库的6倍.问甲库原来最少存粮多少袋?
解:设甲库原来存粮![]() 袋,乙库原来存粮
袋,乙库原来存粮![]() 袋,依题意可得
袋,依题意可得
![]() . (1)
. (1)
再设乙库调![]() 袋到甲库,则甲库存粮是乙库的6倍,即
袋到甲库,则甲库存粮是乙库的6倍,即
![]() .
(2)
.
(2)
由(1)式得
![]() .
(3)
.
(3)
将(3)代入(2),并整理得
![]() .
由于
.
由于![]() .
.
又![]() 、
、![]() 是正整数,从而有
是正整数,从而有![]() ≥1,即
≥1,即![]() ≥148;
≥148;
并且7整除![]() ,又因为4与7互质,所以7整除
,又因为4与7互质,所以7整除![]() .
.
经检验,可知![]() 的最小值为152.
的最小值为152.
答:甲库原来最少存粮153袋.
15、(2004年苏州)已知关于x的一元二次方程 ax2+x—a=0 ( a≠0 )
(1) 求证:对于任意非零实数a,该方程恒有两个异号的实数根;
(2) 设x1、 x2是该方程的两个根,若∣x1∣+ ∣x2∣=4,求a的值。
(1)证明:∵⊿=1+4a2, ∴⊿>0 ∴方程恒有两个实数根
设方程的两根为x1,x2, ∵a≠0, ∴x1·x2= —1<0
∴方程恒有两个异号的实数根
(2)∵x1·x2<0, ∴∣x1∣+∣x2∣=∣x1 — x2∣=4
x1+x2(x1+x2)2 — 4x1 x2=16
又∵x1+x2= —![]() , ∴
, ∴![]() +4=16。∴a=±
+4=16。∴a=±![]()
16、(绍兴市2004)已知一元二次方程![]() 的两个根满足
的两个根满足![]() ,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.小敏解得此题的正确答案“∠B=120°”后,思考以下问题,请你帮助解答.
,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.小敏解得此题的正确答案“∠B=120°”后,思考以下问题,请你帮助解答.
(1) 若在原题中,将方程改为![]() ,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的
,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的![]() 的值作怎样的改变?并说明理由.
的值作怎样的改变?并说明理由.
(2) 若在原题中,将方程改为![]() (n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的
(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的![]() 的值应改为多少(不必说明理由)?
的值应改为多少(不必说明理由)?
(1)∵ ∠B=120°,a=c, ∴ b=![]() a,△=5a2>0.
a,△=5a2>0.
又∵ ![]() =
=![]() =
=![]() . ∴
. ∴ ![]() =
=![]() .
.
(2)![]() =
=![]() .
.
17、(绍兴市2004)化简:⑴![]() ;⑵若m,n是方程x2-3x+2=0的两个实根,求第(1)小题中代数式的值.
;⑵若m,n是方程x2-3x+2=0的两个实根,求第(1)小题中代数式的值.
(1)![]() =
=![]() .
.
(2)∵ m+n=3,m·n=2, ∴![]() =
=![]() =
=![]() .
.
18、(陕西省2004)在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是【 B 】
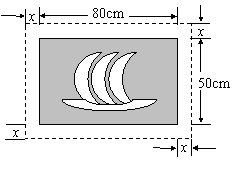 A.x2+130x-1400=0
B.x2+65x-350=0
A.x2+130x-1400=0
B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
19、(陕西省2004)解方程:![]()
解:去分母,得

20、(连云港市2004)某种商品进价为a元/件,在销售旺季,商品售价较进价高30%;销售旺季过后,商品又以7折(即原售价的70%)的价格开展促销活动,这时一件该商品的售价为D
(A) a元 (B)0.7 a元 (C)1.03 a元 (D)0.91a元
21、(连云港市2004)关于x的一元二次方程![]() 有实数根,则k的取值范围是 B
有实数根,则k的取值范围是 B
(A)![]() (B)
(B)![]() ≤
≤![]() (C)
(C)![]() (D)
(D)![]() ≥
≥![]()
22、(2004年龙岩)已知关于x的方程![]() 的两实根x1、x2满足: x1+ x2=2,试求k的值.
的两实根x1、x2满足: x1+ x2=2,试求k的值.
解法一:依题意,![]() ,所以x1与x2同号……(2分)
,所以x1与x2同号……(2分)
1. 当x1>0,x2>0时,有x1+ x2=2,即k+1=2,k=1无解。
2. 当x1<0,x2<0时,有-( x1+ x2)=2,即k+1=-2,k=-3…………………………(6分)
Δ=[-4(k+1)]2-16(k2+1)=32k ………………………………………………………(7分)
当k =1时,Δ>0符合题意;
当k =-3时,Δ<0舍去。
所以,满足题意的k的值为1………………………………………………………(10分)
解法二:依题意,Δ=[-4(k+1)]2-16(k2+1)=32k≥0,即k≥0………………(2分)
于是x1+ x2=k+1>0………………………………………………………………(4分)
又![]()
∴x1>0,x2>0……………………………………………………………………(7分)
由 x1+ x2=2,得x1+ x2=2
k+1=2,解得k=1。
所以,满足题意的k的值为1。
23、(2004年龙岩) 某商品标价1200元,打八折售出后仍盈利100元,则该商品进价是B
(A)800元 (B)860元 (C)900元 (D)960元
24、(南昌市2004)已知关于x的方程x2-2(m+1)x+m2=0.
(1)当m取什么值时,原方程没有实数根;
(2)对m选取一个合适的非零整数,使原方程有两个实数根,并求这两个实数根的平方和.
解:(1)△=[-2(m+1)]2-4m2 ………………………………………………………1分
=4(m2+2m+1)-4m2
=4(2m+1)<0. ……………………………………………………… 2分
∴m<-![]() .
.
当m<-![]() 时,原方程没有实数根; …………………………………………………3分
时,原方程没有实数根; …………………………………………………3分
(2)取m=1时,原方程为x2-4x+1=0.…………………………………………………4分
设此方程的两实数根为x1, x2,则x1+x2=4, x1·x2=1.…………………………………5分
∴x12+x22=(x1+x2)2-2x1x2=42-2×1=14.
25、(2004年南通)解方程组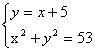
26、(2004年南通)已知关于x的一元二次方程![]()
⑴请选取一个你喜爱的m的值,使方程有两个不相等的实数根,并说明它的正确性;
⑵设x1,x2是⑴中所得方程的两个根,求x1x2+x1+x2的值。
所取m值要满足m>![]() 下略
下略
※※※27、(淮安市2004) 如图①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,如图①,在盒子的内部我们先取棱BB1的中点E,
再连结AE、EC1.昆虫乙如果沿路径A—E—C1爬行,那么可以在最短的时间内捕捉到昆虫
甲.仔细体会其中的道理,并在图①中画出另一条路径,使昆虫乙从顶点A沿这条路径爬行,同样可以在最短的时间内捕捉到昆虫甲.(请简要说明画法)
(2)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1秒)

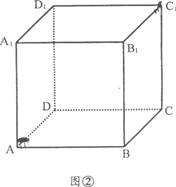
![]()
别为各棱中点) (说明:无画法,扣2分)
(2)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四
种路径中的任意一种爬行:
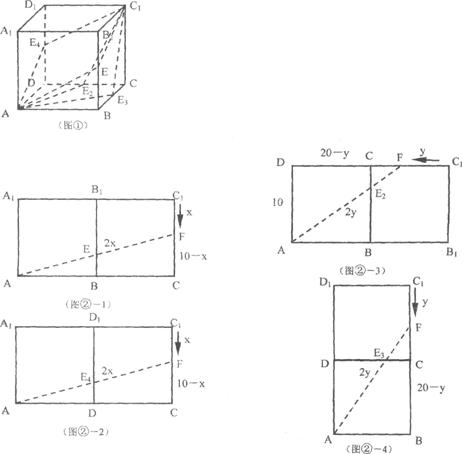
可以看出,图②-1与图②-2中的路径相等,图②-3与图②-4中的路径相等.
①设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F
爬行捕捉到昆虫甲需x秒钟,如图②-1-1,在Rt△ACF中,
(2x)2=(10-x)2+202,解得x=10;
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F
爬行捕捉到昆虫甲需y秒钟,如图②-1-2,在Rt△ABF中,
(2y)2=(20-y)2+102,解得y=8;
所以昆虫乙从顶点A爬行捕捉到昆虫甲至少需8秒钟.
【说明】未考虑到A→E→F和图④中其它路径,而直接按路径A→E→F(或A→E→F)
计算,并求出正确答案的不扣分.
28、(日照市2004)方程组 只有一个实数解,则实数
只有一个实数解,则实数![]() 的值是 -1/6 ,-1/2,0
的值是 -1/6 ,-1/2,0
29、(郴州市2004)方程![]() 的左边配成完全平方后所得方程为 ( A )
的左边配成完全平方后所得方程为 ( A )
A. ![]() B.
B. ![]() C.
C. ![]() D. 以上答案都不对
D. 以上答案都不对
30、(郴州市2004)今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.
(1)求降低的百分率;(2)若小红家有4人,明年小红家减少多少农业税?(3)小红所在的乡约有16000农民,问该乡农民明年减少多少农业税.
(1)设降低的百分率为x,
依题意有 解得x1=0.2=20%,x2 =1.8(舍去)
(2)小红全家少上缴税 25×20%×4=20(元)
(3)全乡少上缴税 16000×25×20%=80000(元)
31、(2004年富阳)解下列方程:
(1)![]() (2)
(2)![]()
32、(2004年富阳)已知一个长方体的木箱高为80![]() ,底面的长比宽多10
,底面的长比宽多10![]() ,(1)求这个长方体的体积
,(1)求这个长方体的体积![]() (
(![]() )与长方体的宽
)与长方体的宽![]() (
(![]() )之间的函数关系式;(2)问当该木箱的体积为0.72
)之间的函数关系式;(2)问当该木箱的体积为0.72![]() 时,木箱底面的长与宽各为多少
时,木箱底面的长与宽各为多少![]() ?
?
解:(1)因为木箱的长、宽、高分别为:![]()
![]() 、
、![]()
![]() 、80
、80![]() ……2分
……2分
所以 ![]()
(2)因为 0.72![]() =720000
=720000![]()
所以 ![]() 即
即 ![]()
解得:![]() (舍去)
(舍去)![]()
![]()
所以当木箱体积为0.72![]() 时,底面的长和宽分别为100
时,底面的长和宽分别为100![]() 和90
和90![]() 。
。
33、(湖州市2004)方程组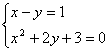 的解是(B )
的解是(B )
![]()
34、(河南2004)已知![]() ,
,![]() ,试判断关于
,试判断关于![]() 的方程
的方程![]() 与
与![]() 有没有公共根。请说明理由。
有没有公共根。请说明理由。
不妨设关于![]() 的方程
的方程![]() 与
与![]() 有公共根,设为
有公共根,设为![]() ,则有
,则有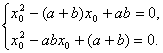
整理可得 ![]() 。
。
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() 。把
。把![]() 代入①得
代入①得![]() ,这是不可能的。所以关于
,这是不可能的。所以关于![]() 的两个方程没有公共根。
的两个方程没有公共根。
35、(2004年福建三明)已知关于x的方程![]() (m为正整数)有两个实数根
(m为正整数)有两个实数根
x1,x2,分别求下列两式的值:
(1)(x1-1)(x2-1); (2)![]() .
.
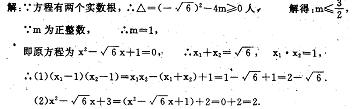
36、(云南省2004)将二次三项式![]() 进行配方,正确的结果应为( C )
进行配方,正确的结果应为( C )
A、![]() B、
B、![]() C、
C、 ![]() D、
D、 ![]()
37、(福州2004)已知一元二次方程![]() .
.
⑴ 当![]() 取何值时,方程有两个不相等的实数根?
取何值时,方程有两个不相等的实数根?
⑵ 设![]() ,
,![]() 是方程的两个实数根,且满足
是方程的两个实数根,且满足![]() ,求
,求![]() 的值.
的值.
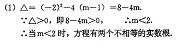
![]()