天门市2005年中考试卷

数学

亲爱的同学们，发挥你的聪明才智，展示你的鲜明个性，抒写你的独特见解，这份试卷将再次记录你的自信、沉着、智慧和收获。别忘了以下注意事项：

1．　本卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)，第Ⅰ卷1至2页，第Ⅱ卷3至8页，满分120分，考试时间120分钟。

2．　答第Ⅰ卷前，考生务必用钢笔(圆珠笔)将自己的姓名，用2B铅笔将准考证号、考试科目写或涂在答题卡上。

3．　第Ⅰ卷每小题选出答案后，用2B铅笔将答题卡上对应题目的答案号涂黑。如需改动，用4B橡皮擦干净后，再涂选其它答案。答案写在第Ⅰ卷上无效。

4．　答第Ⅱ卷时，将答案直接写在试卷上。

5．　考试结束，考生须将第Ⅰ卷、第Ⅱ卷和答题卡一并交回。

第Ⅰ卷 （选择题 共36分）

一、选择题(本大题共12个小题，每小题3分，共36分)

下列各题四个选项中，仅有一个正确，在答题卡相应的题号上将正确选项涂黑。

1．  下列各组数中，互为相反数的是

A.8和－　　 B. 8和　　 C.8和－8　　 D.8和

2．十届人大三次会议温总理在政府工作报告中指出，今年中央财政将安排万元解决下岗工人的再就业问题，这个数字用科学记数法表示为

A.109×10⁴万元　　 B.1.09×10⁴万元　　 C.1.09×10⁵万元　　D.1.09×10⁶万元

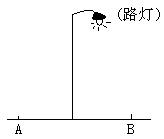3．一天晚上，小奇在路灯下散步(如图)，当他从A处走到B处这一过程中，他在地上的影长的变化情况为

A.逐渐变长　　 B.逐渐变短　　 C.先变长后变短　　 D.先变短后变长

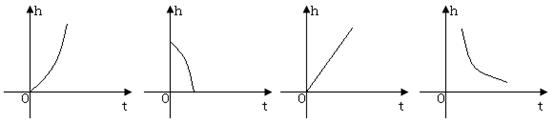
4．一个熟透的苹果从树上自由落下，在下落的过程中，它下落的高度h与下落的时间t的函数关系式为(g是大于0的常数)，则下列选项中能表示其函数关系的大致图像是

A.　　　　　　　　  B.　　　　　　　　  C.　　　　　　　　  D.

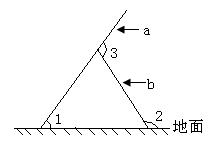
5．右图是a、b两片木板放在地面上的情形。图中∠1、∠2分别为a、b两木板与地面的夹角，∠3是两木板间的夹角。若∠3＝110°，则∠2－∠1等于

A.55°　　 B.70°　　 C.90°　　 D.110°

6．下列关于的叙述，不正确的是

A.是方程 ＝10的一个解　　　　　　　 B.在数轴上可以找到表示的点　　

C. ＝2　　　　　　　　　　　　　　  D. ＜4

7．下面四个平面图形折叠后，能得到的是

　

A.　　　　　　  B.　　　　　　　 C.　　　　　　  D.

8．为了了解秦兵马俑的身高状况，某考古队随机调查了8尊秦兵马俑雕塑，它们的高度(单位：厘米)如下：172，187，184，184，181，190，187，187，这8尊兵马俑的高度的众数和中位数分别是

A.184，185.5　　 B.187，184　　 C.190，185.5　　 D.187，185.5

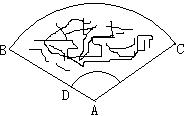9．如图，一扇形纸扇完全打开后，外侧两根竹条AB和AC的夹角为120°，AB长为9，贴纸部分的宽BD为6，则贴纸部分面积(贴纸部分为两面)是

　

A.24π　　 B.36π　　C.48π　　D.72π

10．已知点(－2，a)，(2，b)，(4，c)在反比例函数的　图像上，则a、b、c的大小关系为

A.a＞b＞c　　 B. a＞c＞b　　 C.c＞b＞a　　 D.c＞a＞b

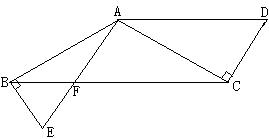
11．如图，∠ABC=∠ACB,CD⊥AC于C,BE⊥AB 于B，AE交BC于F，且BE=CD，下列结论不一定正确的是

A.AB=AC　　B. ∠BAE=∠CAD　　 C.AE=AD　　　　 D.BF=EF

12．观察判断：如图，若对应，那么对应

　　　A.　　　　　　　 B.　　　　　　  C.　　　　　　　　 D.

第Ⅱ卷 （非选择题 共84分）

二、填空题(本大题共5个小题，每小题3分，共15分)

13．方程的解为　　　　　　　　　  。

14．写出一个图象不经过第三象限的一次函数的解析式　　  　　　。

15．如图，已知登山缆车行驶路线与水平线间的夹角α=30°，β=45°。小勇乘缆车上山，从A到B，再从B到D均走了100米(即AB=BD=100米)，则缆车垂直上升的高度DE为  米。(结果保留根号)

16．“五·一”节期间，某商场为吸引顾客，实行“买100送20，连环送”的活动，即顾客购物满100元，就可以获赠商场购物券20元，不足100元的部分不赠券，并且购物可以用现金，也可以用购物券。如果你有340元现金，在活动期间到该商场购物，最多可以获赠购物券累计为　　　　　　  　 元。

17．如图，右边①、②、③、④四个大正方形都是由四个边长为1的小正方形组成的，请你仔细观察，其中阴影部分面积最大的图形是　　　　 。(填序号)

　　

　　　 ①　　　　 ②　　　　 ③　　　　 ④

三、解答题(本大题共8个小题，共69分)

18．(本小题满分7分)

　　计算：

19．(本小题满分7分)

　　解不等式组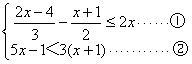，并把它的解集在数轴上表示出来。

20．(本题共2个小题，其中第<1>小题3分，第<2>小题4分，满分7分)

　　(1)连续两次掷一枚均匀的骰子，则两次所掷骰子的点数和为8的概率是　　　 (直接写出结果)。

　　(2)如图，广宇购物中心设立了一个可以自由转动的转盘，并规定：顾客购物20元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品。下表是活动进行中的一组统计数据。

转动转盘的次数n	100	200	400	500	1000
落在“牙膏”的次数m	58	58	121	149	300
落在“牙膏”的频率			0.3025

①　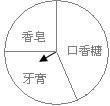　 计算并完成上面的表格

②　　 请估计，当n很大时，频率将会接近多少？

③　　 假如你去转动该转盘一次，你获得牙膏的概率时多少？

21．(本小题满分7分)

为“保护环境，绿化江河”，植树节这天，某中学八年级(一)、(二)、(三)班的学生积极参加植树活动。已知该校八年级共有3个班，且这三个班共有学生200人。根据右图所给信息解答：

(1)八年级(三)班共有多少学生？

(2)这三个班共植树多少课？

  　

22．(本小题满分8分)

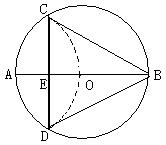
如图，斌斌要在一块圆形纸板中尽量不浪费地裁剪出一个等边三角形；他是这么做的：先画⊙O的直径AB，再将图形折叠，使A点与O点重合，折痕CD交AB于E。

　  (1)判断以A、D、O、C为顶点的四边形是什么四边形？　　　　　　  (将结果直接写在横线上)

　　(2)求证：△CDB是等边三角形。

　 

23．“六·一”儿童节期间，某超市将销售价为每个30元的某种儿童玩具实行降价促销，在促销中发现，当每个玩具的销售价降低x元时，日销售量y(个)与x(元)之间满足关系式。已知超市购进这种玩具所需成本为每个10元。

(1)用含x的代数式表示：降价后，每个玩具的实际销售价为　　　　　  元，每个玩具的利润为　　　　　  元；

(2)设降价后该玩具每日的销售利润为W元，求W与x之间的函数关系式；

(3)若规定每个玩具的降价不得超过10元，试问：当该玩具的日销售量最大时，每日的销售利润能否也最大？为什么？

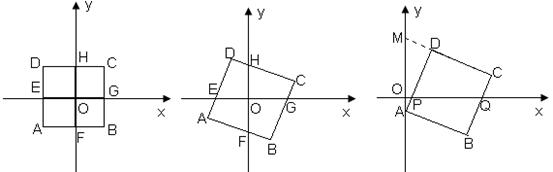
24．如图，在平面直角坐标系中，正方形ABCD的边DA、AB分别垂直于x轴、y轴，原点O在正方形ABCD的对称中心，正方形各边分别交坐标轴于E、F、G、H四点

　  (1)EG与FH有何数量关系，直接写出你的猜想为：　　　　　　　　　

　  (2)将图①中的正方形ABCD绕原点O顺时针旋转角()，如图②。请问：你在(1)中猜想的结论还成立吗？说明理由。

　  (3)将图②中的正方形ABCD沿x轴向右平移，使原点O落在正方形ABCD的外部，点A落在y轴上，CD的延长线交y轴于点M，AD、BC分别交x轴于点P、Q，如图③。已知A点坐标为（0，－1），M点坐标为（0，4）。请你在直线BC上找出一点T，使T到AM的距离等于PQ的长，并求出直线OT的解析式。

25．(本小题满分12分)

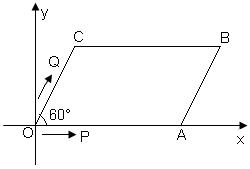
如图，□OABC在直角坐标系中，O为坐标原点，OA在x轴正半轴上，OA＝8，OC＝4，∠COA=60°。点P、Q同时从原点出发，分别作匀速运动，其中点P沿OA向终点A运动，速度为每秒1个单位，点Q沿OC、CB向终点B运动；当这两点中有一点达到自己的终点时，另一点也随之停止运动。设从出发起运动了t秒。

(1)　当点Q的速度为每秒2个单位时，试分别写出点Q在OC上、CB上时的坐标为：

　　  　　　　　　　 、　　　　　　  (用含t的代数式表示，不要求写出t的取值范围)；

(2)当以P、O、C、Q为顶点的四边形与□OABC相似时，求t的值；

(3)当点P与点Q所经过的路程之和恰为□OABC的周长的时，直线PQ把□OABC分割成左、右两部分。试问：其左边部分的面积能否也为□OABC面积的，如有可能，请求出相应的t值；如不可能，说明理由。