2006年九年级数学模拟考试试卷

（考试时间：120分钟，满分：150分）

注意：1、本试卷分第一部分选择题和第二部分非选择题．

2、所有答案写在答题卷的相应位置上，可以使用计算器．

参考公式：二次函数y=ax²+bx+c的顶点坐标是．

　试 卷 Ⅰ

一、选择题（本题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

1. －的相反数是（　　）

A、2　　　 B、－2　　　 C、　　　　D、－

2. 为了迎接2008年奥运会在中国北京举行，北京市现在执行严格的机动车尾汽排放标准，同时正在设法减少工业及民用燃料所造成的污染，随着每年10亿立方米的天然气输送到北京，这样，到2006年底，北京的空气质量将会基本达到发达国家城市水平，10亿用科学记数法可以表示为（　　 ）

A、 1.0×10　　 B、 1.0×10　　 C、 1.0×10　　 D、1.0×10

3．一张桌子上摆放着若干个碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有碟子为（　　）

A、6个 　　　　  B、8个　　　　　 C、12个 　　　　　　　D、17个

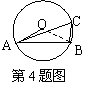
4. 如图，A、B、C为⊙O上三点，如果∠OAB=46°，则∠ACB度数为（　　）

　 A、44°　　　　　　B、92°　　　 C、80°　　　　　　　　 D、46°

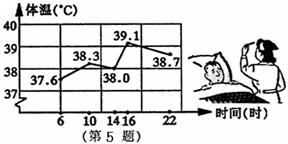
5．如图是护士统计一位病人的体温变化图，这位病人中午12时的体温

约为　 （　　）　　　　　　　　　　　　　　　　　　　　　　　

A、39.0℃　　 B、38.5℃　　　C、38.2℃　 　　　D、37.8℃

6．某校九年级毕业时,每一个同学都将自己的像片向全班其他同学各送一张表示留念全班共送了1960张像片,如果全班有x名学生,根据题意列出方程为（　 　）

A、x (x-1)= 1960　　　　　B、x (x-1)= 1960×2　

C、2x (x+1)= 1960　 　　　D、x (x+1)= 1960

7.某地区为估计该地区麋鹿的只数，先捕捉20只麋鹿给它们分别作上标志，然后放回，待有标志的麋鹿完全混合于麋鹿群后，第二次捕捉40只麋鹿，发现其中两只有标志.从而估计该地区有麋鹿（　　）

A、200只　　　　  B、400只　　　　 C、800只　　　　　  D、1000只

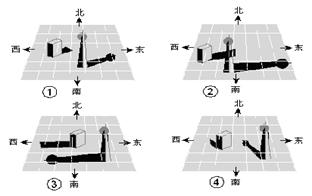
8.下面是一天中四个不同时刻两个建　筑物的影子，将它们按时间先后顺序进行排列，正确的是（　　 ）

A、③④①②　  B、②④③①

C、③④②①　  D、③①②④

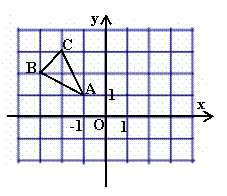9．如图，若将△ABC绕点A顺时针旋转90°后得到△，则B点的对应

点B′的坐标是（　　）

A、（－3，－2）　　　　B、（2，2）　　

C、（0，3）　　　　　 D、（2，1）

 

10．如图：向放在水槽底部的烧杯注水（流量一定），注满烧杯后，继续注水，直至注满水槽，水槽中水面上升高度与注水时间之间的函数关系大致是下列图象中的（　　）

	第10题图

1

试 卷 Ⅱ

二、填空题（本题有6小题，每小题5分，共30分）

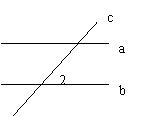
11.　如图，直线a,b被直线c所截，a∥b，

第11题图

如果∠1=50°，那么∠2=____度．

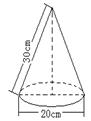
12.　右图是小明制作的一个圆锥形圣诞帽的示意图围成

第12题图

这个纸帽的纸的面积为_______cm²．

13. 写出一个顶点坐标为（2，1）的抛物线的关系式　　　　　　　　　　　  ．

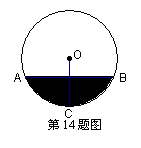14. 如图，半径是13cm圆柱形油管内装入油，油深CD为8cm，

那么油面宽度AB=　　　cm．

15.　指令(S,Q)的意义：以原地原方向为基准，沿逆时针方

向旋转Q角，再沿旋转后的方向行进S米，现有一位于

A点处的机器人，面朝正东方向，按指令(5,60^o)运动至B 点，再按指令(5,120^o)运动至C点，则AC=　　　　米.

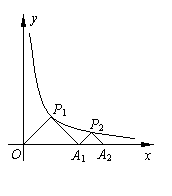
16.　如图，△P₁OA₁、△P₂A₁A₂都是等腰直角三角形，且点P₁、P₂在函数y＝(x＞0)的图像上，斜边OA₁、A₁A₂都在x轴上，则点A₂的坐标是　　　　  　　 .

	第16题图

三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）

17.　(1) 计算：－　　　　　  (2) 解方程：2x²－4x-1=0

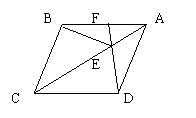18. 已知：如图，四边形ABCD是菱形，F是AB上一点，DF交AC于E.

求证：∠AFD＝∠CBE

	第18题图

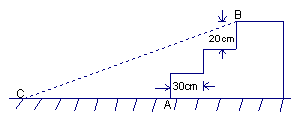19.　如图，某公园入口处原有三阶台阶，每级台阶高为20cm,深为30cm,为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度.（精确到1 cm）

	第19题图

20.　如下图，由小正方形组成的L形图中，请你用三种方法分别在下图中添画一个小正方形使它成为轴对称图形：

方法一　　　　 方法二　　　　 方法三

21.　一辆汽车要将一批10㎝厚的木板运往某建筑工地，进入工地到目的地前，遇有一段软地．聪明的司机协助搬运工将部分木板卸下铺在软地上，汽车顺利通过了．

⑴ 请你写出其中的道理：　　　　　　　　　　　　　　　　　　 ．如果卸下部分木板后汽车对地面的压力为3000N，若设铺在软地上木板的面积为S㎡，汽车对地面产生的压强为P（N/㎡），那么P与S的函数关系式是　　　　　　 ．

请在直角坐标系中，作出相应的函数图象．

⑵ 若铺在软地上的木板面积是30㎡，则汽车对地面　的压强是　　　　　　 N/㎡．

⑶ 如果只要汽车对地面产生的压强不超过600N/㎡，汽车就能顺利通过，则铺在软地上的木板面积最少要　　　　 ㎡．

22. “温州五马美食”食品有限公司推出一种新款美食，定价50元/份．总经理准备开展“新款美食促销活动”广泛征求职工的意见．甲职工认为可以打折销售，每份美食打8折；乙职工认为可用有奖销售，具体办法是：顾客每消费一份美食，获得一次抽奖的机会，让顾客从一个内装大小、形状、质量完全相同的3个黑球和2个红球的袋中摸出2个球，奖励办法是①摸出2个全是红球为一等奖，顾客免费享用美食，②摸出2个全是黑球为二等奖，顾客获得优惠10元，③摸出1红1黑为三等奖，顾客获得优惠2元 ．经调查发现两种促销办法的销量将会相同，你认为哪种促销方案对公司有利？为什么？请用所学的数学知识加以说明．（要有必要的计算过程）

23. 我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积．用现代式子表示即为：

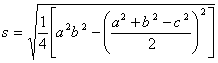 ……①（其中、、为三角形的三边长，为面积）.

而另一个文明古国古希腊也有求三角形面积的海伦公式：

　　 ……②（其中）.

（1） 若已知三角形的三边长分别为5、7、8，试分别运用公式①和公式②，计算该三角形的面积；

（2）你能否由公式①推导出公式②？请试试.

24.　图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）.

（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连结AD、BE，CE的延长线交AB于F（图2）；

探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论.

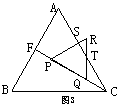
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；

探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围.

（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（30°＜α＜90°）（图4）；

探究：在图4中，线段C′N·E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N·E′M的值，如果有变化，请你说明理由.

2006年九年级数学模拟考试（参考答案）

参考答案和评分标准

一、选择题(本题有10小题，每小题4分，共40分)

题号	1	2	3	4	5	6	7	8	9	10
答案	C	A	C	D	C	A	B	A	C	B

二、填空题(本题有6小题，每小题5分，共30分)

11　50　　12　　　13　答案不惟一　　14　 15　5　　16　

三、解答题(本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分)

17　解：(1) -=……(每项算对，各给1分)……3分

　　　 　　 =．…………………………………………………………………… 1分

（注：用计算器求解正确或只写答案均给3分）

　　(2) a=2,b=－4,c=－1,△=b²－4ac=16+8=24……………………………………………１分

∴ x=…………………………………………………………3分

18　证：　∵ 菱形ABCD，

∴ AB∥CD， CB=CD,∠BCE=∠DCE………………………………………1分

∴　∠AFD=∠CDE ．…………………………………………1分

∵　CE=CE，

∴　△BCE≌△DCE．……………………………………………2分

∴　∠CBE=∠CDE．……………………………………………………2分

∴　∠AFD=∠CBE．…………………………………………………………2分

19　解：过点Bz作BD⊥CB于点D，则…………………………………………………1分

　　　　  BD=60,AD=60,∠BDC=90°……………………………………………………2分

∴ CD=………………………………………2分

∴ CA＝CD－AD=2823－60=2223≈222(㎝)…………………………………2分

答：AC的长为222㎝.…………………………………………………………1分

20　拼对第一个2分，后两个各3分，共8分，不同的拼法例举如下：

21　解：（1）压强原理（减小压力和增大受力面积来减小压强）…………………………2分

P= ………………………………………………………………………2分

图像………………………………………………………………… ………2分

（2）100………………………………………………………………………………2分

（3）5………………………………………………………………………………2分

22　解：由于两种促销方法的销量相同，不妨设都销售了x份

在甲职工的建议下，公司让利为…………………………………2分

在乙职工的建议下，P(获一等奖)= …………………………………2分

P（获二等奖）=…………………………………………………………2分

P（获三等奖）= ………………………………………………………2分

这样公司让利为…………………………2分

由于，即相同的销量但乙职工的建议使得公司让利少于甲职工，从经济方面考虑乙职工的促销方案对公司有利……………………………………………………2分

 

23、　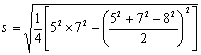　 ……………………………1分

　　　　　　　　  ；　　………………………2分

又　 ，　　　……………………………………1分

∴　 .  …2分

⑵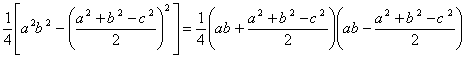…2分

　　　　　

　　　　　 　　　 ………………2分

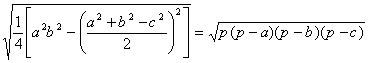　　　 ……………………………………1分

∴ 　　　…1分

（说明：若在整个推导过程中，始终带根号运算当然也正确。）

24、解（1）BE=AD………………………………………………………………1分

　　　 证明：∵△ABC与△DCE是等边三角形

∴∠ACB=∠DCE=60° CA=CB，CE=CD…………………………………1分

∴∠BCE=∠ACD　∴△BCE≌△ACD……………………………………1分

　　　　　　　 ∴ BE=AD…………………………………………………………………1分

（也可用旋转方法证明BE=AD）

（2）　　　　　　　　 如图在△CQT中 ∵∠TCQ=30° ∠RQT=60°

　　　　　　　　　　　∴∠QTC=30° ∴∠QTC=∠TCQ

　　　　　　　　　　　　　　　　∴QT=QC=x

　　　　　　　　　　　　　　　　∴ RT=3－x  ……………………………………1分

∵∠RTS＋∠R=90°　　∴∠RST=90°…………………………………………1分

∴y=×3² －(3－x)²=－(3－x)²＋(0≤x≤3) ……………4分

（不证明∠RST=90°扣2分，不写自变量取值范围扣1分）

（3）C′N·E′M的值不变 ……………………………………………………1分

证明：∵∠ACC′=60°∴∠MCE′＋∠NCC′=120°

　　　　 ∵∠CNC′＋∠NCC′=120° ∴∠MCE′=∠CNC′ ……………………1分

　　　　　　 ∵∠E′=∠C′　 ∴△E′MC∽△C′CN

　　　　　 ∴　∴C′N·E′M=C′C·E′C=×=………………2分

下列各图中每个正方形网格都是由四个边长为1的小正方形组成,其中阴影部分面积是小正方形面积的的是（　　）