2005年中考第一轮复习

第六单元 生活中的平移、旋转和对称

图形的相似

Ⅰ.考点透视

一、生活中的平移、旋转和对称

1.平移(平移的概念与性质)

例1、如图，由11个面积为6的等边三角形按下列方式排列，它们都有一边在同一直线上，每个三角形底边的中点恰为下一个三角形的一个顶点.

(1)请说一说该图案的形成过程；

(2)由这11个三角形所盖住的平面区域的面积是　　　　。

2.旋转(旋转的概念与性质)

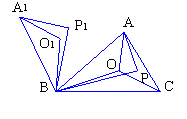
例2、如图所示，O是锐角三角形ABC内一点，∠AOB＝

∠BOC＝∠COA＝120°，P是ΔABC内不同于O的另一点；

ΔA₁BO₁、ΔA₁BP₁分别由ΔAOB，ΔAPB旋转而得，旋转

角都为60°，则下列结论：①ΔO₁BO为等边三角形，且A₁、O₁、O、C在一条直线上；②A₁O₁＋O₁O＝AO＋BO；③A₁P₁＋PP₁＝PA＋PB；④PA＋PB＋PC>OA＋OB＋OC。其中正确的有　　　　(填序号).

3.对称

(1)轴对称与轴对称图形(概念与性质)

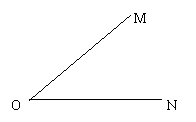
例3、已知∠MON=40°，P为∠MON内一定点，

OM上有一点A，ON上有一点B，当△PAB的周

长取最小值时，求∠APB的度数.

(2)中心对称(概念与性质)

例4、下列图形中，一定不是中心对称图形的是（　　 ）

A.至少旋转30°后才与自身重合　　 B.至少旋转60°后才与自身重合

C.至少旋转90°后才与自身重合　　 D.、至少旋转120°后才与自身重合

二、图形的相似

1.比例的性质

2.相似三角形(概念、判定与性质)

3.位似图形

例5、在如图所示的方格纸中，每个小正方形的边长都是1，若一个三角形的每个顶点都在小正方形的顶点上，则称这个三角形为格点三角形，请你在方格纸中任意画出两个相似但不全等的格点钝角三角形。

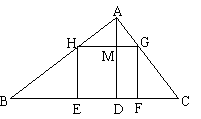例6、如果正方形的一边落在三角形的一边上，其余两个顶点分别在三角形的另外两条边上，则这样的正方形叫做三角形的内接正方形。如图，在△ABC中，BC= a，BC边上的高AD= h_a，EFGH是△ABC的内接正方形。设正方形EFGH的边长是x .

求证：

例6、已知一个二次函数的图象经过A(－1，0)，B(0，3)，C(1，4)三点.

(1)求这个函数的解析式及其顶点D的坐标；

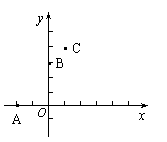(2)这个函数的图象与轴有两个交点，除点A外的另一个交点设为E，点O为坐标原点，在△AOB、△BOE、△ABE和△DBE这四个三角形中，是否有相似三角形？如果有，指出哪几对三角形相似，并加以证明；如果没有，请说明理由。

Ⅱ.中考演练

一、选择题(每小题4分，共40分)

1、下列图形中，既是中心对称图形又是轴对称图形的是

A．等腰三角形　　B．等边三角形　　C．等腰梯形　　D．菱形

2、已知a∶b=2∶3，那么(a+b)∶b等于（　　 ）

A．2∶5　　 B．5∶2　　　C．5∶3　　　D．3∶5

3、如图所示，线段AB＝CD，AB与CD相交于点O，且∠AOC＝60°，CE是由AB平移得到的，则AC＋BD与AB的大小关系是（　　 ）

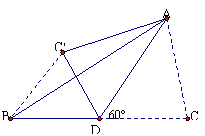A.AC＋BD<AB　　 B.AC＋BD＝AB　　 C.AC＋BD≥AB　　 D.无法确定

(第3题图)　　　　　　 (第4题图)　　　　　　　　  (第5题图)　　　　  　　　(第6题图)

4、如图所示，在ΔABC中，AD是∠BAC内的一条射线，BE⊥AD，且ΔCHM可由ΔBEM旋转而得，则下列结论中错误的是（　　 ）

A.M是BC的中点　　 B.FM＝0.5EH　　 C.CF⊥AD　　 D.FM⊥BC

5、如图AD是△ABC的中线，∠ADC=60°，BC=4，把△ADC沿直线AD折叠后，点C落在C′的位置上，那么BC′为（　　 ）

A.1　 　B.　 　C.2　　　D.

6、如图，在△ABC中，DE∥BC，DE分别与AB、AC相交于点D、E，若AD=4，DB=2，则AE︰EC的值为（　　 ）

A.0.5　　 B.2　　 C.　　 D.

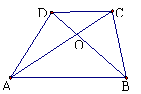
7、如图，在ABCD中，E为DC边的中点，AE交BD于点O.若S_△DOE=9，则S_△AOB等于（　　 ）

A．18　　 B．27　　 C．36　　 D．45

(第7题图)　　　　　　　  (第8题图)　　　　　　　  (第9题图)　　　　　　 (第10题图)

8、如图。ΔABC中，AE⊥BC于E，D为AB边上一点，如果BD＝2AD，CD＝8，sin∠BCD＝，那么AE的值为（　　 ）

A.3　　 B.6　　 C.7.2　　 D.9

9、如图，梯形ABCD的对角线交于点O，有以下四个结论：①⊿AOB∽⊿COD； ②⊿AOD∽⊿ACB；③S_⊿DOC∶S_⊿AOD=DC∶AB；④S_⊿AOD=S_⊿BOC。其中始终正确的有（　　 ）

A.1个　　 B.2个　　C.3个　　　D.4个

10、如图，已知边长为2的正三角形ABC中，P₀是BC边的中点，一束光线自P₀发出射到AC上的点P₁后，依次反射到AB、BC上的点P₂和P₃(反射角等于入射角)，且1<BP₃<，则PC长的取值范围是（　　 ）

A.1<P₁C<　B.<P₁C<1

C.<P₁C<　 D.<P₁C<2

二、填空题(每小题4分，共40分)

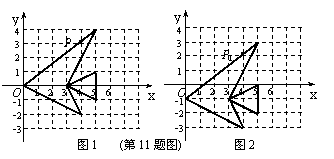
11、观察图象，与图1中的鱼相比，图2中的鱼发生了一些变化，若图1中鱼上点P的坐标为(4，3.2)，则这个点在图2中对应点P的坐标应为　　　　.

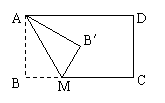
12、如图，一张长方形纸片ABCD，其长AD=a，宽AB=b(a>b)，在BC边上选取一点M，将ABM沿AM翻折后B至B′的位置，若B′为长方形纸片ABCD的对称中心，则的值是　　  .

(第13题图)　　　　　  　　　　(第14题图)　　　　　　　　　　  (第15题图)

13、矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、D为顶点的三角形与△ABM相似,则这样的点有　　　　　 个.

14、如图，AC⊥AB，BE⊥AB，AB=10，AC=2.用一块三角尺进行如下操作：将直角顶点P在线段AB上滑动，一直角边始终经过点C，另一直角边与BE相交于点D，若BD=8，则AP的长为________.

15、在方格纸中，每个小格的顶点称为格点，以格点为顶点的三角形叫做格点三角形．在如图5×5的方格纸中，以A、B为顶点作格点三角形与△OAB相似（相似比不能为１），则另一个顶点C的坐标为　　　 ．

三、(每小题8分，共16分)

16、许多几何图形是优美的。对称，就是一种美。请你运用“二个圆、二个三角形、二条线段”在下面方框内设计两幅轴对称图形，并用简练的文字说明这两幅图形的名称(或创意)。

　　　　　　　　　  名称(或创意)　　　　　　　　　　　  名称(或创意)

　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　

17、我们已经知道，如果线段MN被点P分成线段MP和PN，且，那么称线段MN被点P黄金分割，点P叫做线段MN的黄金分割点，MP与MN的比叫做黄金比。通过计算可知黄金比为。

若一个矩形的短边与长边之比等于黄金比，则称这个矩形为黄金矩形。

已知图中正方形ABCD的边长为1，请你以AD为短边，用尺规作一

个黄金矩形(要求保留作图痕迹并简要写出做法，不要求证明)。

四、(每小题9分，共18分)

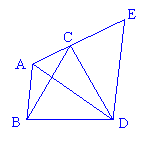18、如图所示，ΔABC中，∠BAC＝120°，以BC为边向三角形外作等边ΔBCD，把ΔABD绕着点D按顺时针方向旋转60°到ΔECD的位置。若AB＝3，AC＝2。

(1)求∠BAD的度数；

(2)求AD的长。

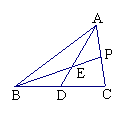19、如图，AD是ΔABC的中线，E点在AD上，BE和AC交于点P。若AP＝EP，试判断BE与AC的大小关系，并说明理由。

五、(每小题10分，共20分)

20、已知，如图所示，地面上有不在同一直线上的A、B、C三点，一只青蛙位于地面的P点，第一步青蛙从P跳到P关于A的对称点P₁，第二步从P₁跳到P₁关于B的对称点P₂，第三步从P₂跳到P₂关于C的对称点P₃，第四步从P₃跳到P₃关于C的对称点P₄，以此跳法类推，问青蛙跳完第2004步时在地面上的什么位置？

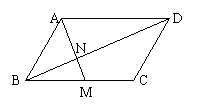21、如图，□ABCD中，M是BC的中点，AM与BD相交于点N，且AM=9，BD=12，AD=10.

求□ABCD的周长和面积.

六、(本题满分12分)

22、如果两个三角形不仅是相似三角形，而且每对对应点所在的直线都经过同一个点，那么这两个三角形叫做位似三角形，它们的相似比又称为位似比，这个点叫做位似中心．利用三角形的位似可以将一个三角形缩小或放大．

(1)选择：如图1，点O是等边三角形PQR的中心，P′、Q′、R′分别是OP、OQ、OR的中点，则△P′Q′R′与△PQR是位似三角形．此时，△P′Q′R′与△PQR的位似比、位似中心分别为（　  ）．

A．2、点P　　 B．、点P 　　 C．2、点O　　 D．、点O

图1 　　　　　　　　　　　 图2　　　　　　　　　　　  图3

(2)如图２，用下面的方法可以画△AOB的内接等边三角形．阅读后证明相应问题．

画法：①在△AOB内画等边三角形CDE，使点C在OA上，点D在OB上；

②连结OE并延长，交AB于点E′，过点E′作E′C′∥EC，交OA于点C′，

作E′D′∥ED，交OB于点D′；

③连结C′D′．则△C′D′E′是△AOB的内接三角形．

求证：△C′D′E′是等边三角形．

(3)如图3，仿上方法画△ABC的内接正方形(要求：写出画法，勿需证明).

七、(本题满分12分)

23、如图，有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板PHF的直角顶点P落在AD边上（不与A、D重合），在AD上适当移动三角板顶点P：

(1)能否使你的三角板两直角边分别通过点B与点C？若能，请你求出这时AP的长；若不能，请说明理由。

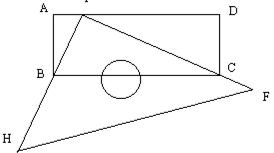(2)再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于点E，能否使CE＝2cm？若能，请你求出这时AP的长；若不能，请你说明理由。

八、(本题满分12分)

24、已知：如图，等边三角形ABC的边长为6，点D，E分别在边AB，AC上，且AD＝AE＝2。若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动，设点F运动的时间为t秒。当t＞0时，直线FD与过点A且平行于BC的直线相交于点G，GE的延长线与BC的延长线相交于点H，AB与GH相交于点O。

（1）设△EGA的面积为S，写出S与t的函数关系式；

（2）当t为何值时，AB⊥GH；

（3）请你证明△GFH的面积为定值；

（4）当t为何值时，点F和点C是线段BH的三等分点。