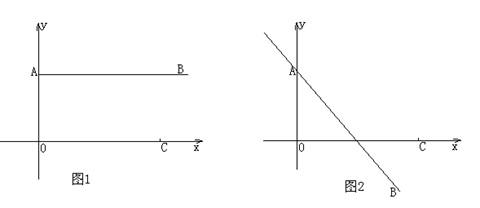初三数学第二学期阶段性质量检测试卷

温馨提示：用心思考，细心答题，相信自己会有出色的表现！

一、　　　　　  选择题（本题共10小题，每小题4分，共40分）

1. 我国股市今年连创新高，据中国证券结算公司统计，A股一季度开户总数超过去年总开户数达474万户，这个数用科学记数法表示为：　　　　　　　　　　　　　　　 (　　　)

　 A. 4.74×10²　　 B. 4.74×10⁶　　C. 474×10⁴　　D. 4.74×10⁵

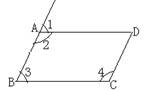2. 如图， 在平行四边形ABCD中，下列各式不一定正确的是：　　　　　　　 (　　　)

　 A. ∠1+∠2=180⁰　　　 B. ∠2+∠3=180⁰　

　 C. ∠3+∠4=180⁰　　　D. ∠2+∠4=180⁰

3. 已知⊙O₁和⊙O₂ 的半径分别为3和4 ， 且O₁O₂=7 ， 则两圆的位置关系为：　　　　　　　　　　　　　　　　 (　　　)

　 A. 相离　　　B. 相交　　C. 内切　　 D. 外切

4. 已知关于x 的不等式 x+a ≤ 2 的解集如图所示，则a 的值为：　　　　　　 (　　　)

　 A.　3　　　　B. 1　　　C.　―1　　　D. ―5　

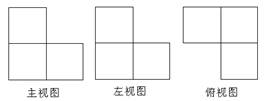5. 如图， 是由几个相同的小正方体搭成的几何体的三视图， 则搭成这个几何体的正方体的个数为：　　　　　　　　　　　　　 (　　　)

　A. 3　　　　 B. 4

　 C. 5　　　　 D. 6

6. 如图，在⊙O中，弦AB的长为4cm ， 圆周角∠C=30⁰ ， 则⊙O的面积为：　　　　　　　　　　　　　　　　　　　　　 (　　　)

　 A. 16π　　　B. 16　　　 C. 4　　　　D. 8π

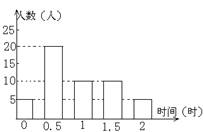7.某学校为了了解初三学生的课外阅读情况，随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，结果见下图， 根据此条形图估计这一天该校学生平均课外阅读时间为：　　　  (　　　)

A. 0.9　 　　 B. 1.15

　 C. 1.25　　　D. 1.5

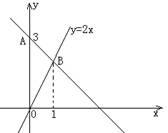8. 如图，过A点的一次函数的图像与正比例函数y=2x的图像相交于点B， 能表示这个一次函数图像的解析式为：　　　　　　　　　　　　　　　　　　　　　　  (　　　)

 A. y=2x+3　　　 B. y=x―3

　 C. y=―x+3　　　D. y=x―

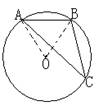
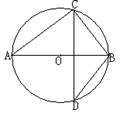9. 如图，已知AB是⊙O的直径，CD是弦且CD⊥AB， BC=6 ， AC=8 ，则sin∠ABD的值为： (　　　)

A. 　　　 B. 　　　C. 　　 D.

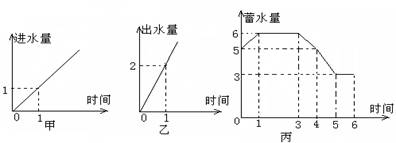10. 水池有2个进水口， 每个进水口进水量与时间的关系如图甲所示， 出水口出水量与时间的关系如图乙所示， 某天0点到6点，该水池的蓄水量与时间的关系如图丙所示，下面的论断中：(1) 0点到1点，打开两个进水口，关闭出水口； (2)1点到3点，同时关闭两个进水口和一个出水口；(3)3点到4点关闭两个进水口， 打开出水口；(4)5点到6点，同时打开两个进水口和一个出水口。　可能正确的有：　　　　 (　　　)

A. 1个　  B. 2个　　

C. 3个　  D. 4个

二. 填空题(本题6小题，每小题5分，共30分)

11. 写一个有一个根为0的一元二次方程__________________；

12. 已知抛物线 y= (x―1)²―4 ， 则顶点坐标为______________；

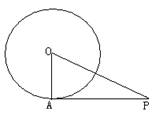
13. 如图，PA是⊙O的切线，切点为A，PA=2，

∠APO=30⁰ ， 则⊙O的半径为_________；

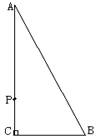
14. 如图 ， Rt△ABC中， ∠C=90⁰ ， BC=5cm ， CA=12cm ， 点P从C出发， 以2cm/秒的速度沿C→A→B方向运动， 若S_△BCp= S_△ABC ，则点P运动的时间为________；

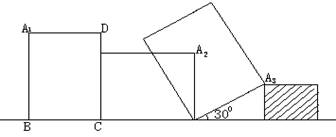15. 如图小明使一长为8cm ， 宽为6cm的长方形木板在桌面上沿顺时针方向做无滑动的翻滚，木板上点A₁在桌面上变化为A₁→A₂→A₃，其中第二次翻滚时被桌面上一小木块挡住，使木板与桌面成30⁰，则点A₁翻滚到A₃位置时，共走过的路径长为_________

16. △ABC中，AB边上的中线CD=3，AB=6，BC+AC=8，则△ABC的面积为______________。

三解答题(本题共8小题，共80分，请务必写出解题过程)

17. (本题8分)先化简：+ 再选一个你喜欢的x的值代入；

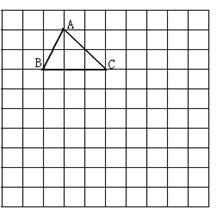
18. (本题8分)如下图在10×10的正方形网格中，每个小正方形的边长均为1个单位，将△ABC向下平移4个单位，得到△A₁B₁C₁ ， 再将△A₁B₁C₁ 绕点C₁ 顺时针旋转90⁰ ， 得到△A₂B₂C₁ 请你画出△A₁B₁C₁ 和△A₂B₂C₁ (不要求写出画法)。

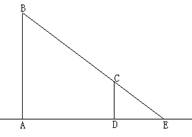
19. (本题8分) 小王从路灯下向前走了5米 ， 发现自己在地面上的影子长DE是2米， 如果小明的身高为1.6米，求路灯的高度AB的值。

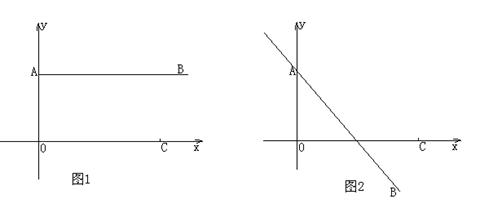
20. (本题8分)为了增强学生的体质，提高学生的素质，省教育厅专门下发文件，要求保证中小学生每天1小时的活动。下面两幅统计图反映了柯城区甲、乙两所中学的学生参加大课间文体活动的情况，请你通过图中的信息回答下面的问题：

(1)通过对图1的分析，写出一条你认为正确的结论；

(2)通过对图2的分析，写出一条你认为正确的结论；

(3)2007年4月甲、乙两所中学参加球类活动的学生共多少人？

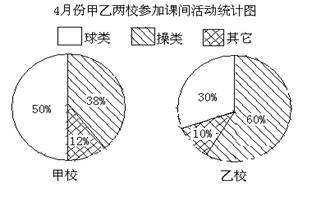
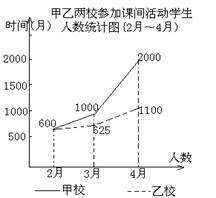
图1　　　　　　　　　　　　　　　　　　　　　  图2

21. (本题10分) 已知正方形ABCD。

(1) 如图1 ， E是AD上一点， 过BE上一点O作BE的垂线 ，交AB于点G ， 交CD于点H ， 求证： BE=GH ；

(2) 如图2 ， 过正方形ABCD内任意一点作两条互相垂直的直线，分别交AD，BC于点E，F，交AB，CD于点G，H，那么EF与GH相等吗?请写出你的结论(不必证明)；

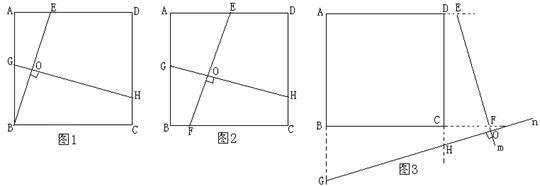(3) 当点O在正方形ABCD的边上或外部时，过点O作两条互相垂直的直线，被正方形相对的两边作它们的延长线截得的两条线段相等吗?其中一种情形如图3， 过正方形ABCD外一点O作互相垂直的两条直线m、n ，直线m与AD、BC的延长线分别交于点E、F ，直线n与AB、DC的延长线分别交于点G、H ， 试就该图对你的结论加以证明。

22. (本题12分)随着居民生活水平的提高，居民对房子的要求也越来越高，带动了房地产行业。2007年衢州市某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于2090万，但不超过2096万，且所筹资金全部用于建房，两种户型的建房成本和售价如下表：

	A	B
成本(万元/套)	25	28
售价(万元/套)	32	36

 

问：(1)该公司对这两种户型住房有哪几种建房方案：

(2)该公司如何建房获得利润最大?

(3)根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元(a>0) ，且所建的两种住房可全部售出，该公司又将如何建房获得利润最大?

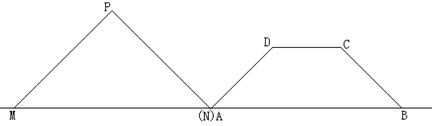
23. (本题12分) 如图，在等腰梯形ABCD中， AB∥DC， ∠A=45⁰ ， AB=15cm ， CD=6cm ， 等腰直角三角形PMN的斜边MN=15cm ，且点A与N点重合 ，MN和AB在一条直线上，设等腰梯形ABCD不动，等腰直角三角形PMN沿AB所在直线以1cm/s 的速度向右移动，直到点N与点B重合为止。

(1)等腰直角三角形PMN在整个移动过程中与等腰梯形ABCD重叠部分的形状由________形变化为________形。

(2)设当等腰直角三角形PMN移动x(s) 时，等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积为y(cm²) ， 求y 与x 的函数表达式 。

(3) 当x =10(s) ，求重叠部分的面积。

24. (本题14分) 在平面直角坐标系中，A点坐标为(0 ， 4 ) ， C点坐标为 (10 ， 0 )。

(1) 如图1：若直线AB∥OC ，直线AB上有一动点 P ( P在第一象限) ，若△POC为等腰三角形时，求P点坐标。

(2) 如图2 ：若直线AB与OC不平行，过点A的直线y= ―x+4 上是否存在点P，使

∠OPC=90⁰ ，若存在这样的点P，求出它的坐标，若不存在，请简要说明理由。

(3)若点P在直线y=kx+4上移动，且只存在唯一一个点P ， 使∠OPC=90⁰ ， 试求出k的值。

初三数学第二学期阶段性质量检测试卷答题卷

一.　选择题（本题共10小题，每小题4分，共40）

题号	1	2	3	4	5	6	7	8	9	10
答案

二. 填空题(每小题5分，共30分)

11. ____________　　　　  12. ____________　　　　  13. ____________

14. ____________　　　　　15. ____________　　　　  16. ____________

三. 解答题(共8题，第17—20题， 每题8分，第21题10分， 第22—23题，每题12分，第24题，14分，共80分)

17. (本题8分)　+ 　　　　　　　　　　　　 18. (本题8分)

19. (本题8分)

20. (本题8分)

(1)　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　

(2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

(3)　　　　　　　　　

21. (本题10分)

22. (本题12分)

23. (本题12分)

24. (本题14分)