初三数学第二学期期初检测（）

一．选择题（本题共10小题，每小题4分，共40分）请选出各题中一个符合题意的正确选项，不选﹑多选﹑错选均不给分。

1．元月份某一天，北京市的最低气温为-6 ⁰C，衢州市的最低气温为2 ⁰C，那么这一天衢州市的气温比北京市的最低气温高（　　 ）

　 A．6 ⁰C　　　　 B．4 ⁰C　　　　　C．-8 ⁰C　 　　　　D．8 ⁰C

2．方程x（x+1）=0的解是（　　 ）

A．x= -1　　　  B． x=0　　　　 C． x₁=0,　x₂=1　　D． x₁=0,　x₂= -1

3. 已知小明同学身高1.5米，经太阳光照射，在地面的影长为2米，若此时测得一塔在同一地面的影长为60米，则塔高应为 (　　 )

A. 90米　　　　　B. 80米　　　　 C. 45米　　　　 D. 40米

4．下列运算正确的是（　　 ）

A．　　　　　　　  B．　

C．D．

5．若0<a<1，则点M(a-1，a)在第(　　 )象限

　  A．第一　　　　　　B．第二　　　　　　C．第三　　 　　 D．第四

6．学校开展为贫困地区捐书活动，以下是八名学生捐书的册数：2，2，2，3，6，5，6，7，则这组数据的中位数为(　　 )

　 A．2　　　　 B．3　　　　　 C．4 　　　　 D．4.5

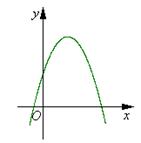
7．二次函数图象的大致位置如图，下列判断

错误的是（　　 ）　　　　　　　　 

A．　B．　C．　D．

8．如图所示，将矩形纸片ABCD沿虚线EF折叠，使点A落在点G上，点D落在点H上；然后再沿虚线GH折叠，使B落在点E上，点C落在点F上；叠完后，剪一个直径在BC上的半圆，再展开，则展开后的图形为（　　 ）

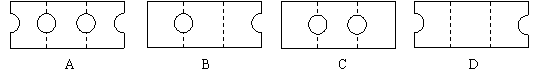9．在等腰△ABC中，∠C=90°，BC=2cm.若以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，则点B′ 与点B的原来位置相距（　　 ）

A. 　　　　　 B.2cm　　　　　  C. 　　　　　D.

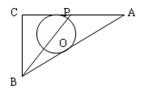10. 如图，在ΔABC中，∠C=90°，AC=8，AB=10，点P由点C出发以每秒2cm的速度沿线段CA向点A运动（不运动到A点）。⊙O的圆心在BP上，且⊙O分别与AB、AC相切，当点P运动2秒时，⊙O的半径是（　　　 ）

A、cm　　 B、cm　　

 C、cm　　 D、2cm

二．填空题（本题共6小题，每小题5分，共30分）

11. 若正比例函数y=mx (m≠0)和反比例函数y= (n≠0)的图象都经过点(2,3)，则m=______，n=_________ .

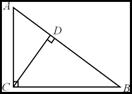
12. 如图，若CD是RtΔABC斜边上的高，AD=3，CD=4，

则BC=__________ .

13. 若非零实数a,b满足4a²+b²=4ab，则=___________.

14. 如果关于x的不等式 (a+1) x>a+1的解集为x<1，那么a的取值范围是______________.

15. 将正面分别标有数字6，7，8，背面花色相同的三张卡片洗匀后，背面朝上放在桌面上．

随机地抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数字，能组成两位数恰好为“68”的概率是_______________。

16.如图是一个正方体的表面展开图，已知正方体相对两个面

上的数值相同，且不相对两个面上的数值不相同，则“★”面

上的数为___________.

三.解答题(本题共8小题,共80分.请务必写出解答过程)

17．（本题满分8分）计算： (3-)⁰-3^-2-+-+3tan30⁰．

18．（本题满分8分）先化简，再求值：，其中。

19．（本题满分8分）已知：如图，BD为平行四边形ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD、BC分别交于点E、F。

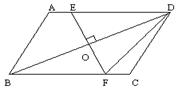求证：DE=DF。

20．（本题满分8分）同学：你去过黄山吗？在黄山的上山路上，有一些断断续续的台阶，如图是其中的甲、乙段台阶路的示意图， 图中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q，(10cm＜a＜b＜c＜d＜e＜f＜g＜h＜20cm,且 p＜q），请你用所学过的有关统计知识（平均数、中位数、方差和极差）回答下列问题：

（1）两段台阶路有哪些相同点和不同点？

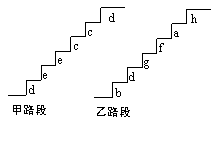（2）哪段台阶路走起来更舒服？为什么？

（3）为方便游客行走，需要重新整修上山的小路.

对于这两段台阶路，在台

阶数不变的情况下，请你

提出合理的整修建议.

21．（本题满分10分）台球是一项高雅的体育运动．其中包含了许多物理学、几何学知识。图①是一个台球桌，目标球F与本球E之间有一个G球阻挡

(1)击球者想通过击打E球先撞击球台的AB边．经过一次反弹后再撞击F球。他应将E球打到AB边上的哪一点?请在图①中作出这一点H．并作出E球的运行路线；(不写画法．保留作图痕迹)

(2)如图②．现以D为原点，建立直角坐标系，记A(O，4)．C(8，0)．E(4，3)，F(7，1)，求E球按(1)中作出的运行路线运行到F球的路线长度．(忽略球的太小)

22．（本题满分12分）某批发市场欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办海产品运输业务，已知运输路程为120千米，汽车和火车的速度分别是

60千米/时、100千米/时，两货运公司的收费项目及收费标准如下表所示：

（注：元/吨·千米表示每吨货物每千米的运费；元/吨·小时表示每吨货物每小时冷藏费）

（1）设批发商待运的海产品有x（吨），汽车货运公司和铁路货运公司所要收取的费用分别为y₁（元）和y₂（元），分别写出y₁、y₂与x的关系式。

（2）若该批发商待运的海产品不少于30吨，为节省运费，他应选哪个货运公司承担运输业务？

23．（本题满分12分）如图，已知Rt△ABC中，∠ABC＝90°，D是AC的中点，⊙O经过A、B、D三点，CB的延长线交⊙O于点E，过点E作⊙O的切线，交AC的延长线于点F．在满足上述条件的情况下，当∠CAB的大小变化时，图形也随着改变，但在这个变化过程中，有些线段总保持着相等的关系．

（1）连结图中已标明字母的某两点，得到一条新线段与线段CE相等，并说明理由；

（2）若CF＝CD，求的值；

（3）若，试用含n的代数式表示．

（直接写出结果）

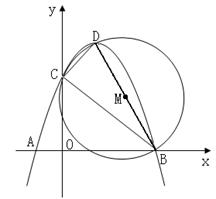
24．（本题满分14分）抛物线y=ax²+bx+c(a<0)交x轴于点A(-1，0)、B(3，0)，交y轴于点C，顶点为D，以BD为直径的⊙M恰好过点C.

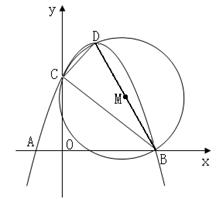(1)求顶点D的坐标(用a的代数式表示)；

(2)求抛物线的解析式；

(3)抛物线上是否存在点P使△PBD为直角三角形?

若存在，求出点P的坐标；若不存在，说明理由.

初三数学第二学期期初检测

一、选择题（本题共10小题，每小题4分，共40分）

题号	1	2	3	4	5	6	7	8	9	10
答案

二、填空题（本题共6小题，每小题5分，共30分）

11．　　　　　　　　　　12．　　　　 　　　　　 13．　　　　　　　　

14．　　　　　　　　　　15．　　　　　　　　　　16．_________________

三、解答题（第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）

17．　　　　　　　　　　　　　　　　 　　　  18．

 

19.

20.　　　　　　　　　　　　　　　　　　　　　

21.

22.

23.

24.