初三数学模拟试卷6

一、选择题（每小题4分，共48分）

1.–3的相反数是…………………………………………………………………………(　　)

A.　　　　　  B.3　　　　　　 C. - 　　　D.-3

2.“天上星星有几颗,7后跟上22个0”这是国际天文学联合会上宣布的消息,用科学记数法表示宇宙空间星星颗数为…………………………………………………………………(　  )

A.700×10²⁰　　　B.7×10²³　　　  C.0.7×10²³　　D.7×10²²

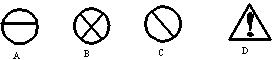
3. 下列几个图形是国际通用的交通标志，其中不是中心对称图形的是……………（　　）

4.粮仓顶部是圆锥形,这个圆锥的底面半径为2m,母线长为3m,为防雨需在仓顶部铺上油毡,这块油毡面积是………………………………………………………………………… (　　 )

A.6m²　　　　　　 B.6πm²　　　　 C.12m²　　　　D.12πm²

5. 下列图中能过说明∠1>∠2的是…………………………………………………… (　　 )

　　　　　　 

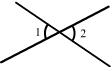
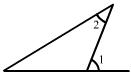
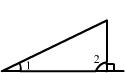
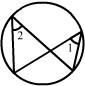
A. 　　　　　　　　　B. 　　　　　　　　 　 C. 　　　　　　　　D.

6. 在一定条件下，若物体运动的路程s（米）与时间t（秒）的关系式为，则

当t=4时，该物体所经过的路程为……………………………………………………（　　）

A．28米　　　　　B．　48米　　　　　C．68米　　　　　D．　88米

7. 已知方程x²－5x＝2－, 用换元法解此方程时，可设y＝,则原方程

化为………………………………………………………………………………………（　　）

 A.y²－y＋2＝0　 B.y²－y－2＝0　 C.y²＋y－2＝0　 D.y²＋y＋2＝0

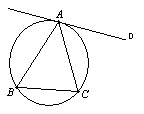
8. 如图，直线AD与△ABC的外接圆相切于点A，

若∠B＝60°，则∠CAD等于………………………………（　　）

A.30°　 B.60°　C.90°　 D.120°

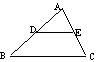9.  如图，△ABC中，D、E分别在AB、AC上，且DE∥BC，若

AE∶EC＝1∶2，AD＝6，则AB的长为………………………（　　）

A.18　 　　 B.12　  　 C.9　　　D.3

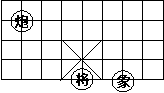 10. 如图，若在象棋盘上建立直角坐标系，使“将”

位于点（1，－2），“象”位于点（3，－2），

则炮位于点………………………………（　　 ）

 A.（1，3）　　B.（－2，1）　

 C.（－1，2）　D.（－2，2）

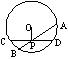11. 如图，已知⊙O的弦AB，CD交于点P，且OP⊥CD，若CD＝4，

则AP•BP的值为……………………………………………………（　　）

 A.2　　 　B.4　　　 C.6　　　D.8　

12.设“●、■、▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，如果要使第三架也平衡，那么“？”处应放“■”的个数为……………………………（　　 ）

A.5　　　　　　　B.4　　 　　　　 C.3　　　　　  D.2

二、填空题（每题5分，共30分）

13.请你写出一个图象经过点（1，1）的函数解析式：　　　　　 .　　　　　　　　　 

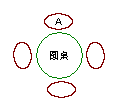
14．一张圆桌旁有四个座位，A先坐在如图所示的座位上，B、C、D三

人随机坐到其他三个座位上。A与B不相邻而坐的概率是　　　.

15.为了合理利用电力资源，缓解用电紧张状况，我市电力部门出台了使用 “峰谷电”的政

策及收费标准（见表），已知王老师家4 月份使用“峰谷电”95千瓦时，缴电费43.40元，问王老师家4月份“峰电”和“谷电”各用了多少千瓦时？设王老师家4月份“峰电”用了x千瓦时，根据题意，列方程得：　　　　　  　　　　　　　.

	用电时间段	收费标准
峰电	08：00—22：00	0．56元/千瓦时
谷电	22：00—08：00	0．28元/千瓦时

16. 因式分解ab-a+b-1＝　　　　　　　　　　　　　　.

17．一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪彩成四个小正方形，如此继续下去，……，

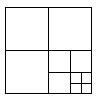根据以上操作方法，请你填写下表：

操作次数n	1	2	3	4	5	…	N
正方形的个数	4	7	10			…

18．如图，如图，时钟的钟面上标有1，2，3,……，12共12个数，一条

直线把钟面分成了两部分.请你再用一条直线分割钟面，使钟面被

分成三个不同的部分且各部分所包含的几个数的和都相等，则其

中的两个部分所包含的几个数分别是　　　 和.　　　　　 .

三、解答题（本题有7小题，共72分）

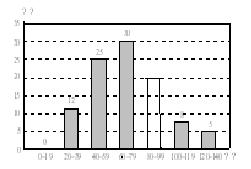
19．（本题8分）计算：

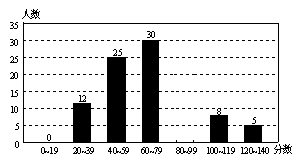20．（本题8分）平阳区初三有100名学生参加了初中数学竞赛．已知竞赛成绩都是整数，试题满分为140分，参赛学生的成绩统计情况如下图：

请根据以上信息完成下列问题：

（1）将该统计图补充完整；

（2）竞赛成绩的人数最多的一组落在上表中的　　 　　　 分数段内；

（3）若80分以上 (含80分)的考生均可获得不同等级的奖励，该校参加竞赛的学生获奖率为　　 %．

21. （本题10分）如图，△ABC中，AC＝BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．

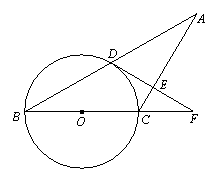求证：（1）AD＝BD；

（2）DF是⊙O的切线．

22．（本题10分）（6分）作图题，如图，把一个正六边形分成6个部分，分别种上6种不同的花草，要求每个部分形状相同，面积也相同，请你设计出两种符合题意的图案（必要时写上说明或标记）

23. （本题12分）已知关于x的方程的两根是一个矩形两邻边的长.⑴k取何值时，方程在两个实数根；⑵当矩形的对角线长为时，求k的值.

24．（本题12分）随着海峡两岸交流日益增强，通过“零关税”进入我市的一种台湾水果，其进货成本是每吨0.5万元，这种水果市场上的销售量（吨）是每吨的销售价（万元）的一次函数，且时，；时，。

（1）求出销售量（吨）与每吨的销售价（万元）之间的函数关系式；

（2）若销售利润为（万元），请写出与之间的函数关系式，并求出销售价为每吨2万元时的销售利润。

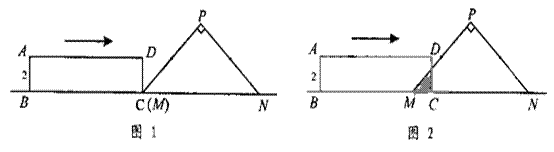
25．(本题满分14分)如图1，Rt△PMN中，∠P＝90°，PM＝PN，MN＝8cm，矩形ABCD的长和宽分别为8cm和2cm，C点和M点重合，BC和MN在一条直线上。令Rt△PMN不动，矩形ABCD沿MN所在直线向右以每秒1cm的速度移动（如图2），直到C点与N点重合为止。设移动x秒后，矩形ABCD与△PMN重叠部分的面积为y。求y与x之间的函数关 系式。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

参考答案：

一、选择题：BDDABD，CBABBA。

二、填空题：13、y=x或y=x²或y=2x-1或等；14、；15、0.56x+0.28(95-x)=43.3

16、(a+1)(b-1)；17、13，16，3n+1（前两空各1分，后一空3分）；18、10，9，4，3和5，6，7，8。

三、解答题：

19、解：原式=16+2-（2+√3）………………………………6^/

　　　　　  =4+-2-=2…………………………………………8^/

20、解

（1）画图2分

（2）60——79；（3）33。（每空3分）

21、证明：

（1）连结CD

∵BC是⊙O的直径　　  ∴BD⊥CD

AC=BC　　　　　　　 ∴AD=BD　 …………………………4^/

（2）连结OC

∵AD=BD，BO=CO　　　　OD是∆ABC的中位线

∴OD∥AC　　 ∵ED⊥CA　　∴OD⊥DF　　 ∴DF是⊙O的切线……………………10^/

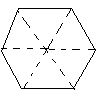
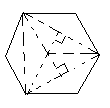22、

　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　  　　　　　 

23. 解(1)∵方程在两个实数根　　　∴△=(k+1)²-4(k²+1)≥0

解得：k≥　　 ∴当k≥时，方程在两个实数根.…………4^/

(2)设方程的两根为x₁,x₂.由韦达定理得:

x₁+x₂=k+1　　 x₁x₂=k²+1　 且x₁²+x₂²=5　　　 ………………6^/

∴(x₁+x₂)²-2x₁x₂=5　　　即　　(k+1)²-2(k²+1)=5

整理得k²+4k-12=0　　 解得k₁=2,k₂=-6

∵k≥　　 ∴k=2　　　　　　　　　　　　  ………………12^/

24. 解：(1)设y关于x的一次函数为y=kx+b

　　由题意得：　　解得：

∴y=-x+3　　　　  …………………………………4^/

(2)由题意得：w=y(x-0.5)=(-x+3)(x-0.5)

即　　w=-x²+3.5x-1.5　……………………………9^/

　　当x=2时，w=1.5　　　……………………………11^/

　 答：当销售价为每吨2万元时的销售利润为1.5万元。………12^/

25.解：

（1）当C点由M点运动到F点的过程中（0≤x≤2），　

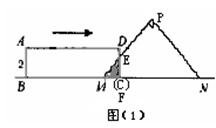如图①所示，设CD与PM交于点E，

则重叠部分图形是Rt△MCE，且MC＝EC＝x，

∴  ≤x≤2)

　

　　　　　　　　　　　　　　 

 

(2)当C点由F点运动到T点的过程中（ 2≤x≤6　），

如图②所示，重叠部分是直角梯形MCDG，

∵MC＝x，MF＝2，∴FC＝DG＝x－2，且DC＝2，

∴  （ 2≤x≤6）　）　　　　　　　　　　　　　　　　　　 

（3）当C点由T点运动到N点的过程中（　6≤x≤8 ），

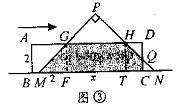如图③所示，设CD与PN交于点Q，

则重叠部分是五边形MCQHG，

∵MC＝x，∴CN＝CQ＝8－x，且DC＝2，

∴

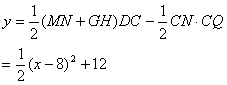
拟试卷双向细目表

题号	题型	分值	知识点	能力要求	难度
1	选择题	4	相反数的的概念	a	Ⅰ
2	选择题	4	科学记数法	a	Ⅰ
3	选择题	4	中心对称图形	a	Ⅰ
4	选择题	4	圆锥的侧面积应用	a	Ⅰ
5	选择题	4	看图比较角的大小	a	Ⅰ
6	选择题	4	求二次函数的值	a	Ⅰ
7	选择题	4	换元法	a	Ⅰ
8	选择题	4	弦切角	a	Ⅰ
9	选择题	4	平行线分线段成比例	a	Ⅰ
10	选择题	4	平面直角坐标系	a	Ⅰ
11	选择题	4	相交弦定理	b	Ⅰ
12	选择题	4	方程组的应用	b	Ⅱ
13	填空题	5	开放题(写出 一个函数解析式)	a	Ⅰ
14	填空题	5	概率应用	a	Ⅰ
15	填空题	5	一元一次方程的应用	b	Ⅰ
16	填空题	5	因式分解	b	Ⅰ
17	填空题	5	探索规律	b	Ⅰ
18	填空题	5	图形分割与有理数的计算	b	Ⅱ
19	解答题	8	实数的运算	a	Ⅰ
20	解答题	8	统计知识应用	a	Ⅰ
21	解答题	8	圆的基本知识及等腰三角形性质	a	Ⅰ
22	画图题	10	因式分解与拼图	b	Ⅱ
23	解答题	12	根的判别式与韦达定理	b	Ⅱ
24	解答题	12	一次函数与二次函数最值的应用	c	Ⅱ
25	解答题	14	动态问题及应用	c	Ⅲ