数学中考模拟试卷 (3)
一、选择题(本题有12小题,每小题4分,共48分。每小题只有一个选项是正确的,不选、多选、错选均不给分。)
1.2的相反数是………………………………………………………( )
A.2 B.-2 C.![]() D.
D.![]()
 2.y=(x-1)2+2的对称轴是直线……………………………………( )
2.y=(x-1)2+2的对称轴是直线……………………………………( )
A.x=-1 B.x=1 C.y=-1 D.y=1
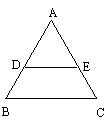
3.如图,DE是ΔABC的中位线,则ΔADE与ΔABC的面积之比是( )
A.1:1 B.1:2 C.1:3 D.1:4
 4.右图是一块手表,早上8时的时针、分针的位置如图所示,那么分针与时针所成的角的度数是( )
4.右图是一块手表,早上8时的时针、分针的位置如图所示,那么分针与时针所成的角的度数是( )
A.60° B.80°
C.120° D.150°
5.函数![]() 中自变量x的取值范围是…………………………( )
中自变量x的取值范围是…………………………( )
A.x≠-1 B.x>-1 C.x≠1 D.x≠0
6.下列计算正确的是…………………………………………………( )
A.a2·a3=a6 B.a3÷a=a3 C.(a2)3=a6 D.(3a2)4=9a4
7.在下列图形中,既是中心对称图形又是轴对称图形的是………( )
A.等腰三角形 B.圆 C.梯形 D.平行四边形
|
A.69 B.54
C.27 D.40
9.相交两圆的公共弦长为16cm,若两圆的半径长分别为10cm和17cm,则这两圆的圆心距为…………………………………………………………( )
A.7cm B.16cm C.21cm D.27cm
10.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车。车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶。下面是行驶路程s(米)关于时间t(分)的函数图像,那么符合这个同学行驶情况的图像大致是…………………………………………………( )
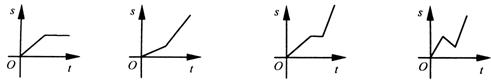 |
A B C D
11.已知方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,k的取值是( )
A.-3或1 B.-3 C.1 D.3
12.某超级市场失窃,大量的商品在夜间被罪犯用汽车运走。三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(1)罪犯不在A、B、C三人之外;(2)C作案时总得有A作从犯;(3)B不会开车。在此案中能肯定的作案对象是( )
A.嫌疑犯A B.嫌疑犯B C.嫌疑犯C D.嫌疑犯A和C
二、填空题(本题有6小题,每小题5分,共30分)
13.写出一个3到4之间的无理数 。
14.分解因式:a3-a= 。
 15.如图,在甲、乙两地之间修一条笔直的公路,
15.如图,在甲、乙两地之间修一条笔直的公路,
从甲地测得公路的走向是北偏东48°。甲、乙两地间
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 同时开工,若干天后,公路准确接通,则乙地所修公
同时开工,若干天后,公路准确接通,则乙地所修公
路的走向是南偏西 度。
16.请写出一个开口向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式 。
17.亮亮想制作一个圆锥模型,这个模型的侧面是用一个半径为9cm,圆心角为240°的扇形铁皮制作的,再用一块圆形铁皮做底。请你帮他计算这块铁皮的半径为 cm。
18.某市民政部门今年元宵节期间举行了“即开式社会福利彩票”销售活动,设置彩票3000万张(每张彩票2元),在这些彩票中,设置了如下的奖次:
| 奖金(万元) | 50 | 15 | 8 | 4 | … |
| 数量(个) | 20 | 20 | 20 | 180 | … |
如果花2元钱购买1张彩票,那么能得到8万元以上(包括8万元)大奖的概率是 。
三、解答题(本题有9小题,共72分)
(在下面的19、20两题中任选做一题,若两题都答,按19题评分。)
19.(本题8分)解方程:![]()
20.(本题8分)![]()
我选答 题。
21.(本题8分)请用“○○、△△、=”(两个圆、两个等腰三角形、两条平行线段)为材料,在所给空白处,设计出一个独特且有意义的图形,并用简练的文字说明你的创意。
我的设计是: 我的创意是:
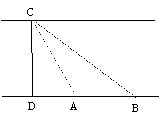
22.(本题8分)下表是明明同学填写实习报告的部分内容:
| 题目 | 在两岸近似平行的河段上测量河宽 |
| 测量目标图示 |
|
| 测得数据 | ∠CAD=60° AB=20米 ∠CBD=45° ∠BDC=90° |
请你根据以上的条件,计算出河宽CD(结果保留根号)。
![]()
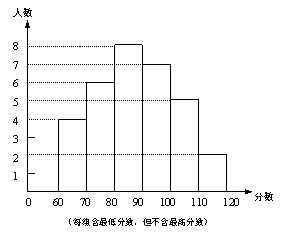 23.(本题10分)某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频率分布直方图。
23.(本题10分)某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频率分布直方图。
请回答:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)图中还提供了其它信息,例如该中学没有获得满分的同学等等。请再写出两条信息。
(在下面的24、25两题中任选做一题。若两题都答,按24题评分。)
24.(本题12分)某校准备在甲、乙两家公司为毕业班学生制作一批纪念册。甲公司提出:每册收材料费5元,另收设计费1500元;乙公司提出:每册收材料费8元,不收设计费。
(1)请写出制作纪念册的册数x与甲公司的收费y1(元)的函数关系式。
(2)请写出制作纪念册的册数x与乙公司的收费y2(元)的函数关系式。
(3)如果学校派你去甲、乙两家公司订做纪念册,你会选择哪家公司?
25.(本题12分)新华文具店的某种毛笔每支售价25元,书法练习本每本售价5元,该文具店为促销制定了两种优惠办法。
甲:买一支毛笔就赠送一本书法练习本;
乙:按购买金额打九折付款。
实验中学欲为校书法兴趣小组购买这种毛笔10支,书法练习本x(x≥10)本。
(1)请写出用甲种优惠办法实际付款金额y甲(元)与x(本)之间的函数关系式;
(2)请写出用乙种优惠办法实际付款金额y乙(元)与x(本)之间的函数关系式;
(3)若购买同样多的书法练习本时,你会选择哪种优惠办法付款更省钱;
我选答 题。
26.(本题12分)某学习小组在探索“各内角相等的圆内接多边形是否为正多边形”时,进行如下讨论:
 甲同学:这种多边形不一定是正多边形,如圆内接矩形;
甲同学:这种多边形不一定是正多边形,如圆内接矩形;
乙同学:我发现边数是6时,它也不一定是正多边形。
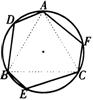
如右图,ΔABC是正三角形,AD=BE=CF,可以证明六边形ADBECF的各内角相等,但它未必是正六边形;
丙同学:我能证明,边数是5时,它是正多边形。我想,边数是7时,它可能也是正多边形。
 ……
……
(1)请你说明乙同学构造的六边形各内角相等。
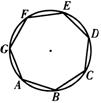
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如右图)是正七边形(不必写已知、求证)。
(3)根据以上探索过程提出你的猜想(不必证明)。

|

|
|
|
![]()
|
|
|
|
|
(3)若(1)的条件不变,当点C在劣弧AD上运动时,应再具备什么条件可使结论BG2=BF·BO成立?试写出你的猜想,并说明理由。
附加题:探究数学“黑洞” (10分)
“黑洞”原指非常奇怪的天体,它体积小,密度大,吸引力强,任何物体到了它那里都别想再“爬”出来。无独有偶,数学中也有类似的“黑洞”,满足条件的所有数,通过一种运算,都能被它“吸”进去,无一能逃脱它的魔掌。譬如:任意找一个3的倍数的数,先把这个数的每个数位上的数字都立方,再相加,得到一个新数,然后把这个新数的每个数位上的数字再立方,再相加,得到一个新数,然后把这个新数的每个数位上的数字再立方,求和,……,重复运算下去,就能得到一个固定的数T= ,我们称它为数字“黑洞”。
你愿意把得到上述结论的探究方法与他人交流吗?若愿意,请在横线上写出这个数并在下方简单写出你的探究过程。(结论正确且所写的过程敏捷合理可另加分。)
数学中考模拟卷(3)参考答案
一、选择题(每题4分,共48分)
1~5题 B B D C A 6~10题 C B D C C 11~12题 C A
二、填空题(每题5分,共30分)
13.π或![]() 等 14.
a(a+1)(a-1) 15.48
等 14.
a(a+1)(a-1) 15.48
16. y=(x-2)2+3等 17.6 18.![]()
三、解答题
19.20任选一题,每题8分
19.解:6-3(x+1)=x2-1 20.解:![]()
x2+3x-4=0 x-2=4-4x+x2
(x+4)(x-1)=0 x2-5x+6=0
x1=-4,x2=1 (x-2)(x-3)=0
经检验x=1是增根,应舍去 x1=2,x2=3
∴原方程的解为x=-4 经检验x=3是增根,应舍去
∴原方程的解为x=2
21.题共8分,设计、创意各4分,合理均可给分。
22.(8分)
解:设CD=x米,则AD=![]() ,DB=x
,DB=x
∵AB=BD-AD
∴20=x-![]()
x=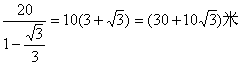
答:河宽CD为(30+10![]() )米。
)米。
23.(1)4+6+8+7+5+2=32人
(2)90分以上人数:7+5+2=14人
![]()
(3)该中学参赛同学的成绩均不低于60分。成绩在80—90分数的人数最多。
24.(1) y1=5x+1500;(2) y2=8x. (3) ∵当y1=y2时,5x+1500=8x, x=500.
当y1>y2时,5x+1500>8x,x<500.
当y1<y2时,5x+1500<8x,x>500.
∴当订做纪念册的册数为500时,选择甲、乙两家公司均可;
当订做纪念册的册数少于500时,选择乙公司;
当订做纪念册的册数大于500时,选择甲公司;
25.(1)y甲=250+5(x-10)=5x+200 (x≥10)
(2)y乙=(250+5x)×90%=4.5x+225 (x≥10)
(3)若y甲=y乙时 x=50
若y甲>y乙时 x>50
若y甲<y乙时 x<50
∴当购买50本书法练习本时,两种优惠办法的实际付款数一样,即可任选一种办法付款;当购买本数在10~50之间时,选择优惠办法甲付款更省钱;当购买本数大于50本时,选择优惠办法乙付款更省钱。
![]()
![]()
![]() 26.(1)由已知得∠AFC对ABC,而AD=CF,
26.(1)由已知得∠AFC对ABC,而AD=CF,
![]()
![]()
![]()
![]()
![]()
![]() 又∵∠DAF对DEF=DBC+CF=AD+DBC=ABC,
又∵∠DAF对DEF=DBC+CF=AD+DBC=ABC,
∴∠AFC=∠DAF
同理可证,其余各角都等于∠AFC.
所以,六边形各内角相等.
![]()
![]() (2) ∵∠A对BDG,∠B对CEA,
(2) ∵∠A对BDG,∠B对CEA,
![]()
![]() 又∵∠A=∠B,∴BEG=CEA.
又∵∠A=∠B,∴BEG=CEA.
![]()
![]() ∴BC=AG.
∴BC=AG.
![]()
![]()
![]()
![]()
![]()
![]()
![]() 同理 AB=CD=EF=AG=BC=DE=FG.
同理 AB=CD=EF=AG=BC=DE=FG.
∴ 七边形ABCDEFG 是正七边形.
(3)猜想:当边数是奇数时(或当边数是3,5,7,9,…时),各内角相等的圆内接多边形是正多边形。
27.(1) 连结OC,证∠OCP=90°即可
(2)∵∠B=30° ∴∠A=∠BGP=60°
∴∠BCP=∠BGP=60°
∴ΔCPG是正三角形.
∴PG=CP=![]()
∵PC切⊙O于C
∴PC2=PD·PE=![]()
又∵BC=![]() ∴AB=6 FD=
∴AB=6 FD=![]() EG=
EG=![]()
∴PD=2![]()
∴PD+PE=![]()
∴以PD、PE为两根的一元二次方程为x2-48x+10![]() =0
=0
(3)当G为BC中点,OG⊥BC,OG∥AC或∠BOG=∠BAC…时,结论BG2=BF·BO成立。要让此结论成立,只要证明ΔBFG∽ΔBGO即可,凡是能使ΔBFG∽ΔBGO的条件都可以。
附加题:
T=153
通过探究总能发现13+53+33=153