九年级数学中考模拟试卷

　　　　　　　　　　

一、选择题（本题有8小题，每题3分，共30分）每小题给出4个答案，其中只有一个是正确的，请把正确选项的字母代号填在答题表一内，否则不给分。

　　　　　　　　 答题表一

题号	1	2	3	4	5	6	7	8	9	10
答案

1.下列算式结果是-3的是　　　　　　　　　　　　　　　　　　  （　 ）

A．(-3)^-1　　 B．(-3)⁰ C．- (-3)　　D． -∣-3∣

2.下列各图经过折叠不能围成一个正方体的是　　　　　　　　　  （　　）

　　　　　　　　　　　　　　　　　　 

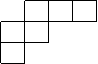
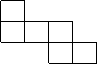
（A）　　　　　　　（B）　　　（C）　　　　　　  （D）

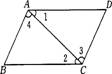3.如图，∠1=∠2，则下列结论一定成立的是　　　　 （　 ）

A．AB∥CD　 B．AD∥BC C．∠B=∠D　　 D．∠3=∠4

4.1nm(纳米)为十亿分之一米，而人体中红细胞的直径约为0.m，那么人体中红细胞直径的纳米数用科学记数法表示为（　　 ）

A．7.7×10³nm　　 B．7.7×10²nm　　C．7.7×10⁴nm　　　D．以上都不对

5.若是y关于x的正比例函数，且y随x的增大而减小，则（　　）

A．k=2　　　　 B．k= - 2　　　C．k=　　　 D．k= -

6.某校计划修建一座既是中心对称图形又是轴对称图形的花坛，从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案，你认为符合条件的是（　）

A． 正三角形　　　  B． 正五边形　　 C． 等腰梯形　　　　D． 菱形

7.为了美化城市，建设中的某休闲中心准备用边长相等的正方形和正八边形两种地砖镶嵌地面，在每一个顶点周围，正方形、正八边形地砖的块数分别是（　）

A. 1、2　　　B. 2、1　　  C. 2、3　　　D.　3、2

8.某校九（3）班的全体同学喜欢的球类运动用图4所示的统计图来表示，下面说法正确的是（　　）

A．从图中可以直接看出喜欢各种球类的具体人数；

B．从图中可以直接看出全班的总人数；

C．从图中可以直接看出全班同学初中三年来喜欢各　　种球类的变化情况；

D．从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系。

9.某机械制造厂制造某种产品，原来每件产品的成本是100元，由于提高生产技术，所以连续两次降低成本，两次降低后的成本是81元。则平均每次降低成本的百分率是　　（　　 ）

A．8.5％　 B. 9％　 C.　9.5％　 D.　10％　

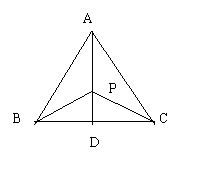
10.如图在△ABC中，AD⊥BC，且D为BC边的中点，

那么以下四个结论中正确的个数是

（1）∠ABP=∠ACP　　　 　（2）AD平分∠BAC　

（3）△ABC是等边三角形 　（4）图中有三对三角形全等

A．1个　　　 B．2个　　　C． 3个　　　　D．4个　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

二.填空题(本题有5小题,每题3分,共15分.请把答案填在下面答题表二内相应的题号下,否则不给分)

　　　　　　　　　　　　　 答题表二

题号	11	12	13	14	15
答案

11.方程的解是_____________.

12.某同学在使用计算器求20个数的时候，错将88误输入为8，那么由此求出的平均数与实际平均数的差为　　　　　　　　　  。

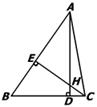
13.如图：△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，

AD、CE交于点H，请你添加一个适当的条件：

　　　　　　　　　　　  ，使△AEH≌△CEB。

14.春节联欢会上，电工师傅在礼堂四周挂了一圈彩灯，其排列规则是：

绿黄黄红红红绿黄黄红红红绿黄黄红红红绿黄黄红红红…

那么，第2006个彩灯是________色的.

15.如图，Rt△ABC中，∠BAC是直角，AB=AC=2，以AB

为直径的圆交BC于D，图中阴影部分的面积为　　　　

三.解答题:(本部分共6题,共55分)

16．（6分）计算:

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

17．（6分）先化简，再求值：

18.（8分）如图,RtΔABC的斜边AB=7,两直角边AC和BC的长是方程

　　 x²-(2k-1)x+4(k-1)=0的两个实数根.　　　　　　　　　　　　  A

求:（1）k的值

（2）RtΔABC的面积

　　　　　　  　　　　　　　　　　　　　B　　　　　　　　　　  C

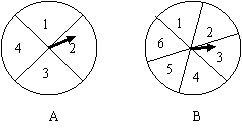
19.（8分）如图，有两个可以自由转动的转盘A、B，转盘A被均匀分成4等份，每份标上数字1、2、3、4四个数字；转盘B被均匀分成6等份，每份标上数字1、2、3、4、5、6六个数字。有人为甲乙两人设计了一个游戏，其规则如下：

（1）　同时转动转盘A与B；

（2）　转盘停止后，指针各指向一个数字（如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止），用所指的两个数字作乘积，如果所得的积是偶数，那么甲得1分；如果所得的积是奇数，那么乙得1分。

你认为这样的规则是否公平？请你说明理由；如果不公平，请你设计一个公平的规则，并说明理由。

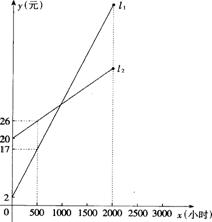
20．（9分）如图，、分别表示一种白炽灯和一种节能灯的费用（费用=

灯的售价+电费，单位：元）与照明时间（小时）的函数图象，假设两种灯的使用寿命都是2000小时，照明效果一样。

（1）根据图象分别求出、的函数关系式；

（2）当照明时间为多少时，两种灯的费用相等？

（3）小亮房间计划照明2500小时，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法（直接给出答案，不必写出解答过程）。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

21.（9分）已知：△ABC中AB=AC，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q.

（1）写出图中与△ABC相似的三角形；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　

（2）试说明：MP＋MQ＝AB；

A

（3）当M位于BC的什么位置时, 四边形AQMP是菱形？在图2中画出图形并予以说明道理。

　

M

C

B

　

 

　　　　 （图1）　　　　（图2）

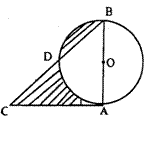
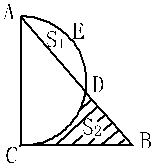22.（9分）如图，以△ABC的边AC为直径的半圆交AB于D，三边长a，b，c能使二次函数的顶点在轴上，且是方程的一个根。

（1）证明：∠ACB=90°；

（2）若设b=2，弓形面积S_弓形AED=S₁，阴影部分面积为S₂，

求（S₂－S₁）与的函数关系式；

（3）在（2）的条件下，当b为何值时，（S₂－S₁）最大？