中考数学模拟卷

　　　　　　　　　　　　 班级　　　　 姓名　　　　  学号　　　　

一、选择题（共12个小题，每小题4分，共48分）

1．以下说法正确的是（　）．

A．4的绝对值是－4　　　　　　　　　　 B．4的倒数是－4

C．4的相反数是　　　　　　　　　　  D．4的平方根是±2

2．2005年1月5日，在中国国家人口计生委7楼的会议厅里，“为印度洋海啸受灾国捐款仪式”简单而又隆重地举行。据悉，这次共筹得捐款共计47万元，用科学记数法表示应记作（　　 ）

　　A．　　　　　　　　　　  B．

　　Ｃ．　　　　　　　　　　　Ｄ．

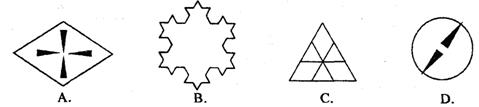
3．下列图形中，不是中心对称图形的是（　）．

４．若两圆的半径分别为3cm和5cm，两圆的圆心距是2cm，则两圆的位置关系是（　  ）

A. 内切　　　　　　　　　B. 外切　　　　　　　　　　C. 相交　　　　 　　D. 内含

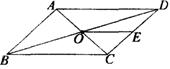
５．如图，平行四边形ABCD中，对角线AC、BD交于点O，OE//BC交CD于点E，若OE=3cm，则AD的长为（  ）．

A．3cm　　　　　　  B．6cm　　　　　　  C．9cm　　　　　　  D．12cm

６．已知x₁、x₂是方程x²－２x－４=0的两根，那么的值是(　　　 )

A．1　　　　 Ｂ．－１　　　　 Ｃ．  ２　　　　　 Ｄ．－２

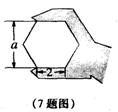
７．如图，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是

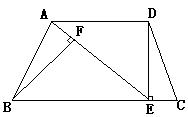
A．　　　　　　　　　　　　　　　B．

C．　　　　　　　　　　　　　　 D．1cm

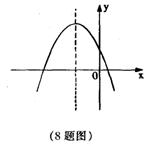
8．已知二次函数的图象如图所示，那么下列判断错误的是

A．a＜0　　　　　　　　　　　　　　　　 B．c＞0

C．　　　　　　　　　　　　 D．ab＜0

　　　　　　　　　　

９．如图，有５为同学正向前方某人用手势示意一个五位数，若站在这５位同学的后面看，这五位数正好是23456,那么他们示意的真实数字是(　　)

　　 　　　　　　　 　　　

　  A.42635　　　　　　 B.45632　　　　　　 C.53624　　　　　　 D.65432

10．小明家喜迁新居，他的父母打算购买同一种形状、同样大小的正多边形瓷砖来贴厨房的墙面．小明特意提醒他父母注意，为了保证贴墙面时既没有缝隙又不重叠，那么，所购买瓷砖的形状不能是（　）．

A．正三角形　　　　 B．正方形　　　　　 C．正六边形　　　　 D．正八边形

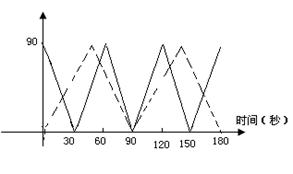
11．一游泳池长９０米，甲乙二人分别在游泳池相对的两边同时朝另一边游，甲的速度是３

米／秒，图中的实线和虚线分别为甲和乙与游泳池一边的距离随游泳时间的变化而变化的图

像，若不计转向时间，则从开始到３分钟止他们相遇的次数为（　　　）　　　　　　　　　　

Ａ．２次　　　　　　Ｂ．３次　　　　　　　Ｃ．４次　　　　　Ｄ．５次

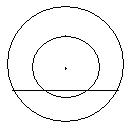
12．两个同心圆Ｏ，半径分别是２和４，大圆的弦ＡＤ交小圆于Ｂ、Ｃ两点且ＡＢ＝ＢＣ＝ＣＤ，如图，则ＡＢ的长等于（　　）

　　Ａ．３　　　　　　　Ｂ．２.５　　　　　　　Ｃ．　　　　　Ｄ．

　

　　　　

二、填空题（共6个小题，每小题5分，共30分）

13．函数中，自变量x的取值范围是________________．

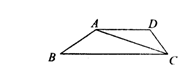14．如图，四边形ABCD中，AD∥BC，如果要使△ABC∽△DCA，

那么还需要补充的一个条件是_______________________．（只要求写

出一个条件即可，不必考虑所有可能的情形）

15． 底面半径2cm，母线长6cm的圆锥，它的侧面展开图的面积是_________________（结果保留） 1６． 湖州某商场为了增加销售额，推出“四月销售大酬宾”活动，其活动内容为：“凡四月份在该商场一次性购物超过50元以上者，超过50元的部分按9折优惠。”在大酬宾活动中，李明到该商场为单位购买单价为40元的办公用品x件（x>2），则应付货款y（元）与商品件数x的函数关系式是________________________________________。　　　　　　　　　　　　　　　　　　 B

17．一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后　　　 A　　　　

经过点B(3,3),则光线从A点到B点经过的路线长是_________．　　　　　

18．电子跳蚤落在数轴上的某点k₀,第一步向左跳1个单位到k₁,　　　　C

第二步由k₁向右跳2个单位到k₂,第三步由k₂向左跳3个单位

到k₃,第四步由k₃向右跳4个单位到k₄,…,按以上规律跳了100步时,电子跳蚤落在数轴上的点k₁₀₀所表示的数恰是19.94,则电子跳蚤的起始位置k₀点所表示的数是_________________．

三、解答题（共8个小题，共72分）

19．(本题8分)计算：

20．(本题8分)如图，田村有一口呈四边形的池塘，在它的四个角Ａ、Ｂ、Ｃ、Ｄ处有一棵大核桃树，田村准备开挖池塘养鱼池，想使池塘的面积扩大一倍，又想保持桃树不动，并要求扩建之后的池塘成平行四边形，请问田村能否实现这一设想？若能，请你设计并画出图形；若不能，请说明理由（画图要保留痕迹，不写画法）．

　　　　　　　Ａ

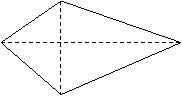
　　 B　　　　　　　　　　  D

　　　　　　　 C

21．(本题8分)如图，等腰梯形ABCD中，AD∥BC，AB＝CD，DE⊥BC于E，AE＝BE，BF⊥AE于F．请你判断线段BF与图中的哪条线段相等．先写出你的猜想，再加以证明．

（1）猜想：BF＝_____________________．

（2）证明：

　　　　　　　　　　　　　　　　　　　　　　　　　　　

22．（本小题满分10分）

某篮球队对运动员进行3分球投篮成绩测试，每人每天投3分球10次，对甲、乙两名队员在五天中进球的个数统计结果如下：

队员	每人每天进球数
甲	10	6	10	8	8
乙	7	9	7	8	9

经过计算，甲进球的平均数为，方差为．

（1）求乙进球的平均数和方差；

（2）现在需要根据以上结果，从甲、乙两名队员中选出一人去参加3分球投篮大赛，你认为应该选哪名队员去？为什么？

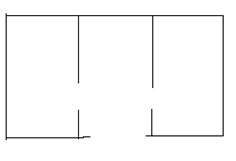
24．(本题12分)用116m长的篱笆为成如图所示的三间鸡舍,门AB的宽为2m,门CD、EF宽1m,问怎样设计鸡舍,才能使它的面积最大.

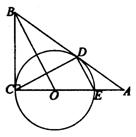
25．(本题12分)已知：如图，中，∠ACB＝90°，点O在  AC上，以O为圆心，OC为半径的圆与AB相切于点D，交AC于点E．

（1）求证：DE∥OB；

（2）求证：；

（3）若⊙O的半径为3，，求AD的长．　　　　　　　　

26.(本小题14分)已知：抛物线与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C．

(1)求A、B、C三点的坐标；

(2)如果直线:y＝x＋b过点A，判断它与双曲线有没有交点，如果有交点，求出交点坐标；如果没有交点，请说明理由；

(3)如果直线y＝t与(2)中的直线l和双曲线分别交于点E、F，直线FD∥y轴，交l于点D．当t的取值变化时，设△CDE的面积为S，写出S与t的函数关系式，并求出自变量t的取值范围．(抛物线的对称轴是与y轴平行的直线，类似的，直线y＝t是与x轴平行的直线．)