初中数学“能力提高”培训题(11)(综合1) 姓名
一、填空题:
1.![]() 的平方根是 ,64的立方根是
。
的平方根是 ,64的立方根是
。
2在![]() ,
,![]() ,—
,—![]()
![]() ,0,12345,2003,
,0,12345,2003,![]() —1这些数中,是无理数的为
—1这些数中,是无理数的为
 3.已知函数y=
3.已知函数y=![]() 的图象经过点(2,—6),则函数y=kx的图象不经过第 象限,函数的图象在每一个象限内从左到右
的图象经过点(2,—6),则函数y=kx的图象不经过第 象限,函数的图象在每一个象限内从左到右
4.在函数y=![]() 中,自变量x的取值范围是
中,自变量x的取值范围是
5在平面直角坐标系中,点P(3,—4)关于y轴的对称点的坐标是
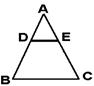
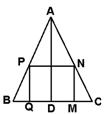
6. 如图,D是AB的中点,DE∥BC,DE交AC于E,DE:BC= , △ADE的面积:梯形DBCE的面积=
 7.如果菱形的两条对角线的长分别是2和2
7.如果菱形的两条对角线的长分别是2和2![]() ,那么它的相邻两个内角的度数分别是
。
,那么它的相邻两个内角的度数分别是
。
8.如图,D为AB上一点,只要具备一个条件: ,就可使△ACD∽△ABC。
9.![]() +
+![]() (x>1)化简的结果是
(x>1)化简的结果是
10、盒字里装有10棵水果糖、2棵奶糖、3颗巧克力糖,随手拿出一棵,恰好是水果糖的机会是 ,恰好是巧克力糖的机会是 。
11.某人购进一批荔枝到市场零售,他卖出的荔枝数量x与售价y的关系如下表:
| 数量x(千克) | 1 | 2 | 3 | 4 | 5 | … |
| 售价y(元) | 3+0.1 | 6+0.1 | 9+0.1 | 12+0.1 | 15+0.1 | … |
则y(元)与x(千克)之间的函数关系式为
二、选择题:
1.下列计算正确的是( )
(A)![]()
![]() =3 (B)
=3 (B)![]() =3 (C)
=3 (C) ![]() =±3 (D)
=±3 (D)![]() =3
=3
2、下列是同类二次根式的是( )
(A)![]() 和
和![]() (B)
(B)![]() 和
和![]() (C)
(C)![]() 和
和![]() (D)
(D)![]() 和
和![]()
3、某人沿坡度i=1:![]() 的桥向上走50米,这时,他离地面的高度是( )米
的桥向上走50米,这时,他离地面的高度是( )米
(A)20 (B)24 (C)25![]() ( D) 25
( D) 25
 4.已知一次函数y=(4—2m)x+(m+1)的图象经过一、三、四象限,则m的取值范围是( )
4.已知一次函数y=(4—2m)x+(m+1)的图象经过一、三、四象限,则m的取值范围是( )
(A) m >—1 (B) m <—1或m >2 (C ) m < 2 ( D) —1 < m < 2
5、在下列函数中,当x (x > 0) 增大时,y反而减小的函数是( )
(A y = ![]() x (B) y= —
x (B) y= —![]() (C)y= 5 x (D)y =
(C)y= 5 x (D)y = ![]()
6.如图,DE∥BC,FE∥AC,下列比例式成立的是
(A)![]() =
= ![]() (B)
(B)![]() =
=![]() (C)
(C)![]() =
=![]() (D)
(D)![]() =
=![]()
 7、如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且cosa=
7、如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且cosa=![]() , AB=4,则 AD的长为( )
, AB=4,则 AD的长为( )
(A)4.5 ( B)5 (C)5.2 (D)6
8、样本101,98,102,100,99的标准差是( )
(A)![]()
![]() (B)0 (C)1 (D)2
(B)0 (C)1 (D)2
9.在△ABC中,AB=24,AC=18,D为 AC上一点,AD=12,在AB上 取一点E,使得以A、D、E为顶点的三角形与△ABC相似,则AE的长应为( )
(A)16 (B)14 (C)16或 14 (D)16或9
10、张老师有4件不同的衬衣和4条不同花色的领带,他要把领带和衬衣搭配,可以有( )种不同的配法
 (A)12 (B)16 (C)8 (D)4
(A)12 (B)16 (C)8 (D)4
三 解答下列各题:
1、
计算:![]() —(
—(![]() —
—![]() ×
×![]() )
)
2、如图,△ABC在平面直角坐标系中:
(1)作△ABC关于y轴的轴对称图形,并写出该图形各顶点的坐标;
(2)以点A为位似中心,将△ABC放大到原来的3倍,并写出新图形各顶点的坐标。
3、小莉有红色、白色、蓝色上衣各一件,黄色、黑色长裤各一条。
(1)用树状图分析小莉穿法的搭配情况;
(2)小莉共有多少种不同的穿法;
(3)小莉上衣穿红色,长裤穿黑色的机会是多少?
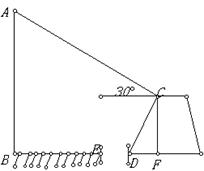
 4、如图
,两建筑物的水平距离BC为24米,从点A测得点D的俯角a=30°,测得点C的俯角
4、如图
,两建筑物的水平距离BC为24米,从点A测得点D的俯角a=30°,测得点C的俯角![]() =60°,求AB和CD两建筑物的高。
=60°,求AB和CD两建筑物的高。
5、若直线![]() 与双曲线
与双曲线![]() 都经过点
都经过点![]() ,且点
,且点![]() 又在直线上。试求直线和双曲线的解析式。
又在直线上。试求直线和双曲线的解析式。
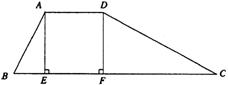 6、为防水患,在漓江上游修筑了防洪堤,其横截面为一梯形(如图所示).堤的上底宽AD和提高DF都是6米,其中∠B=∠CDF.
6、为防水患,在漓江上游修筑了防洪堤,其横截面为一梯形(如图所示).堤的上底宽AD和提高DF都是6米,其中∠B=∠CDF.
(1)求证:△ABE∽△CDF;
(2)如果tanB=2,求堤的下底BC的长.
四、应用题:
1、如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60°方向移动.距台风中心200海里的圆形区域(包括边界)均会受到影响.
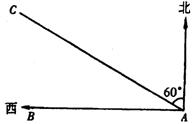 (1)问:B处是否会受到台风的影响?请说明理由.
(1)问:B处是否会受到台风的影响?请说明理由.
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?
2.有一种螃蟹,从海上捕获后不放养最多只能存活两天,如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去,假设放养期内蟹的个体重量基本保持不变.现有一经销商,按市场价收购了这种活蟹1000千克放养在塘内,此时市场价为每千克30元.据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需各种费用支出400元,且平均每天还有10千克蟹死去,假定死蟹均于当天售出,售价都是每千克20元.
(1)设x天后每千克活蟹的市场价为P元,写出P关于x的函数关系式;
(2)如果放养x天后将活蟹一次性出售,并记1000千克蟹的销售总额为Q元,写Q出关于x的函数关系式;
初中数学“能力提高”培训题(12)(综合2) 姓名
一、填空题:
1、(—3)2的算术平方根为 ,—64的立方根为 。
2、化简:![]() = ,
= , ![]() =
。
=
。
3、已知两个相似三角形的面积比为9:4,则它们的相似比为 ,其中一个周长为36,则另一个为 。
4、函数![]() 的自变量
的自变量![]() 的取值范围是 。
的取值范围是 。
5、如图,若∠1=∠2=∠B,则此图中有 组相似三角形,分别是 。
6、如图,已知AD是Rt△ABC 斜边BC上的高,且AB=6,,BC=10,则AC= ,sinα=

7、如图,△ABC中,DE∥BC,已知![]() 则
则![]() ,S⊿ADE:S四边形DBCE=
,S⊿ADE:S四边形DBCE=
8、tan50°×tanα=1,则α= , 4sin260°=
9、一断公路路面,坡度i=1:3,这段路面长100米,那么公路升高 米。
10、边长为2的等边三角形的面积是
11、直线y=-x+m与直线y=4x—1交于x轴上一点,则m=
12、如图,小正方形的边长是1,把图形剪开重新拼成最大的正方形后,正方形的边长是
13、如图,在平行四边形ABCD中,AE=ED,则S△ACE:S△BFC=
14、五个数1,2,4,5,a的平均数是3,则a= ,这五个数的方差是 .
15、 某市出租车计费标准如下:行程不超过3千米收费8元,超过3千米的部分按每千米1.60元计费,车费y和行使路程x之间的函数关系式是
二 选择题(每题3分,共30分)
1、下列各式中,最简二次根式是( )
A)![]() B)
B)![]() C)
C)![]() D)
D)![]()
2、下列各式的计算中,成立的是( )
A)2+![]() =2
=2![]() B)4
B)4![]() —3
—3![]() =1 C)
=1 C)![]() =x+y
D
=x+y
D![]()
 3、根据下列条件,能判断 △ABC∽△DEF的是( )
3、根据下列条件,能判断 △ABC∽△DEF的是( )
A)∠A=52°,∠B=58°;∠E=58°,∠F=80°
B)∠C=102°,∠E=102°,![]() =
=![]()
C)AB=1,AC=1.5,BC=2;EF=8,DE=10,FD=16
D)∠C=∠F=Rt∠ ,AC=5, BC=13, DF=10, EF=26.
4、如果点P(2m+1,—2)在第四象限内,那么的取值范围是( )
A) m > —![]() B) m ≥—
B) m ≥—![]() C) m <—
C) m <—
![]() D) m ≤ —
D) m ≤ —![]()
5、下列函数中,在全体实数范围内,y随x的增大而增大的是( )
A)y=2x2 B)y= —![]() C)y=-2x D)y= -2+x
C)y=-2x D)y= -2+x
6、一多边形面积扩大到原来的2倍,且与原多边形相似,则其周长是原来的( )倍
A)2
B)![]() C)4
D)
C)4
D)![]()
7、“早穿皮袄午穿纱”是对一天中温度的最佳写照,它的含义是一天中的( )
A)最高气温 B)最低温度 C)平均温度 D)温度极差
8、在Rt△ABC中,∠C=90°,下列式子不一定成立的是( )
A) tanA=cot B B) tanA ×cotB=1 C)sin2 A + cos2A = 1 D) sin2A + sin2B = 1
9、1口袋中有一个红球和2个白球,搅匀后从中摸出第一个球,然后放回口袋,搅匀后摸出第二个球,两次摸的球都是红球的机会是( )
A) ![]() B)
B) ![]() C)
C) ![]() D)
D) ![]()
三 解答题:
1、计算:![]() +
+![]() —4
—4![]() (4分)
(4分)
2、在Rt△ABC中,∠C=Rt∠,c=4![]() ,b=2
,b=2![]() ,求边a,及∠A、∠B。
,求边a,及∠A、∠B。
3、某班全体同学在“献爱心”活动中都捐了图书,捐书的情况如下表:
| 每人捐书的册数 | 5 | 10 | 15 | 20 |
| 相应的捐书人数 | 17 | 22 | 4 | 2 |
根据题目中所给的条件回答下列问题:(1)该班的学生共____________名;
(2)全班一共捐了___________册图书;
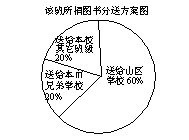 (3)若该班所捐图书拟按右图所示比例分送给山区学校,本市兄弟学校和本校其它班级,则送给山区学校的书比送给本市兄弟学校的书多________册。
(3)若该班所捐图书拟按右图所示比例分送给山区学校,本市兄弟学校和本校其它班级,则送给山区学校的书比送给本市兄弟学校的书多________册。
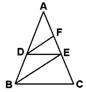
 4、如图,已知∠1=∠2=∠3,则△ABC与△ADE相似吗?为什么?
4、如图,已知∠1=∠2=∠3,则△ABC与△ADE相似吗?为什么?
 5、如图,一个正比例函数的图像和一个一次函数的图像交于点 A(—1,2),且△ABO的面积为5,求这两个函数的解析式。
5、如图,一个正比例函数的图像和一个一次函数的图像交于点 A(—1,2),且△ABO的面积为5,求这两个函数的解析式。
6、城市规划期间,欲拆除一电线杆AB(如图)已知距电线杆AB水平距离14米的D处有一大坝,背水坡CD的坡度i=2:1,坝高CF为2米.在坝顶C处测得杆顶A的仰角为30,D、E之间是宽为2米的人行道.试问:在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由(在地面上,以点B为圆心、以AB为半径的圆形区域为危险区域)
|
|
.
7、辽南素以“苹果之乡”著称,某乡组织20辆汽车装运三种苹果42吨到外地销售。按规定每辆车只装同一种苹果,且必须装满,每种苹果不少于2车。
(1)设用![]() 辆车装运A种苹果,用
辆车装运A种苹果,用![]() 辆车装运B种苹果,根据下表提供的信息求
辆车装运B种苹果,根据下表提供的信息求![]() 与
与![]() 之间的函数关系式,并求
之间的函数关系式,并求![]() 的取值范围;
的取值范围;
(2)设此次外销活动的利润为W(百元),求W与![]() 的函数关系式以及最大利润,并安排相应的车辆分配方案。
的函数关系式以及最大利润,并安排相应的车辆分配方案。
| 苹果品种 | A | B | C |
| 每辆汽车运载量 (吨) | 2.2 | 2.1 | 2 |
| 每吨苹果获利 (百元) | 6 | 8 | 5 |
初中数学“能力提高”培训题(13)(综合3) 姓名
一、填空题
1、若m2的算术平方根是2,则m=________ ;
2、若|-a+5b+1|+![]() =0,则a=________,b=________
=0,则a=________,b=________
3、梯形的上底长为8cm,下底长为10cm,则中位线长为________;
4、同一时刻,一竿的高为2.5米,影长为1米,某旗杆的影长为6米,则旗杆的高为________。
5、已知![]() =2.429,则
=2.429,则![]() =________;若a-
=________;若a-![]() =1,则a+
=1,则a+![]() ________
________
6、已知菱形的两条对角线的比为1∶2,它的周长为8![]() 厘米,则它的两条对角线的长分别为________。
厘米,则它的两条对角线的长分别为________。
7、等腰梯形的上底、下底、腰长分别为4厘米、10厘米、5厘米,则它的高为________。
二、选择题
1、下列各式计算中,正确的是( )
A.(-![]() )2=-7 B.
)2=-7 B.![]() =-0.7 C.-
=-0.7 C.-![]() =0.8 D.(-
=0.8 D.(-![]() )2=0.8
)2=0.8
2、一个多边形的外角和是它内角和的![]() 倍,则这个多边形是( )
倍,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
3、矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线平分一组对角 C.对角线互相平分 D.对角线互相垂直
|
|
|
|
4、如图,△ABC中,DE∥BC,AD=2,DB=3,BC=15,则DE=( )
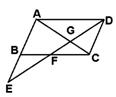
5、.如下图,在平形四边形ABCD中,E是AB延长线
上一点,连结DE交AC于G,交BC于F,那么图中相似
三角形(不包括全等三角形)共有( )
A.6对 B.5对 C.4对 D.3对
6、已知在Rt△ABC中,∠C=90°,CD⊥AB,AC=2厘米;CD=1厘米,则AD的长为( )
A.1厘米 B.![]() 厘米 C.
厘米 C.![]() 厘米 D.28厘米
厘米 D.28厘米
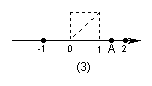 7、如图,所示,以数轴的单位长度为边长作一个正方形,以数轴的原点为圆心、正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是 ( )
7、如图,所示,以数轴的单位长度为边长作一个正方形,以数轴的原点为圆心、正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是 ( )
A.![]() ; B.1.4; C.
; B.1.4; C.![]() ; D.
; D.![]() .
.
三、解答题
1、计算 ①![]() +
+![]() -5
-5![]() +
+![]() -
-![]()
②(3![]() +
+![]() )(
)(![]() -2
-2![]() )-(
)-(![]() -
-![]() )2
)2
2. 在矩形ABCD中,对角线AC=4cm,∠BAC=60°,求矩形的周长和面积
3、如图,△ABC中,D是AB上一点AD∶DB=3∶2。DE∥BC,DF∥BE,AF=9,求EC的长。
|
|
|
|
4、如图,有一块三角形余料ABC,它的边BC=12cm,高AD=8cm,要把它加工成正方形零件PQMN,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,加工成正方形零件的边长PN是多少?
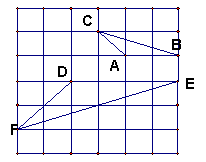 5、如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比。
5、如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比。