2005年绍兴市中考数学试题

总分150分

一．选择题（本大题有12小题，满分48分）下面每题给出的四个选项中只有一个选项是正确的

1．学校篮球场的长是28米，宽是（　　　　）

（A）5米　　　　　（B）15米　　　　　　（C）　28米　　　　　　（D）34米

2．反比例函数的图象在（　　　　　）

（A）第一、三象限　（B）第二、四象限　　（C）第一、二象限　　（D）第三、四象限

3．下列各式中运算不正确的是（　　　　　　）

（A）　　　　　　　（B）　　　　　

（C）　　　　　　　（D）

4．已知圆柱的侧面积为10，则它的轴截面面积为（　　　　　）

（A）　5　　　　（B）　10　　　　　（C）　12　　　　　　（D）　　20

5．“数轴上的点并不都表示有理数，如图中数轴上的点P所表示的数是”，这种说明问题的方式体现的数学思想方法叫做（　　　）

（A）代入法　　　　（B）换元法　　　　　（C）数形结合　　　　　（D）分类讨论

6．实验表明，人体内某种细胞的形状可近似地看作球，它的直径约为0.m，则这个数用科学记数法表示是（　　　　　　）

（A）　　　　（B）　　　（C）　　　　（D）

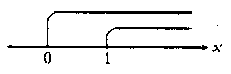
7．不等式组中的两个不等式的解在数轴上表示不如图所示，则此不等式组可以是（　　　）

（A）　　　（B）　　　　（C）　　　　　（D）

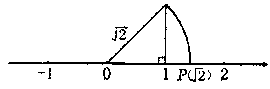
8．将一张正方形纸片，沿图的虚线对折，得图，然后剪去一个角，展开铺平后的图形如右图所示，则图中沿虚线的剪法是（　　　　　　）

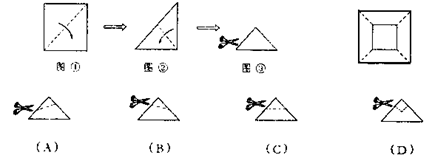
9．化简得

（A）　2　　　　（B）　　　　　　（C）－2　　　　　　　（D）

10．钟老师出示了小黑板上的题目（如图）后，小敏回答：“方程有一根为1”，小聪回答：“方程有一根为2”。则你认为（　　　　　）

（A）只有小敏回答正确　　　　　（B）只有小聪回答正确　　　　　　

（C）小敏、小聪回答都正确　　　（D）小敏、小聪回答都不正确

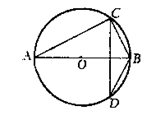
11．如图，已知AB是⊙O的直径，CD是弦且CD⊥AB，BC＝6，AC＝8，则sin∠ABD的值是（　　　）

（A）　　　　　（B）　　　　　　（C）　　　　　　　（D）

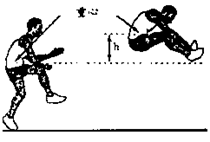
12．小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数（t的单位：s，h的单位：m）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（　　　）

（A）0.71s　　　　　（B）　0.70s　　　　　（C）0.63s　　　　　　（D）0.36s　

　　　

　　

二．填空题（本大题有6小题，满分30分）将答案直接填在各填横线上

13．在等式的两个方格内分别填入一个数，使这两个数是互为相反数且等式成立。则第一个方格内的数是___________

14．在中考体育达标跳绳项目测试中，1分钟跳160次为达标，小敏记录了他预测时1分钟跳的次数分别为145,155,140,162,164，则他在该次预测中达标的概率是__________

15．平移抛物线，使它经过原点，写出平移后抛物线的一个解析式____________________

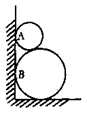
16．如图，两圆轮叠靠在墙边，已知两轮半径分别为4和1，则它们与墙的切点A，B间的距离为________________________

17．实验中学初三年级12个班中共有团圆a人，则表示的实际意义是________________________________

18．（以下两小题选做一题，第（1）小题满分5分，第（2）小题满分为3分。若两小题都做，以第（1）小题计分）

选做第________小题，答案为________

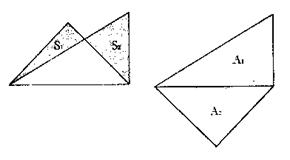
（1）　　　 将一副三角板如图叠放，则左右阴影部分面积:之比等于________

（2）　　　 将一副三角板如图放置，则上下两块三角板面积:之比等于________

三．解答题（本大题有7题，满分72分）以下各题都必须写出解答过程

19．（本题满分8分）

求下列和数的和

20．（本题满分8分）

已知，小敏、小聪两人在的条件下分别计算了P和Q的值，小敏说P的值比Q大，小聪说Q的值比P大，请你判断谁的结论正确，并说明理由。

21．（本题满分10分）

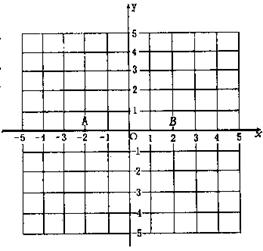
如图，在平面直角坐标系中，已知点为A（－2,0），B（2,0）

（1）　　　 画出等腰三角形ABC（画出一个即可）

（2）　　　 写出（1）中画出的ABC的顶点C的坐标

22．（本题满分10分）

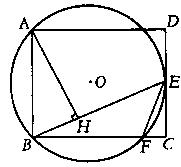
如图矩形ABCD中，过A，B两点的⊙O切CD于E，交BC于F，AH⊥BE于H，连结EF。

（1）　　　 求证：∠CEF＝∠BAH

（2）　　　 若BC＝2CE＝6，求BF的长。

23．（本题满分10分）

班委会决定，由小敏、小聪两人负责选购圆珠笔、钢笔共22支，送给结对的山区学校的同学，他们去了商场，看到圆珠笔每支5元，钢笔每支6元。

（1）　　　 若他们购买圆珠笔、钢笔刚好用去120元，问圆珠笔、钢笔各买了多少支？

（2）　　　 若购圆珠笔可9折优惠，钢笔可8折优惠，在所需费用不超过100元的前提下，请你写出一种选购方案。

24．（本题满分12分）

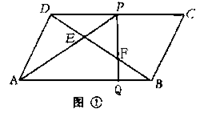
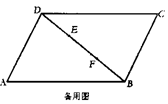
E、F为ABCD的对角线DB上三等分点，连AE并延长交DC于P，连PF并延长交AB于Q，如图①

（1）　　　 在备用图中，画出满足上述条件的图形，记为图②，试用刻度尺在图①、②中量得AQ、BQ的长度，估计AQ、BQ间的关系，并填入下表

长度单位：cm

　　　　

	AQ长度	BQ长度	AQ、BQ间的关系
图①中
图②中

　由上表可猜测AQ、BQ间的关系是__________________

（2）　　　 上述（1）中的猜测AQ、BQ间的关系成立吗？为什么？

（3）　　　 若将ABCD改为梯形（AB∥CD）其他条件不变，此时（1）中猜测AQ、BQ间的关系是否成立？（不必说明理由）

25．（以下两小题选做一题，第（1）小题满分14分，第（2）小题满分为10分。若两小题都做，以第（1）小题计分）

选做第________小题.

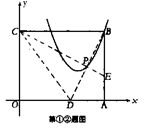
（1）　　　 一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA＝5，OC＝4。

①　如图，将纸片沿CE对折，点B落在x轴上的点D处，求点D的坐标；

②　在①中，设BD与CE的交点为P，若点P，B在抛物线上，求b，c的值；

③　若将纸片沿直线l对折，点B落在坐标轴上的点F处，l与BF的交点为Q，若点Q在②的抛物线上，求l 的解析式。

（2）　　　 一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA＝5，OC＝4。

①求直线AC的解析式；

②若M为AC与BO的交点，点M在抛物线上，求k的值；

③将纸片沿CE对折，点B落在x轴上的点D处，试判断点D是否在②的抛物线上，并说明理由。

参考答案

一．选择题

1．B　　　　2．A　　　　3．C　　　　4．B　　　　5．C　　　　6．C　　　　7．A　　　　8．C　　　　9．A　　　　10．C　　　　11．D　　　　12．D