专题一 实际应用性问题
实际应用性问题是指有实际背景或实际意义的数学问题。这些问题充分体现了贴近学生生活、关注社会热点、形式多样等特点,注重考查学生思维的灵活性和深刻性,要求解题者具有较丰富的生活常识和较强的阅读能力以及数学建模能力。
实际应用性问题涉及的背景有商品买卖、存款和贷款,最优方案、行程问题、交通运输、图案设计、农业生产和生物繁殖等。
实际应用性问题在各地的试卷中成为必考内容,体现了素质教育的要求和新课程标准的理念,由于它们来自生活和生产实践,所以参考条件较多,思维也有一定的深度,解答方法灵活多样。
【典型例题】
例1. 某饮料厂为了开发新的产品,用A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料共50千克,下表是实验的相关数据:
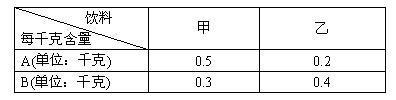
(1)假设甲种饮料需配制x千克。
请你写出满足题意的不等式组,并求出其解。
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元。这两种饮料的成本总额为y元,请写出y与x的函数表达式。并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种的成本总额最低。
分析:根据表格的信息和其他已知条件知甲种原料用量不大于19千克,乙种原料用量不大于17.2千克,可得出(1)的不等式组。
(2)由“成本总额=甲种饮料成本+乙种饮料成本”这个关系式,可列出函数表达式。再运用函数的性质,可确定最低总成本。
解:(1)由条件得
![]()
![]()
(2)依题意得
![]()
由一次函数性质知:k=1>0,y随x的增大而增大。
∴当x=28时,甲、乙两种饮料的成本总额最少。
即y=28+150=178(元)。
例2. 高为12.6米的教学楼ED前有一棵大树AB(如图甲)。
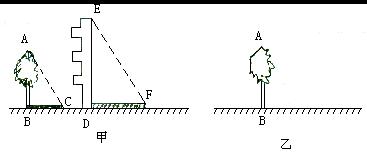
(1)某一时刻测得大树AB,教学楼ED在阳光下的投影长分别是BC=2.4米,DF=7.2米,求大树AB的高度。
(2)用皮尺、高为h米的测角仪,请你设计另一种测量大树AB高度的方案。要求:
a. 在图乙上画出你设计的测量方案示意图,并将应测数据标记在图上。(长度用字母m、n…表示,角度用希腊字母α、β…表示)
b. 根据你所画的示意图和标注的数据,计算大树AB高度。(用字母表示)
分析:(1)可用同一时刻物高与影长成正比获得大树高度。
(2)中的设计方案,要求同学们能根据平时的学习体验及解直角三角形的有关知识获得测量大树的方案。注意的是不要忽视了测角仪的高度。
解:(1)连AC、EF
∵太阳光线是平行线,∴AC∥EF
∴∠ACB=∠EFD
∵∠ABC=∠EDF=90°
∴△ABC∽△EDF
![]()
![]()
∴AB=4.2
答:大树AB的高是4.2米。
(2)如图
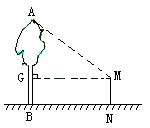
已知测角仪高度为h米,用皮尺可测得测角仪离树距离为m米,用测角仪测得树顶仰角为α,
即BN=GM=m
在Rt△AMG中,AG=m·tanα
∴AB=(m·tanα+h)米
例3. 甲、乙两同学开展“投球进筐”比赛,双方约定:①比赛分6局进行,每局在指定区域内将球投向筐中,只要投进一次后该局便结束。
②若一次未进可再投第二次,以此类推,但每局最多只能投8次,若8次投球都未进,该局也结束;
③计分规则如下:a. 得分为正数或0;b. 若8次都未投进,该局得分为0;c. 投球:次数越多,得分越低;d. 6局比赛的总分高者获胜。
(1)设某局比赛第n(n=1,2,3,4,5,6,7,8)次将球投进,请你按上述约定,用公式、表格或语言叙述等方式,为甲、乙两位同学制定一个把n换算为得分M的计分方案。
(2)若两人6局比赛的投球情况如下。(其中的数字表示该局比赛进球时的投球次数,“×”表示该局比赛8次投球都未进)。
第一局 第二局 第三局 第四局 第五局 第六局
甲 5 × 4 8 1 3
乙 8 2 4 2 6 ×
根据上述计分规则和你制定的计分方案,确定两人谁在这次比赛中获胜。
分析:将实际问题中的计分与投球次数之间进行量化的设计方案,只要满足计分规则的要求即可。
因而可获得不同方案。
解:(1)方案一,如下表:
n(次) 1 2 3 4 5 6 7 8
M(分) 8 7 6 5 4 3 2 1
(未进球计0分),显然上述方案符合计分规则要求。
方案二:
将球投进筐的次数n(次)与得分M(分)之间用关系式
![]()
显然这一计分方案也符合计分规则的要求。
(2)由方案一:可算得甲的得分为:4+0+5+1+8+6=24(分)
乙的得分为:1+7+5+7+3=23(分)
由此可知,在这次比赛中甲获胜。
由方案二:
甲的每局得分分别为:24分、0分、30分、15分、120分、40分;
乙的每局得分分别为:15分、60分、30分、60分、20分、0分。
∴甲的总得分为229分;乙的总得分为185分。
由此知:甲在这次比赛中获胜。
例4. 光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A、B两地区收割小麦;其中30台派往A地区,20台派往B地区。
两地区与该农机租赁公司商定的每天的租赁价格见下表:
每台甲型收割机的租金 每台乙型收割机的租金
A地区 1800元 1600元
B地区 1600元 1200元
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式。并写出x的取值范围。
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案设计出来。
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提出一条合理的建议。
分析:在(1)中,由派往A地乙型收割机为x台。能够正确地用代数式表示往A地的甲型收割机,派往B地的甲、乙型收割机是问题的关键。根据条件可得相应的租赁费用和调运方案。
解:(1)若派往A地区的乙型收割机为x台。
则派往A地区的甲型收割机为(30-x)台
派往B地区的乙型收割机为(30-x)台
派往B地区的甲型收割机为[20-(30-x)]=(x-10)台
∴y=1600x+1800(30-x)+1200(30-x)+1600(x-10)
=200x+74000。

![]()
即x的取值范围是:10≤x≤30(x是正整数)
(2)由题意得:200x+74000≥79600
解得:x≥28
由于10≤x≤30
∴x取28、29、30这三个值。
∴有3种不同分配方案。
①当x=28时,即派往A地区甲型收割机2台,乙型收割机28台,派往B地区甲型收割机18台,乙型收割机2台。
②当x=29时,即派往A地区甲型收割机1台,乙型收割机29台,派往B地区甲型收割机19台,乙型收割机1台。
③当x=30时,即30台乙型收割机全部派往A地区;
20台甲型收割机全部派往B地区。
(3)由于一次函数y=200x+74000的性质知:y随着x的增大而增大。
∴当x=30时,y取得最大值。
如果要使农机租赁公司这50台联合收割机每天获得租金最高,
只需x=30,此时y=6000+74000=80000。
建议农机租赁公司将30台乙型收割机全部派往A地区,20台甲型收割机全部派往B地区,可使公司获得的租金最高。
例5. 如图(1),一个无盖的正方体盒子的棱长为10cm,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙,(盒壁厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,如图(1),在盒子的内部我们先取棱BB1的中点E,再连结AE、EC1,昆虫乙如果沿路径A→E→C1爬行,那么可以在最短的时间内捕捉到昆虫甲,仔细体会其中的道理,并在图(1)中画出另一条路径,使昆虫乙从顶点A沿这条路径爬行,同样可以在最短的时间内捕捉到昆虫甲。(请简要说明画法)。
(2)如图(2)假设昆虫甲从顶点C1以1cm/s的速度在盒子的内部沿棱C1C向下爬行。同时昆虫乙从顶点A以2cm/s的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1s)。
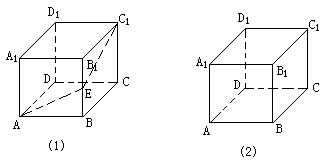
分析:本题难点是两个点是动点,且昆虫乙的路径不惟一,因而确定昆虫乙的几种可能路径是关键;这就必须了解正方体的平面展开图。
在(1)中,类似地在DD1、CD、A1B1、A1D1或BC的中点与A,C1连结的线段上找到由A→C1的最短路径;在(2)中可利用直角三角形的知识获得结论。
解:(1)略。
(2)由(1)知:当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四种路径中的任意一种爬行。可以看出,图(3)、(4)的路径相等,图(5)、(6)的路径相等。
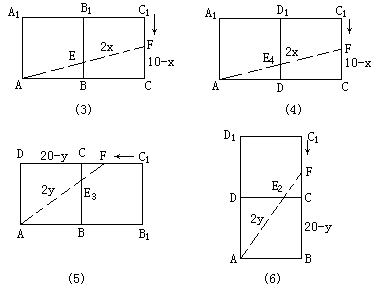
①设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行捕捉到昆虫甲需x秒钟。
由图(3)在Rt△ACF中
![]()
解得x=10
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E3→F爬行捕捉昆虫甲需y秒钟。
由图(5),在Rt△ADF中
![]()
解得y≈8
∴昆虫乙从顶点A爬行捕捉昆虫甲至少需8s。
数学应用与实践包含实际问题中的方案设计问题以及依据数学特征进行的活动,操作和用数学知识解决实际问题等,解这类问题时应注重于对生活中的实际问题进行恰当的分析,从中能够找出与之相关的数学模型,并借助数学知识予以解决,其中所涉及的分类讨论思想、实际问题模型化的思想以及转化的思想方法十分重要,是解决这类问题的关键。
【模拟试题】(答题时间:45分钟)
一、填空。
1. 一商店把某件商品按九折出售仍可获得20%的利润率,若该商品的进价是每价30元,则该件商品的标价是_____________。
2. 小明家粉刷房间,雇了5个工人,干了10天完成,用去涂料费为4800元,粉刷的面积为150m2,最后结算工钱时,有以下三种方案:
(1)按工算,每人每天工资30元;
(2)按涂料费用算,涂料费用的30%作为工钱。
(3)按粉面积算,每平方米付工钱12元。
请你帮小明家出主意,选择方案_____________付钱最合算。
3. 某公司今年5月份的纯利是a万元,如果每个月纯利润的增长率都是x,那么预计7月份的纯利润将达到_____________万元。
4. 有一旅客携带了30kg行李从南京国际机场乘飞机去天津,按民航规定,旅客最多可免费携带20kg行李,超过部分每公斤按飞机票价的1.5%购买行李票,现该旅客购买了120元的行李票,则他的飞机票价格应是_____________。
5. 某兴趣小组决定去市场购买A、B、C三种仪器,其单价分别为3元,5元,7元,购买这批仪器需花费62元,后经过讨价还价,最后以每种各下降1元成交,结果只花了50元就买下了这批仪器,那么A种仪器最多可买_____________件。
6. 某市近年来经济发展迅速,据统计,该市国内生产总值1990年为8.6亿元,1995年为10.4亿元,2000年为12.9亿元,经论证,上述数据适合一个二次函数关系,请你根据这个函数关系,预测2005年该市国内生产总值将达到_____________亿元。
7. 如图1,某公园入口原有三级台阶,每级台阶高为20cm,宽为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C,现在斜坡的坡度∠BCA设计为12°,求AC的长度为_____________。
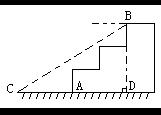
图1
8. 居民楼的采光是人们关心的一个重要问题,冬至是一年中太阳光与地面所成夹角最小的时期,此时只要太阳光在如图2,两楼之间不互相挡住阳光,则一年四季均不为互相挡住阳光了,设此时太阳光与地面的夹角为30°,两楼高均为30米,问两楼之间的水平距离L至少为_____________米时两楼之间才能不互相挡住阳光照射。
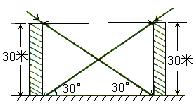
图2
二、选择题。
9. 某商品价格为a元,降价10%后,又降价10%,销售猛增,商店决定再提价20%,提价后这种商品的价格为( )
A. a元 B. 1.08a元 C. 0.972a元 D. 0.96a元
10. 小李买了20本练习本,店主给他八折优惠,结果便宜了32元,则每本练习本的标价是( )
A. 2元 B. 4元 C. 8元 D. 6元
11. 小王在一次野外活动中捡到一块矿石,回家后,他使用一把刻度尺,一只圆柱形的玻璃杯和足量的水,就测量出这块石头的体积,如果他量出玻璃杯的内直径d,把矿石完全浸在水中,测出杯中水面上升了的高度为h,则小王的这块石头的体积是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
12. 如图3,边长为12m的正方形塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3m,现在用长为4m的绳子将一头羊拴在其中的一棵树上,为了使羊在草地上活动区域的面积最大,应将绳子拴在( )
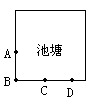
图3
A. A处 B. B处 C. C处 D. D处
13. 如图4,在正方形铁片上剪下一个圆形和扇形,使之恰好围成一个圆锥模型,设圆的半径为r,扇形的半径为R,则圆形的半径与扇形半径之间的关系是( )
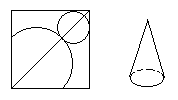
图4
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
14. 如图5在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a m,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距离地面的距离NB为b m,梯子的倾斜为45°,这间房间的宽AB一定是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
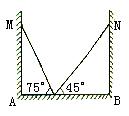
图5
三、
15. 某下岗工人在再就业中心的扶持下,创办了“润扬”报刊零售点,对经营的某种晚报,该工人提供了如下信息:
①买进每份0.2元,卖出每份0.3元;
②一个月内(以30天计),有20天每天可以卖出200份,其中10天每天只能卖出120份;
③一个月内,每天从报社买进的报纸份数必须相同,当天卖不掉的报纸,以每份0.1元退回给报社。
(1)填表:
| 一个月内每天买进该种晚报的份数 | 100 | 150 |
| 当月利润(单位:元) |
(2)设每天从报社买进该晚报x份(![]() )时,月利润为y元,试求出y与x的函数关系式,并求月利润的最大值。
)时,月利润为y元,试求出y与x的函数关系式,并求月利润的最大值。
16. 足球比赛的记分规则为:胜一场得3分,平一场得1分,输一场得0分,一支球队在某个赛季中共需比赛14场中,现已比赛了8场,输了1场,得17分。
请问:
(1)前8场球比赛中,这支球队共胜了多少场?
(2)这支球队打满14场赛,最高能得多少分?
(3)通过比赛情况的分析,这支球队打满14场比赛得分不低于29分,就可以达到预期目标,请你分析一下,在后面的六场赛中这支球队至少要胜几场,才能达到预期目标。
17. 某农场为防风沙在一山坡上种植一片树苗,并安装了自动喷灌设备,一瞬间,喷出的水流呈抛物线。如图6所示,建立直角坐标系,已知喷水头B高出地面1.5米,喷水管与山坡所成的夹角∠BOA约为63°,水流最高点C的坐标为(2,3.5)。
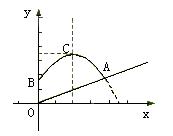
图6
(1)求此水流抛物线的解析式;
(2)求山坡所在的直线OA的解析式(解析式中的系数精确到0.1);
(3)计算水喷出后落在山坡上的最远距离OA(精确到0.1米)
18. 某生活小区的居民筹集资金1600元,计划一块上、下两底分别为10m、20m的梯形空地上种植花木(如图7)。

图7
(1)他们在△AMD和△BMC地带上种植太阳花,单价为8元/m2,当△AMD地带种满花后,(图7中阴影部分)共花了160元,请计算种满△BMC地带所需的费用。
(2)若其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/m2和10元/m2,应选择种哪种花木,刚好用完所筹集的资金?
19. 我市某中学要印制本校高中招生的录取通知书,有两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而制版费900元则六折优惠,且甲乙两厂都规定:一次印刷的数量至少是500份。
(1)分别求两个印刷厂的收费y(元)与印刷数量x(份)的函数关系,并指出自变量x的取值范围。
(2)如何根据印刷的数量选择比较合算的方案?如果这个中学要印制2000份录取通知书,那么应当选择哪一个厂?需要多少费用?
请做完之后,再看答案
【试题答案】
一、填空:
1. 40 2. 应选方案(2)
3. ![]() 4. 800
4. 800
5. 5 6. 16.11亿元
7. 约222cm 8. 30![]() 米≈52米
米≈52米
二、选择:
9. C 10. C 11. A 12. B
13. D 14. D
三、解答题:
15. (1)300 390
(2)![]()
当x=200时,y最大值为440元
16. (1)答:前8场比赛中,这个球队共胜了5场
(2)最高能得17+(14-8)×3=35分
(3)由题意得:以后的6场比赛中,只要得分不低于12分即可,故胜不少于4场一定能达到目标,而胜3场平3场,正好达到预期目标,所以在以后的比赛中这个球队至少要胜3场
17. (1)设![]() ,
,
由题意得:![]()
将B(0,1.5)代入得![]()
∴抛物线的解析式为![]()
或![]()
(2)∠AOX=27°,设坡面所在直线上一点坐标为(x,y)
则![]()
即坡面OA所在直线方程为![]()
(3)由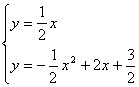
解得![]() ,∴
,∴![]() ≈4.2米
≈4.2米
答:略。
18. 解:(1)∵四边形ABCD是梯形,
∴AD∥BC,∴△AMD∽△CMB
∴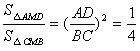
∵种植△AMD地带花费160元,∴![]()
∴![]() ,
,
△BMC地带的花费为80×8=640(元)
(2)解设△AMD,△BMC的高分别为h1,h2,梯形ABCD的高为h,
∵![]() ,∴
,∴![]()
又![]()
∴![]()
∴![]()
∴160+640+80×12=1760(元)
160+640+80×10=1600(元)
∴应种植茉莉花刚好用完所筹资金。
19. 解:(1)![]()
![]()
![]()
![]()
(2)由(1)得:
![]()
当![]()
即![]() 时,费用相同
时,费用相同
当![]() 时,甲便宜,当
时,甲便宜,当![]() 时,乙便宜。
时,乙便宜。
则当![]() 时,应选甲
时,应选甲
要:![]() (元)
(元)