2005年中考北师大版八年级(下)有关知识卷
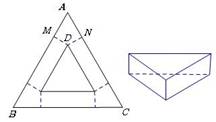 6.用一块等边三角形的硬纸片(如图1)做一个底面为等边三角形且高相等的无盖的盒子(边缝忽略不计,如图2),在
6.用一块等边三角形的硬纸片(如图1)做一个底面为等边三角形且高相等的无盖的盒子(边缝忽略不计,如图2),在![]() 的每个顶点处各需剪掉一个四边形,其中四边形
的每个顶点处各需剪掉一个四边形,其中四边形![]() 中,
中,![]() 的度数为
的度数为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.函数![]() 中,自变量
中,自变量![]() 的取值范围是
.
的取值范围是
.
![]()
![]()
![]()
![]()
![]() 10.用“ 、 ”定义新运算:对于任意实数
10.用“ 、 ”定义新运算:对于任意实数![]() ,
,![]() ,都有
,都有![]()
![]() =
=![]() 和
和![]()
![]() =
=![]() .例如.
.例如.
3![]()
![]()
![]()
![]() 2=3,3 2=2,则(2006 2005) (2004 2003)=
.
2=3,3 2=2,则(2006 2005) (2004 2003)=
.
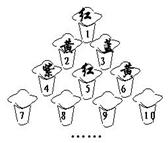 12.把编号为1,2,3,4,…的若干盆花按右图所示摆放,
12.把编号为1,2,3,4,…的若干盆花按右图所示摆放,
花盆中的花按红、黄、蓝、紫的颜色依次循环排列.围
第8行的从左边数死6盆花的颜色为 色.
14.先化简,再求值:![]() ,其中
,其中![]()
16.解不等式![]() .
.
20.甲、乙两名运动员在6次百米跑训练中的成绩如下.(单位:秒)
| 甲 | 10.8 | 10.9 | 11.0 | 10.7 | 11.2 | 10.8 | |
| 乙 | 10.9 | 10.9 | 10.8 | 10.8 | 10.5 | 10.9 |
请你比较这两组数据中的众数、平均数、中位数,谈谈你的看法
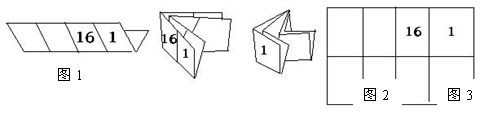
22.印刷一本书,为了使装订成书后页码恰好为连续的自然数,可按如下方法操作:先将一张整版的纸,对折一次成为4页,再对折一次为8页,连续对折三次为16页,……;然后再排页码.如果想设计一本16页的毕业纪念册,请你按图1、图2、图3(图中的1,16表示页码)的方法折叠,在图4中填上按这种折叠方法得到各页的相应位置上的页码.
 |
 山东
山东
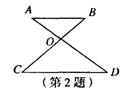
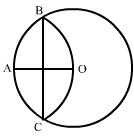
2.如图,AB∥CD,AD,BC相交于O,∠BAD=35°,∠BOD=76°,
则∠C的度数是( )
(A) 31° (B) 35° (C) 41° (D) 76°
3.某学校为了了解学生的课外阅读情况,随机调查了50
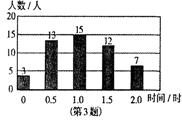 名学生,得到他们在某一天各自课外阅读所用时间的
名学生,得到他们在某一天各自课外阅读所用时间的
数据,结果见下图.根据此条形图估计这一天该校学
生平均课外阅读时为( )
(A)0.96时 (B)1.07时 (C)1.15时 (D)1.50时
5.班级组织有奖知识竞赛,小明用100元班费购买笔记本和钢笔共30件,已知笔记本每本2元,钢笔每支5元,那么小明最多能买钢笔( )
(A)20支 (B)14支 (C)13支 (D)10支
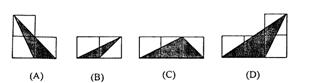
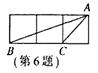 6.如图,小正方形的边长均为l,则下列图中的三角形(阴影部分)与△ABC相似的是( )
6.如图,小正方形的边长均为l,则下列图中的三角形(阴影部分)与△ABC相似的是( )
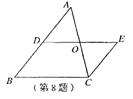 8.如图,△ABC中,∠ABC=∠BAC,D是AB的中点,EC∥AB,
8.如图,△ABC中,∠ABC=∠BAC,D是AB的中点,EC∥AB,
DE∥BC,AC与DE交于点O.下列结论中,不一定成立的是( )
(A)AC=DE (B)AB=AC
(C)AD=EC (D)OA=OE
已知![]()
20.(本题满分10分)
为了从甲、乙两名学生中选择一人参加电脑知识竞赛,在相同条件下对他们的电脑知识进行了10次测验,成绩如下:(单位:分)
| 甲成绩 | 76 | 84 | 90 | 84 | 81 | 87 | 88 | 81 | 85 | 84 |
| 乙成绩 | 82 | 86 | 87 | 90 | 79 | 81 | 93 | 90 | 74 | 78 |
(1)请完成下表:
|
| 平均数 | 中位数 | 众数 | 方差 | 85分以上的频率 |
| 甲 | 84 | 84 | 14.4 | 0.3 | |
| 乙 | 84 | 84 | 34 |
(2)利用以上信息,请从三个不同的角度对甲、乙两名同学的成绩进行分析.
23.(本题满分12分)
某水果批发市场香蕉的价格如下表:
| 购买香蕉数 (千克) | 不超过 20千克 | 20千克以上但不超过40千克 | 40千克以上 |
| 每千克价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克(第二次多于第一次),共付款264元,请问张强第一次、第二次分别购买香蕉多少千克?
河南省
7、函数y=中,自变量x的取值范围是__________
 10、已知:如图,AC⊥BC,BD⊥BC,AC>BC>BD,请你添加一个条件使△ABC∽△CDB,你添加的条件是___________________________。
10、已知:如图,AC⊥BC,BD⊥BC,AC>BC>BD,请你添加一个条件使△ABC∽△CDB,你添加的条件是___________________________。
16、已知x=+1,求x+1-的值。
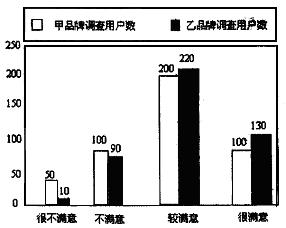
17、下图反映了被调查用户对甲、乙两种品牌空调售后服务的满意程度(以下称:用户满意程度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分。
⑴、分别求甲、乙两种品牌用户满意程度分数的平均值(计算结果精确到0.01分);
⑵、根据条形统计图及上述计算结果说明哪个品牌用户满意程度较高?该品牌用户满意程度分数的众数是多少?
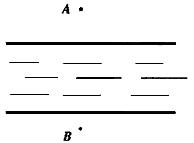 21、如图是一条河,点A为对岸一棵大树,点B是该岸一根标杆,且AB与河岸大致垂直,现有如下器材:一个卷尺,若干根标杆,根据所学的数学知识,设计出一个测量A、B两点间距离的方案,在图上画出图形,写出测量方法。
21、如图是一条河,点A为对岸一棵大树,点B是该岸一根标杆,且AB与河岸大致垂直,现有如下器材:一个卷尺,若干根标杆,根据所学的数学知识,设计出一个测量A、B两点间距离的方案,在图上画出图形,写出测量方法。
河北
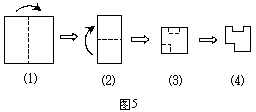 9、将一正方形纸片按图5中⑴、⑵的方式依次对折后,再沿⑶中的虚线裁剪,最后将⑷中的纸片打开铺平,所得图案应该是下面图案中的( )
9、将一正方形纸片按图5中⑴、⑵的方式依次对折后,再沿⑶中的虚线裁剪,最后将⑷中的纸片打开铺平,所得图案应该是下面图案中的( )
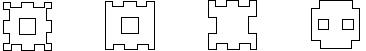
11、分解因式1-4x2= .
16、(本小题满分7分)
已知![]() ,求
,求![]() ·
·![]() 的值。
的值。
17、(本小题满分7分)
如图9,晚上,小亮在广场上乘凉。图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯。
⑴请你在图中画出小亮在照明灯(P)照射下的影子;
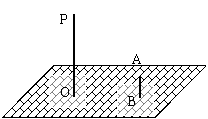 ⑵如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度。
⑵如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度。
 20、(本小题满分8分)
20、(本小题满分8分)
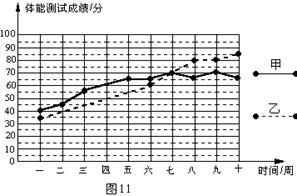
图11是连续十周测试甲、乙两名运动员体能训练情况的折线统计图。教练组规定:体能测试成绩70分以上(包括70分)为合格。
⑴请根据图11中所提供的信息填写右表:
⑵请从下面两个不同的角度对运动员体能测试结果进行判断:
①依据平均数与成绩合格的次数比较甲和乙, 的体能测试成绩较好;
| 平均数 | 中位数 | 体能测试成 绩合格次数 | |
| 甲 | 65 | ||
| 乙 | 60 |
②依据平均数与中位数比较甲和乙, 的体能测试成绩较好。
⑶依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好。
黑龙江
2 函数y=中,自变量x的取值范围是 ;
12.已知BD、CE是△ABC的高,直线BD、CE相交所成的角中有一个角为500,则∠BAC等于 度.
16.在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在地面上的影长为40米,则古塔高为---------------------------------------------------------------- ( )
(A)60米 (B)40米 (C)30米 (D)25米
17.不等式组![]() 的解集是------------------------------------------ ( )
的解集是------------------------------------------ ( )
(A)x≤3 (B)l<x≤3 (C)x≥3 (D)x>1
先化简,再求值:+,其中x=-2.
24.(本题7分)
为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了如下统计表和频率分布直方图,请你根据统计表和频率分布直方图回答下列问题:
| 平均成绩 | 0 | l | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | O | 1 | 3 | 3 | 4 | 6 | 1 | 0 |
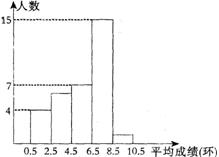
(1)参加这次射击比赛的队员有多少名?
(2)这次射击比赛平均成绩的中位数落在频率分布直方图的哪个小组内?
(3)这次射击比赛平均成绩的众数落在频率分布直方图的哪个小组内?
25.(本题8分)
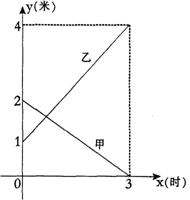
某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
27.(本题10分)
某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
| A | B | |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
(1)该公司对这两种户型住房有哪几种建房方案?
(2)该公司如何建房获得利润最大?
(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
注:利润=售价-成本
大连
5.张华同学的身高为1.6米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树的影长为6米,则这棵树的高为( )
A、3.2米 B、4.8米 C、5.2米 D、5.6米
6.要调查某校初三学生周日的睡眠时间,选取调查对象最合适的是( )
A、
 选取一个班级的学生
B、选取50名男生
选取一个班级的学生
B、选取50名男生
C、选取50名女生 D、随机选取50名初三学生
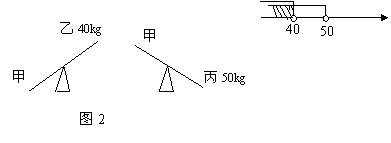
8.图2是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),
则甲的体重的取值范围在数轴上表示正确的是( )
 | |||
 | |||
A B
 | |||
 | |||
15.已知![]() ,试说明在右边代数式有意义的条件下,不论x为何值,y的值不变。
,试说明在右边代数式有意义的条件下,不论x为何值,y的值不变。
18.为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图6),图中从左到右依次为第1、2、3、4、5组。
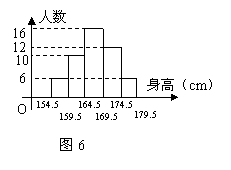 (1)求抽取了多少名男生测量身高。
(1)求抽取了多少名男生测量身高。
(2)身高在哪个范围内的男生人数最多?(答出是
第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm
及170cm以上的人数。
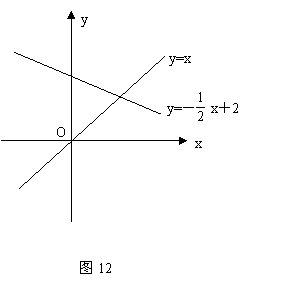 25.如图12,P是y轴上一动点,是否
25.如图12,P是y轴上一动点,是否
存在平行于y轴的直线x=t,使它与直线
y=x和直线![]() 分别交于点D、E
分别交于点D、E
(E在D的上方),且△PDE为等腰直角三
角形。若存在,求t的值及点P的坐标;
若不存在,请说明原因。
陕西省
3.化简![]() 的结果是( )
的结果是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.应中共中央总书记胡锦涛同志的邀请,中国国民党主席连战先生、亲民党主席宋楚瑜先生分别从台湾来大陆参观访问,先后来到西安,都参观了新建成的“大唐芙蓉园”。该园占地面积约为800000m2,若按比例尺1:2000缩小后,其面积大约相当于( )
A.一个篮球场的面积 B.一张乒乓球台台面的面积
C.《陕西日报》的一个版面的面积 D.《数学》课本封面的面积
12.分解因式:a3-2a2b+ab2=________。
20(本题满分8分)
为了了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班50名学生进行了调查,有关数据如下表:
| 每周做家务的时间(小时) | 0 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 人数(人) | 2 | 2 | 6 | 8 | 12 | 13 | 4 | 3 |
根据上表中的数据,回答下列问题:
(1) 该班学生每周做家务劳动的平均时间是多少小时?
(2) 这组数据的中位数、众数分别是多少?
(3) 请你根据(1)、(2)的结果,用一句话谈谈自己的感受。
22.(本题满分8分)
阅读:我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图①.
观察图①可以得出:直线=1与直线y=2x+1的交点P的坐标(1,3)就是方程组![]() 的解,所以这个方程组的解为
的解,所以这个方程组的解为![]()
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图③。
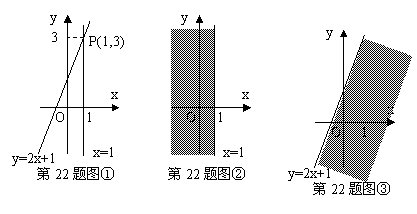
回答下列问题:
(1)
在直角坐标系(图④)中,用作图象的方法求出方程组![]() 的解;
的解;
(2)
用阴影表示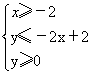 ,
,
所围成的区域。
安徽
3. 根据下图所示,对a、b、c三中物体的重量判断正确的是 ( )
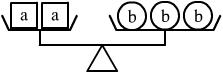
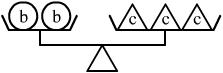
A. a<c B. a<b C. a>c D. b<c
4. 下列图中能过说明∠1>∠2的是 ( )
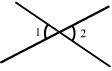
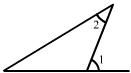
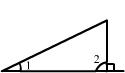
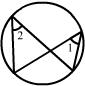
9.某市社会调查队对城区内一个社区居民的家庭经济状况进行调查. 调查的结果是, 该社区工有500户, 高收入\中等收入和低收入家庭分别有125户\280户和95户. 已知该市有100万户家庭下列表书增却的是 ( )
A. 该市高收入家庭约25万户
 B. 该市中等收入家庭约56万户
B. 该市中等收入家庭约56万户
C. 该市低收入家庭业19万户
D. 因城市社区家庭经济状况好,所以不能据此估计全市所有家庭经济状况
15. 请将下面的代数式尽可能化简, 再选择一个你喜欢的数(要合适哦!)代入求值:
![]()
16. 解不等式组![]()
19. 2004年12月28日, 我国第一条城际铁路——合宁铁路(合肥至南京)正式开工建设. 建成后, 合肥至南京的铁路运行里程将由目前的312km缩短至154km, 设计时速是现行时速的2.5倍, 旅客列车运行时间将因此缩短约3.13h. 求合宁铁路的设计时速.
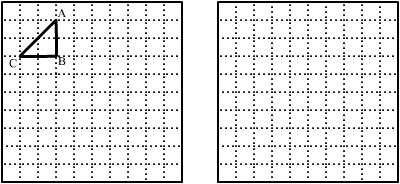
22. 图(1)是一个10×10格点正方形组成的网格. △ABC是格点三角形(顶点在网格交点处), 请你完成下面两个问题:
(1) 在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2,
且△A1B1C1与△ABC的相似比是2, △A2B2C2与△ABC的相似比是![]() .
.
(2) 在图(2)中用与△ABC、△A1B1C1、△A2B2C2全等的格点三角形(每个三角形至少使用一次), 拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.
嘉兴
10.某市为处理污水需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时每天比原计划多铺设10米,结果提前20天完成任务。设原计划每天铺设管道x米,则可得方程( )
![]() (A)
(A)![]() (B)
(B)![]()
 (C)
(C)![]() (D)
(D)![]()
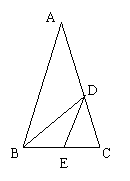
18.顶角为36°的等腰三角形称为黄金三角形。如
图,△ABC、△BDC、△DEC都是黄金三角形
已知AB=1,则DE=___________________
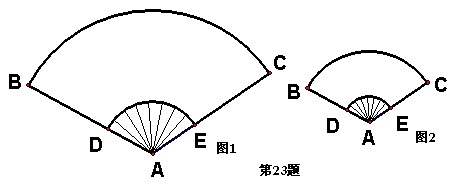
23.(本题12分)某校研究性学习小组在研究相似图形时,发现相似三角形的定义、判定及其性质,可以拓展到扇形的相似中去。例如,可以定义:“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”;相似扇形有性质:弧长比等于半径比、面积比等于半径比的平方…。请你协助他们探索这个问题。
(1) 写出判定扇形相似的一种方法:若_____________________________,则两个扇形相似;
(2) 有两个圆心角相等的扇形,其中一个半径为a、弧长为m,另一个半径为2a,则它的弧长为_________________;
(3) 如图1是一完全打开的纸扇,外侧两竹条AB和AC的夹角为120°,AB为30cm,现要做一个和它形状相同、面积是它一半的纸扇(如图2),求新做纸扇(扇形)的圆心角和半径。
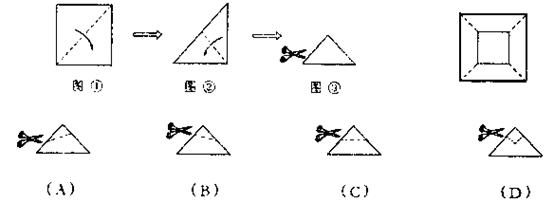
8.将一张正方形纸片,沿图的虚线对折,得图,然后剪去一个角,展开铺平后的图形如右图所示,则图中沿虚线的剪法是( )
 24.(本题满分12分)
24.(本题满分12分)
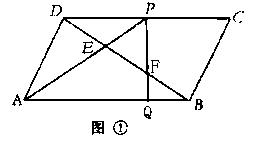
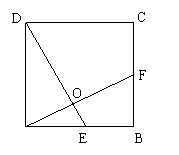
E、F为![]() ABCD的对角线DB上三等分点,连AE并延长交DC于P,连PF并延长交AB于Q,如图①
ABCD的对角线DB上三等分点,连AE并延长交DC于P,连PF并延长交AB于Q,如图①
(1) 在备用图中,画出满足上述条件的图形,记为图②,试用刻度尺在图①、②中量得AQ、BQ的长度,估计AQ、BQ间的关系,并填入下表
长度单位:cm
| AQ长度 | BQ长度 | AQ、BQ间的关系 | |
| 图①中 | |||
| 图②中 |
由上表可猜测AQ、BQ间的关系是__________________
(2) 上述(1)中的猜测AQ、BQ间的关系成立吗?为什么?
(3)
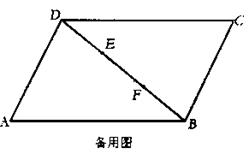
若将![]() ABCD改为梯形(AB∥CD)其他条件不变,此时(1)中猜测AQ、BQ间的关系是否成立?(不必说明理由)
ABCD改为梯形(AB∥CD)其他条件不变,此时(1)中猜测AQ、BQ间的关系是否成立?(不必说明理由)
22.(本小题8分)
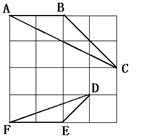 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在
边长为1的小正方形的顶点上.
(1)填空:∠ABC= °,BC= ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.
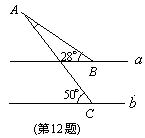 12. 如图所示,直线a∥b,则∠A= ▲ 度.
12. 如图所示,直线a∥b,则∠A= ▲ 度.
15. 在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式![]() ,因式分解的结果是
,因式分解的结果是![]() ,若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式
,若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式![]() ,取x=10,y=10时,用上述方法产生的密码是: ▲ (写出一个即可).
,取x=10,y=10时,用上述方法产生的密码是: ▲ (写出一个即可).
(2) 解方程:![]() .
.
21. 一个矩形,两边长分别为xcm和10cm,如果它的周长小于80cm,面积大于100cm2.求x的取值范围.
22. 某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1) 写出所有选购方案(利用树状图或列表方法表示);
 (2) 如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(2) 如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.
玉溪市
5.不等式组![]() 的解集表示在数轴上正确的 ( )
的解集表示在数轴上正确的 ( )
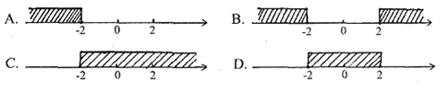
10.多项式![]() 是一个完全平方式,则M等于(填一个即可)
。
是一个完全平方式,则M等于(填一个即可)
。
潍坊
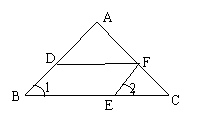 4.如图,在
4.如图,在![]() 中,
中,![]()
![]() 分别在
分别在![]() 上,且
上,且![]() ∥
∥![]() ,要使
,要使![]() ∥
∥![]() ,只需再有下列条件中的( )即可.
,只需再有下列条件中的( )即可.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.若![]() 求
求![]() 的值是( ).
的值是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.某种品牌的同一种洗衣粉有![]() 三种袋装包装,每袋分别装有400克、300克、200克洗衣粉,售价分别为
三种袋装包装,每袋分别装有400克、300克、200克洗衣粉,售价分别为![]() 元、2.8元、1.9元.
元、2.8元、1.9元.![]() 三种包装的洗衣粉每袋包装费用(含包装袋成本)分别为0.8元、0.6元、0.5元.厂家销售
三种包装的洗衣粉每袋包装费用(含包装袋成本)分别为0.8元、0.6元、0.5元.厂家销售![]() 三种包装的洗衣粉各1200千克,获得利润最大的是( ).
三种包装的洗衣粉各1200千克,获得利润最大的是( ).
A.![]() 种包装的洗衣粉 B.
种包装的洗衣粉 B.![]() 种包装的洗衣粉
种包装的洗衣粉
C.![]() 种包装的洗衣粉 D.三种包装的都相同
种包装的洗衣粉 D.三种包装的都相同
15.(A题) 某电视台在每天晚上的黄金时段的3分钟内插播长度为20秒和40秒的两种广告,20秒广告每次收费6000元,40秒广告每次收费10000元.若要求每种广告播放不少于2次,且电视台选择收益最大的播放方式,则在这一天黄金时段3分钟内插播广告的最大收益是__________元.
20.(本题满分9分)
为了加强学生的交通安全意识,某中学和交警大队联合举行了“我当一日小交警”活动,星期天选派部分学生到交通路口值勤,协助交通警察维护交通秩序.若每一个路口安排4人,那么还剩下78人;若每个路口安排8人,那么最后一个路口不足8人,但不少于4人.求这个中学共选派值勤学生多少人?共有多少个交通路口安排值勤?
 芜湖市
芜湖市
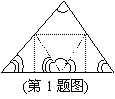
1. 亲爱的同学们,在我们的生活中处处有数学的身影.请看图,
折叠一张三角形纸片,把三角形的三个角拼在一起,就得到
一个著名的几何定理,请你写出这一定理的结论:“三角形
的三个内角和等于_______°.”
8.
已知数据x1,x2,…,xn的平均数是![]() ,则一组新
,则一组新
数据x1+8,x2+8,…,xn+8的平均数是____.
25. 分式![]() 的值为0,则x的取值为
(
).
的值为0,则x的取值为
(
).
A.x=-3 B.x=3
C.x=-3或x=1 D.x=3或x=-1
33.
通过市场调查,一段时间内某地区特种农产品的需求量y(千克)与市场价格x(元/千克)存在下列函数关系式:y=![]() (0<x<100);又已知该地区农民的这种农产品的生产数量z(千克)与市场价格x(元/千克)成正比例关系:z=400x(0<x<100),现不计其它因素影响,如果需求数量y等于生产数量z时,即供需平衡,此时市场处于平衡状态.
(0<x<100);又已知该地区农民的这种农产品的生产数量z(千克)与市场价格x(元/千克)成正比例关系:z=400x(0<x<100),现不计其它因素影响,如果需求数量y等于生产数量z时,即供需平衡,此时市场处于平衡状态.
(1) 根据以上市场调查,请你分析当市场处于平衡状态时,该地区这种农产品的市场价格与这段时间内农民的总销售收入各是多少?(4分)
(2) 受国家“三农”政策支持,该地区农民运用高科技改造传统生产方式,减少产量,以大力提高产品质量.此时生产数量z与市场价格x的函数关系发生改变,而需求函数关系未发生变化,当市场再次处于平衡状态时,市场价格已上涨了a(0<a<25)元,问在此后的相同时间段内该地区农民的总销售收入是增加了还是减少了?变化多少?(4分)
39. 如图①,在平面直角坐标系中,AB、CD都垂直于x轴,垂足分别为B、D且AD与B相交于E点.已知:A(-2,-6),C(1,-3)
(1) 求证:E点在y轴上;(4分)
(2) 如果AB位置不变,再将DC水平向右移动k(k>0)个单位,此时AD与BC相交于E′点,如图②,求△AE′C的面积S关于k的函数解析式.(4分)

南通市
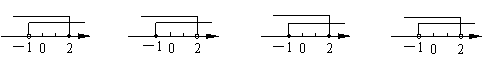 6. 不等式组
6. 不等式组![]() 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是
8. 已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF
的一边长为4 cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似
A.2 cm,3 cm B.4 cm,5 cm
C.5 cm,6 cm D.6 cm,7 cm
10.某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形
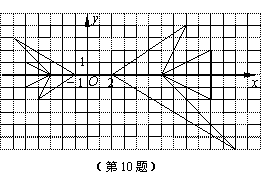 (如图所示).
(如图所示).
则小鱼上的点(a,b)对应大鱼上的点
A.(-2a,-2b) B.(-a,-2b)
C.(-2b,-2a) D.(-2a,-b)
16.计算![]() .
.
20.(本小题7分)
解方程 ![]() .
.
某市政府切实为残疾人办实事,在区道路改造中为盲人修建一条长3000m的盲道,根据规 划设计和要求,该市工程队在实际施工时增加了施工人员,每天修建的盲道比原计划增加50%,结果提前2天完成,则实际每天修建盲道__________m.
先化简,再求值:![]() ,其中
,其中![]() ,
,![]() .
.