常州市新桥中学2006年中考数学模拟测试二

班级____姓名___________得分______

一、细心填一填

1．（1）－的相反数是___________，16的算术平方根是___________.

（2）分解因式x²－4x＋4＝____________.

2．上海市统计局3月16日公布的1%人口抽样调查主要数据公报说,2005年11月1日零时,全市常住人口为1778万人,这个数据用科学记数法表示是___________万人.

3．函数的自变量x的取值范围是____________________；

4．菱形ABCD的对角线AC＝6cm，BD＝8cm，则菱形ABCD的面积S＝___________.

5．如图，⊙O为△ABC的外接圆，且∠A＝30°，AB＝8cm，BC＝5cm，则⊙O的半径＝___________cm，点O到AB的距离为___________cm.。

6．如图，为了测量小河的宽度，小明先在河岸边任意取一点A，再在河岸这边取两点B、C，测得∠ABC＝45°，∠ACB＝30°，量得BC为20米，根据以上数据，请帮小明算出河的宽度d＝_________________米（结果保留根号）。

7．若某一圆锥的侧面展开图是一个半径为8的半圆，则这个圆锥的底面半径是________.

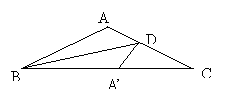
8．已知△ABC中，AB=AC，∠BAC=120°，点D是边AC上一点，连BD，若沿直线BD翻折，点A恰好落在边BC上，则AD：DC=　　　　  。

9．小红从A地去B地，以每分钟2米的速度运动，她先前进1米，再后退2米，又前进3米，再后退4米，……依此规律走下去，则1小时后她离A地相距___________米.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　

 第8题

二、精心选一选

10．下列运算正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A． x²＋x²＝x⁴　　B．(a－1)²＝a²－1　 C．a²·a³＝a⁵　　 D．3x＋2y＝5xy　

11．化简的结果是　　　　　　　　　　　　　　　　　　　 　　　　　 （　　）

A．－2　　　　　 B．±2　　　　　　 C．2　　　　　　 D．4

12．下列几项调查，适合作普查的是　　　　　　　　　　　　　　　　　　　  （　　）

A．调查常州超市里酸奶的细菌含量是否超标　 B．调查市区5月1日的空气质量

C．调查你所在班级全体学生的身高　　　　　 D．调查全市中学生每人每周的零花钱

13．已知⊙O₁的半径为3cm，O₁到直线l的距离为2cm，则直线l与⊙O₁的位置关系为（　　）

A．相交　　　　  B．相切　　　　　  C．相离　　　　  D．不相交

14．“五一”黄金周期间，为了促销商品，甲、乙两个商店都采取优惠措施，甲店推出八折

后再打八折，乙店则一次性六折优惠，对于同一种商品，下列结论正确的是　　　（　　）

A．甲比乙优惠　　B．乙比甲优惠　　 C．两店同样优惠　 D．无法比较两店的优惠程度

15．如图1，在边长为a的正方形中剪去一个边长为b的小正形（a＞b），把剩下部分拼成一个梯形（如图2），利用这两幅图形面积，可以验证的公式是　　　　　　　  （　　）

A．a²＋b²＝(a＋b)(a－b)　　　　　　 B．(a－b)²＝a²－2ab＋b²

C．(a＋b)²＝a²＋2ab＋b²　　　　　　  D．a²－b²＝(a＋b)(a－b)

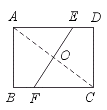
16．如图，矩形ABCD的边长AB＝6，BC＝8，将矩形沿EF折叠，使C点与A点重合，

则折痕EF的长是……………………………………………………………………（　　）

A．7．5　 　　　　　B．6　　　　　　C．10　　　　　　 D．5

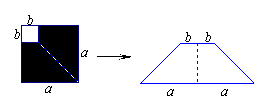第15题　　　　　　　　　　　　　　　　　　　 第16题

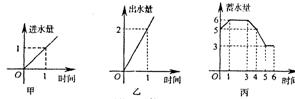
17.水池有2个进水口，1个出水口，每个进水口进水量与时间的关系如图甲所示，出水口出水量与时间的关系如图乙所示．某天O点到6点，该水池的蓄水量与时间的关系如图丙．

下列论断：①O点到1点，打开两个进水口，关闭出水口；②1点到3点，同时关闭两个进水口和一个出水口；③3点到4点，关闭两个进水口，打开出水口；④5点到6点，同时打开两个进水口和一个出水口．其中，可能正确的论断是　　　　　　　　　　　 (　　)

A．①③　　　　　  B．①④　　　　　 C．②③　　　　　  D．②④

18．如图，小刚使一长为4，宽为3的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A位置变化为，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为　　　　　 （　　）

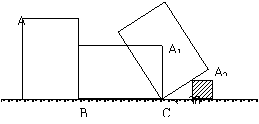
A．10　　　　  B．　　　　 C．　　　　  D．

第17题　　　　　　　　　　　　　　　　　　　 第18题

三、认真答一答

19．（1）计算：－2²＋（）⁰＋2sin30º　　　 （2）化简：÷(x－)

20．（1）解方程：　　 （2）解不等式组：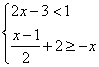

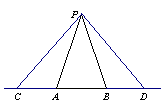
21．如图△PAB中，PA＝PB，C、D是直线AB上两点,连结PC、PD.

（1）请添加一个条件：　　　　　  ，使图中存在两个三角形全等.

（2）证明（1）的结论.

22．不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为.

（1）试求袋中蓝球的个数.

（2）第一次任意摸一个球（不放回），第二次再摸一个球，请画树状图或列表格，求两次摸到都是白球的概率.

23．如图，晚上，小亮在广场上乘凉．图中线段AB表示站立在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯．

（1）请你在图中画出小亮在照明灯（P）照射下的影子；

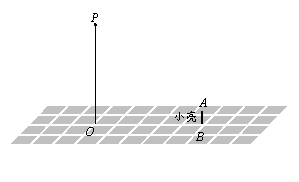（2）如果灯杆高PO＝12m，小亮的身高AB＝1.6m，小亮与灯杆的距离BO＝13m，请求出小亮影子的长度．

24.2006年3月15日, 深受海内外关注的磁浮铁路沪杭线交通项目获国务院批准.该项目

预计将于2008年建成,建成后,上海至杭州的铁路运行路程将由目前的200千米缩短至175

千米, 磁浮列车的设计速度是现行特快列车速度的3.5倍,运行时间将比目前的特快列车运

行时间约缩短1.2小时,试求磁浮铁路沪杭线磁浮列车的设计速度是每小时多少千米?

25.据2006年3月4日的<<解放日报>>报道,上海市就业促进中心发布了本市劳动者职业流

动周期分析报告,该报告说2005年上海劳动者的平均职业流动周期为46.6个月,也就是说平

均每位劳动者在一家单位连续工作近4年.下面是“不同学历劳动者的职业流动周期”与“不

同年龄段劳动者的职业流动周期”的统计图,请根据图中的有关信息回答下列问题:

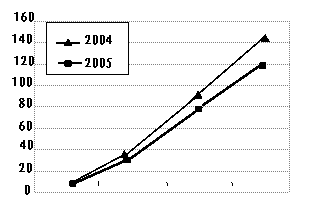
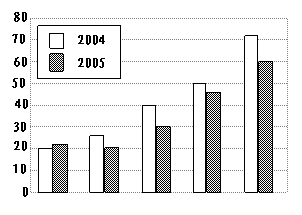
(1)从学历分析来看,2004年不同学历劳动者的职业流动周期的中位数是___________个月,2005年不同学历劳动者的职业流动周期的中位数是________个月,本市劳动者职业流动周期随着学历的增高呈_________趋势（选择“上升”或“下降”）;

(2)从年龄分析来看,本市劳动者职业流动周期随着年龄的增大呈_________趋势（选择“上升”或“下降”）,2005年的职业流动周期与2004年比较,职业流动的周期_______了(填“缩短”或“延长”), 职业流动周期低于20个月的劳动者年龄范围__________;

(3)本市劳动者,学历为________的职业流动周期最短,年龄范围为_________的职业流动周期最长;

26.已知抛物线（其中a、b、c都不等于0），它的顶点P的坐标是轴的交点是M（0，c）. 我们称以M为顶点，对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线，直线PM为L的伴随直线.

（1）求抛物线（其中a、b、c都不等于0）的伴随抛物线和伴随直

线的解析式；

（2）请直接写出抛物线的伴随抛物线和伴随直线的解析式：

　　 伴随抛物线的解析式　　　　　　　　　　　　　　　　　　　 ，

　　 伴随直线的解析式　　　　　　　　　　　　　　　　　　　　 ；

（3）若一条抛物线的伴随抛物线和伴随直线分别是，则这条抛物线的解析式是　　　　　　　　　　　　　　　 ；

27．如图，已知二次函数的图像开口向下，与x轴的一个交点为B，顶点A在直线上，O为坐标原点。

（1）证明：△AOB是等腰直角三角形；

（2）若△AOB的外接圆C的半径为1，求该二次函数的解析式；

（3）对题（2）中所求出的二次函数，在其图像上是否存在点P（点P与点A不重合），使得△POC是以PC为腰的等腰三角形，若存在，请求出点P的坐标，若不存在，请说明理由。

四、实践与探索

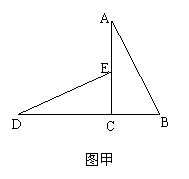
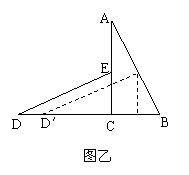
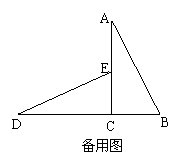
28.如图甲：ACB与DCE是全等的两个直角三角形，其中ACB=DCE=90⁰，AC=4，BC=2，点D、C、B在同一条直线上，点E在边AC上.

（1）直线DE与AB有怎样的位置关系？请证明你的结论；

（2）如图乙：若DCE沿着直线DB向右平移多少距离时，点E恰好落在边AB上，求平移距离DD′^，；

（3）在DCE沿着直线DB向右平移的过程中，使DCE与ACB的公共部分是四边形，设平移过程中的平移距离为，这个四边形的面积为，求与的函数关系式，并写出它的定义域.