常州市新桥中学2006年中考数学模拟测试三

班级____姓名___________得分______

一、细心填一填

1．—的绝对值是　　　 ，16的平方根_________，y=中x的取值范围是　　　　 。

2．分解因式：x³－4x=　　　　　　　 。

3．一粒钮扣式电池能够污染60升水，某市每年报废的钮扣式电池有近粒，若废旧电池不回收，一年报废的纽扣式电池所污染的水约 　　　　　 升（用科学记数法表示）。

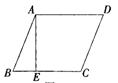
4．如图，在菱形ABCD中，AE⊥BC于E，EC＝8，cos∠B＝，则这个菱形的面积

是　　　　　　　  。

第4题　　　　　　  第5题　　　　　　　 第6题　　　　　　 第7题

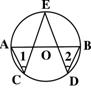
5．如图，AB是⊙O的直径，C、D、E都是⊙O上的点，则∠1＋∠2＝　　　　。

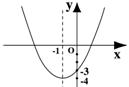
6．二次函数y＝x²＋bx＋c的图象如图所示，则y＜0时，x的取值范围是　　 　　　　　　 。

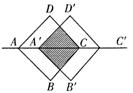
7．如图，将正方形ABCD沿AC方向移动到正方形A′B′C′D′的位置，它们的重叠部

分的面积是正方形ABCD面积的一半，若AC＝，则正方形移动的距离为 __________。

8．在地面上某一点周围有a个正三角形、b个正十二边形（a、b均不为0），恰能铺满地面，

则a＋b＝___________.

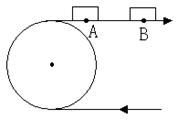
9.如图，某传送带的一个转动轮的半径为20cm，当物体从A传送20cm至B时，那么这个转动轮转了_________度.

10．在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点. 观察图中每一个正方形

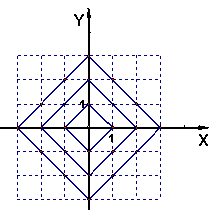（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上的整点

个数共有_________个。

第9题　　　　　　　　　　 第10题　　　　　　　　　　　　 第12题

二、精心选一选

11．下列运算正确的是　　　　　　　　　　　　　　　　　　　　　　  　　　(　　)

A．x·x³=x³ B．x²+x²=x⁴　　 C．(-4xy²)²=8x²y⁴　　　 D．(-2x²)(-4x³)=8x⁵

12．香港于1997年7月1日成为中华人民共和国的一个特别行政区，它的区徽图案（紫荆花）如图，这个图形是　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A.　轴对称图形　　　　　　　　　　　 B. 中心对称图形

C.　既是轴对称图形，也是中心对称图形 D.　既不是轴对称图形，也不是中心对称图形

13．在下面图形中， 每个大正方形网格都是由边长为1的小正方形组成，则图中阴影部分面积最大的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

A.　　 B.　　 C.　　　D.

14．一张桌子上摆放着若干个碟子，从三个方向看，三种视图如下图所示,，则这张桌子上共有碟子为　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　(　　)

A. 6个　　　　　　　 B. 8个 　　　　  C. 12个　　　　　 D. 17个

15．若a＞0，b＜－2，则点（a，b＋2）应在　　　　　　　　　　　　　　　  （　　）

A.  第一象限　　　 B. 第二象限　　　 C. 第三象限　　　　D. 第四象限

16．现往一塑料圆柱形杯子(重量忽略不计)中匀速注水，已知10秒钟能注满杯子，之后注

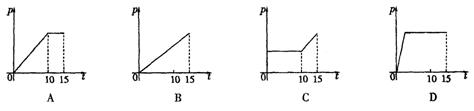入的水会溢出，下列四个图象中，能反映从注水开始，15秒内注水时间t与杯底压强P的

图象是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　   (　　)

17．如图给出的是2006年某月的日历表，任意圈出一竖列上相邻的三个数，请你运用方程思想来研究，发现这三个数的和不可能是　　　　　　　　　　　　　　　　　 （　　）

A．69　　　　　　　 B．54　　　 　　　　 C．27　　　　　　　 D．40

18．如图直角梯形ABCD中，AD∥BC，AB⊥BC，AD＝2，BC＝3，将腰CD以D为中心逆时针旋

转90°至ED，连AE、CE，则△ADE的面积是　　　　　　　　　　　　　　　  （　　）

A．1　　　　　　　  B．2　　　　　　　　 C．3　　　　　　　  D．不能确定

日　一　二　三　四　五　六 1　 2　 3　 4　 5　 6 7　　8　 9　10　11　12　13 14　15　16　17　18　19　20 21　22　23　24　25　26　27 28　29　30　31

第17题　　　　　　　　　　 第18题　　　　　　　　 第19题

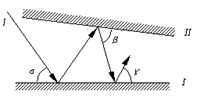
19.如图，光线l照射到平面镜I上，然后在平面镜I、II之间来回反射，已知∠=55°，∠=75°，则∠为　　　　　　　　　　　　　　　　　　　　　　　　　  （ 　 ）

A．50° 　　　　　　　B．55° 　　　　　　C．60°　 　　　　D．65°

三. 认真答一答

20.（1）计算：　　 （2）化简：

21.（1）解方程：　　　 （2）解不等式组：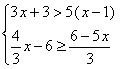

22．如图，矩形ABCD中，O是AC与ＢＤ的交点，过O点的直EF与AB、CD的延长线分别交于E、F。

（1）求证：△BOE≌△DOF

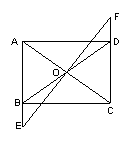（2）当EF与AC满足么条件时，四边形AECF是菱形，并明你的结论。

　　　　　　　　　　　　　　　　　　　 

23．今年“五一黄金周”期间，花果山风景区共接待游客约22.5万人．为了了解该景区的服务水平，有关部门从这些游客中随机抽取450人进行调查，请他们对景区的服务质量进行评分，评分结果的统计数据如下表：

档 次	第一档	第二档	第三档	第四档	第五档
分值a（分）	a≥90	80≤a<90	70≤a<80	60≤a<70	a<60
人 数	73	147	122	86	22

根据表中提供的信息，回答下列问题：

（1）所有评分数据的中位数应在第几档内？

（2）若评分不低于70分为“满意”，试估计今年“五一黄金周”期间对花果山景区服务“满意”的游客人数．

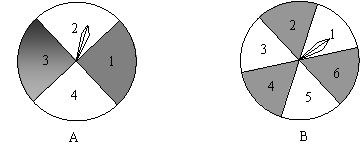
24．如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等分，每份分别标上1，2，3，4四个数字；转盘B被均匀地分成6等份，每份分别标上1，2，3，4，5，6六个数字. 有人为甲、乙两人设计了一个游戏，其规则如下：

（1）同时自由转动转盘A、B；

（2）转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止），用所指的两个数字作成积. 如果得到的积是偶数，那么甲胜；如果得到的积是奇数，则乙胜（如果转盘A指针指向3，转盘B指针指向5，3×5=15，按规则乙胜），你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由.

25.为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方

形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为,

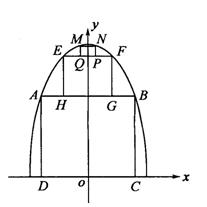正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:

(1)抛物线解析式中常数的值;

(2)正方形MNPQ的边长.

26.近两年无锡外向型经济发展迅速，一些著名跨国公司纷纷落户无锡新区，对各类人才需求不断增加，现一公司面向社会招聘人员，要求如下：

①对象：机械制造类和规划设计类人员共150名.

②机械类人员工资为600元/月，规划设计类人员为1000元/月.

（1）本次招聘规划设计人员不少于机械制造人员的2倍，若要使公司每月所付工资总额最少，则这两类人员各招多少名？此时最少工资总额是多少？

（2）在保证工资总额最少条件下，因这两类人员表现出色，公司领导决定另用20万元奖励他们，其中机械人员人均奖金不得超过规划人员的人均奖金，但不低于200元，试问规划设计类人员的人均奖金的取值范围.

27.先阅读理解下列例题,再按要求完成作业.
例题:解一元二次不等式6x²－x－2>0.
解:把6x²－x－2分解因式,得 6x²－x－2=(3x－2)(2x+1).
又6x²－x－2>0,所以(3x－2)(2x+1)>0.
由有理数的乘法法则“两数相乘，同号得正”有
（1）　或 （2）
解不等式组（1）得x>;解不等式组（2）得x<－．
所以(3x－2)(2x+1)>0的解集为x>或x<－.
因此, 一元二次不等式6x²－ｘ－2>0的解集为x>或x<－.
练习题:求不等式<0的解集.

四、动脑想一想

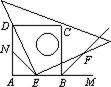
28．如图甲、乙，四边形ABCD是正方形，M是AB延长线上一点。直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM的平分线BF相交于点F。

⑴如图甲，当点E在AB边的中点位置时：

①通过测量DE，EF的长度，猜想DE与EF满足的数量关系是　　　　　；

②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是　　　　　　  ；

③请证明你的上述两猜想。

⑵如图乙，当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系。

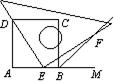　　　　　　　　　　　　　　　　　　　　　　　  甲　　　　　　　　  乙

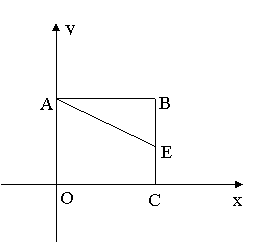
29．如图,在平面直角坐标系中,四边形ABCO是正方形,C点的坐标是(4,0)

（1）写出A、B两点的坐标；

（2）若E是线段BC上一点，且∠AEB=60^o ，沿AE折叠正方形ABCO，折叠后B点落在平面内F点处。请画出F点并求出它的坐标；

（3）若E是直线BC上任意一点，问是否存在这样的E点使正方形ABCO沿AE折叠后，B点恰好落在x轴上的某一点P处？若存在，请写出此时P点和E点的坐标。若不存在，请说明理由.