常州市新桥中学2006年中考数学模拟测试五
班级____姓名___________得分______
一、细心填一填
1.-2的倒数是______，
_______，
。
2.苏州工业园区正建设成为具有国际竞争力的高科技工业园区和现代化、园林化、国际化的新城区．2005年，全区实现地区生产总值达580.7亿元，比开发之初增长了50倍．请你用科学记数法表示2005年园区生产总值为__________________元．
3. 函数y＝中，自变量x的取值范围是__________
4.因式分解：
________________________．
5.某班有7名同学参加校“综合素质智能竞赛”，成绩(单位：分)分别是87，92，87，89，91，88，76.则它们成绩的众数是__________分，中位数_____________分．
6.如图是一口直径AB为4米，深BC为2米的圆柱形养蛙池，小青蛙们晚上经常坐在池底中心O观赏月亮，则它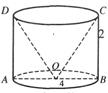
们看见月亮的最大视角
________度，(不考虑青蛙的身高).
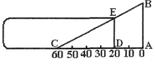
7.如图，测量小玻璃管口径的量具ABC，AB的长为12cm，AC被分为60等份．如果小玻璃管管口DE正好对着量具上20等份处(DE∥AB)，那么小玻璃管口径DE是_________cm．
8.如图两个相同的梯形重叠在一起，则上面的梯形中未重叠部分面积是_________________。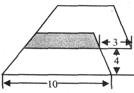
9．如图，一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分，则这串珠子被盒子遮住的部分有___ 颗.
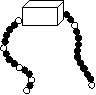
第6题 第7题 第8题 第9题
二、精心选一选
10.已知点
与点
关于
轴对称，则点的坐标为
（ ）
A．(-2，1) B．(-2，-1) C．(2，1) D．(2，-1)
11.下列四个函数中，
随增大而减小的是
（ ）
A．
B．
C．
D．
12.将方程
配方后，原方程变形为
（ ）
A．
B．
C．
D．
13．右图中水杯的俯视图是 （ ）
14.小明把自己一周的支出情况，用如图所示的统计图来表示，下面说法正确的是（ ）
A．从图中可以直接看出具体消费数额
B．从图中可以直接看出总消费数额
C．从图中可以直接看出各项消费数额占总消费额的百分比
D．从图中可以直接看出各项消费数额在一周中的具体变化情况
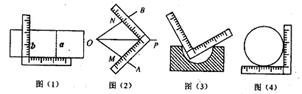
15．如图，图中的两个转盘分别被均匀地分成5个和4个扇形，每个扇形上都标有数字，同时自由转动两个转盘，转盘停止后，指针都落在奇数上的概率是 （ ）
A． B． C． D．
 |
第14题 第15题 第16题
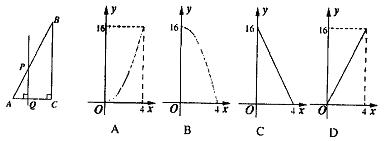
16．用一把带有刻度的直尺，①可以画出两条平行的直线a与b，如图⑴；②可以画出∠AOB的平分线OP，如图⑵所示；③可以检验工件的凹面是否为半圆，如图⑶所示；④可以量出一个圆的半径，如图⑷所示。这四种说法正确的是 （ ）
A．1个 B．2个 C．3个 D．4个
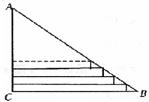
17．如图，Rt△ABC中，∠C＝900，AC＝4，BC＝8，P是AB上一动点，直线PQ⊥AC于点Q，设AQ＝x，则图中阴影部分的面积y与x之间的函数关系式的图象是 （ ）
第17题 第18题
18.某中学高二(2)班在布置“五.四”青年节联欢会会场时，需要将直角三角形彩纸裁成长度不等的矩形纸条．如图所示：在Rt△ACB 中，AC=30cm，BC=40cm．依此裁下宽度为lcm的纸条，若使裁得的纸条的长都不小于5cm，则能裁得的纸条的张数 （ ）
A．24 B．25 C．26 D．27
三、认真答一答
19（1）计算：
（2）化简：
20（1）解分式方程：
（2）解不等式组：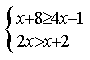
21．如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F。
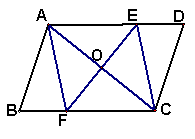求证：四边形AFCE是菱形。
22.旋转是一种常见的全等变换，图l△ABC绕点O旋转后得到
，我们称点A和点
、点B和点
、点C和点
分别是对应点，把点O称为旋转中心．
(1)观察图1，想一想，旋转变换具有哪些特点呢?请写出其中二个特点：
________________________________________________________________________
________________________________________________________________________
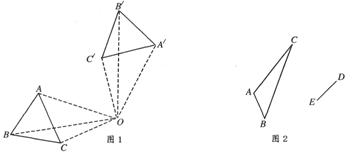
(2)图2中，△ABC旋转变换后，线段AB的对应线段为线段DE，请你利用圆规、直尺等工具，①作出旋转中心O，②作出△ABC绕点O旋转后的△DEF．(不写画法，保留作图痕迹)
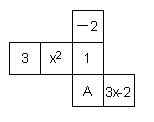23．如图是一个正方体的展开图，标注了字母A的面是正方体的正面，如果正方体的左面与右面所标注代数式的值相等，求
的值．
24．杨文与王小勇两同学玩“奇、偶手指”的游戏，两人约定：每人出右手的若干指头，至少出一根．若两人皆出奇数根指头或两人皆出偶数根指头，则杨文赢；若两人中一人出奇数根指头，另外一人出偶数根指头，则王小勇赢．试用树状图求杨文与王小勇谁赢的概率大．(注：杨文出一根指头可简单表示为：文1；王小勇出2根指头可简单表示为：勇2；其余依此类推)
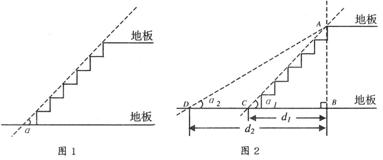25.在建筑楼梯时，设计者要考虑楼梯的安全程度，如图l，虚线为楼梯的斜度线，斜度线与地板的夹角为倾角
，一般情况下，倾角愈小，楼梯的安全程度愈高．如图2，设计者为提高楼梯的安全程度，要把楼梯的倾角由
减至
，这样楼梯占用地板的长度由
增加到
，已知
，求楼梯占用地板的长度增加了多少?(精确到0.01m)
26．施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米.现以O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）.
⑴直接写出点M及抛物线顶点P的坐标；
⑵求出这条抛物线的函数解析式，并写出自变量x的取值范围；
⑶施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上。B、C点在地面OM线上.为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下.
27．某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于建房，两种户型的建房成本和售价如下表：
| A | B | |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
(1) 该公司对这两种户型住房有哪几种建房方案?
(2) 该公司如何建房获得利润最大?
(3) 根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元(a>0)，且所建的两种住房可全部售出，该公司又将如何建房获得利润最大?
注：利润=售价-成本
四、动脑想一想
28.先阅读理解下列例题,再按要求完成练习：
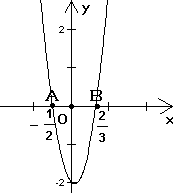
例题:已知二次函数y=6x2－x－2,当x为何值时,y>0.
解:画出二次函数y=6x2-x-2的图象,如右图:
由图象观察可知:
当x在点A的左侧与点B的右侧取值时,
抛物线y=6x2－x－2在x轴的上方,此时
二次函数y=6x2－x－2的函数值正好大于
零, 所以,当x>或x<－时,y>0.
练习: 已知二次函数y=x2－2x－3,当x为何值时,y<0.
29．如图，在平面直角坐标系中，两个函数
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动，作PQ∥x轴交直线BC于点Q，以PQ为一边向下作正方形PQMN，设它与△OAB重叠部分的面积为S。
（1）求点A的坐标。
（2）试求出点P在线段OA上运动时，S与运动时间t（秒）的关系式。
（3）在（2）的条件下，S是否有最大值？若有，求出t为何值时，S有最大值，并求出最大值；若没有，请说明理由。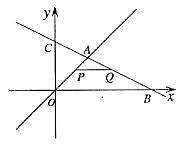
（4分）若点P经过点A后继续按原方向、原速度运动，当正方形PQMN与△OAB重叠部分面积最大时，运动时间t满足的条件是____________。