常州市新桥中学2006年中考数学模拟测试一

班级____姓名___________得分______

一、细心填一填

1.的相反数是　　　　，的平方根是　　　　.

2. （1）计算： 　　　　 ，（2）因式分解：　　　　　　　 .

3.国务院总理温家宝3月5日在十届人大四次会议上作政府报告时说，2005年我国社会主义现代化事业取得显著成就，全年国内生产总值达到18.23万亿元，将这一数字用科学记数表示为______________亿元.

4．函数y＝中，自变量x的取值范围是___________；

函数y＝中，自变量x的取值范围是___________。

5.已知反比例函数的图象经过点（-2，-3），则　　　 .

6.已知抛物线的顶点坐标为　　　　 ，当x满足____________时，y随x的增大而减小。

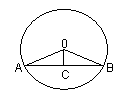
7.如图，已知AB是⊙O的一条弦，OC⊥AB于C，若AB=，r=6，则弦心距OC=　　　 ，∠AOB=　　　　  .

8.右表是近6届奥运会中国体育代表团获得的金牌数，在这组数据中，众数是　　 ，中位数是　　　　  .

第7题　　　　　　　　　  第8题　　　　　　　  　　　　第9题

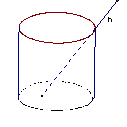
9．为了提高技术工人的能力，建设公司举办了一期岗位培训班，培训结业时出了如下一道题：有一油罐，其直径为6米，高为8米，如图，将一长为12米的金属棒置于其中，假如金属棒露在外面的长为h米，试问h的取值范围是　　　　　　　 .

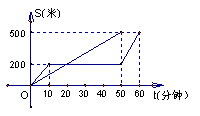
10．“龟兔赛跑”是同学们熟悉的寓言故事，如图表示龟兔赛跑路程S与时间t之间的关系，那么可以知道（1）这是一次　　　　　　 米的赛跑，赛跑中，兔子共睡了　　　　 分钟；

　　　　　　（2）龟在这次赛跑中的速度为　　　　  米/分钟.

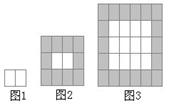
11.某体育馆用大小相同的长方形木块镶嵌地面，第一次铺2块（如图1）第二次把第一次铺的完全围起来（如图2）；第三次再把第二次铺的完全围起来（如图3）；……依次类推，第n次铺完后，用字母n表示第n次镶嵌所使用的木板数是　　　 .

第10题　　　　　　　　　　　　　　　  第11题

二、精心选一选

12. 已知两圆半径分别是1和3，圆心距为2，则两圆的位置关系是----------（　 ）

A.相离　　　　　　　 B.外切　　 　　　　　C.内切　　　　　  D.相交

13.下列调查中适合用普查方法的是------------------------------------- （　 ）

A.要了解本班同学的身高　　　　　　　　　 B.要了解一批灯泡的使用寿命

C.要了解全国人口老龄化的情况　　　　　　 D.要了解电视台某娱乐节目的收视率

14.下列事件中，属于随机事件的是------------------------------------- （　 ）

A.掷一枚骰子所得点数不超过6　　　　　　  B.买彩票中奖

C.抛出的篮球会下落　　　　　　　　　　　 D.口袋中装有个红球，从中摸出一个白球

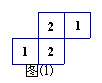
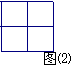
15. 如图⑴是几个小立方块所搭的几何体俯视图，小正方形中的数字表示该位置上小立方块的个数，则这个几何体的主视图是图⑵中的　　　　　　　　　　　　　　　 （　 ）

B

16．一艘轮船从A港出发，沿着北偏东65^o方向航行。行驶至B处，转向北偏西25^o方向航行。到达C处需要把航向恢复到出发时的航向，应如何调整航向　　　　　　　 （　 ）

A. 逆时针旋转90^o　　 B. 顺时针旋转90^o 　 C. 逆时针旋转40^oD. 顺时针旋转40^o

17．随着通讯市场竞争的日益激烈，某通讯公司的手机市话收费标准按原标准每分钟降低了

a元后，再次下调了25%，现在的收费标准是每分钟b元，则原收费标准每分钟为（　 ）

A．（）元　　　B．（）元　　 C．（元　　　D．（）元

18．如图，有一住宅小区呈三角形ABC形状，且周长为2000m，现规划沿小区周围铺上宽为3m的草坪，则草坪的面积（精确到1）是　　　　　　　　　　　　　　　  （　 ）

A. 6000㎡　　　　　  B. 6016㎡　　　　　 C. 6028㎡　　　　　  D. 6036㎡

第18题　　　　　　  第19题　　　　　　　　  第20题

19.如图⊿是⊿以点为中心逆时针旋转90°而得到的，其中＝1，

＝2，则弧的长为　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A .　　　　　　 B.　　　　　　  C.　　　　　　　  D.

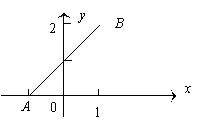
20．如图，已知点A（-1，0）和点B（1，2）在坐标轴上确定点P，使得ΔABP为直角三角形，则满足这样条件的点P共有　　　　　　　　　　　　　　　　　　　 （　 ）

A． 7个　　　　　　  B． 6个　　　　　  C． 4个　　　　　　　 D． 3个

三、认真答一答

21.计算：（1）；　　　（2）tan60°＋－3＋(6－π)⁰；

22．（1）解方程：　　  （2）解不等式组： 　 

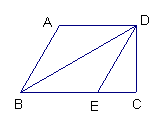
23．如图，在直角梯形ABCD中，AD//BC， DC⊥BC，E为BC边上的点，将直角梯形ABCD

沿对角线BD折叠，使△ABD△与EBD重合.若∠A=120°，AB=4，求EC的长.

24. 现有四块大小，质地均相同的卡片上分别写有“北”、“京”、“奥”、“运”。小明将四张卡片放入一个不透明的口袋中，让小芳从中随机抽出一张（不放回），再从口袋中剩下的3张中随机抽取第二张.

1）用列表或画树状图的方法，列出前后两次抽得的卡片上所写文字的所有可能情况.

2）若事先约定小芳抽得的两张卡片的文字能组成“北京”或“奥运”就可获得奖励，则小芳得到奖励的概率是多少？

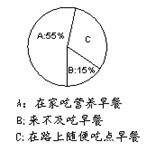25. 某校为了增加初三学生的复习时间，把上课时间提前到7:10；初二综合实践活动小组想探索这一举措的合理性，决定对初三学生到校时间及早餐质量进行调查。他们从早上6:30开始在校门口对初三到校学生进行观察统计，并把统计结果绘成条形统计图；然后对初三学生早餐质量进行抽样调查，并把结果画成扇形统计图.

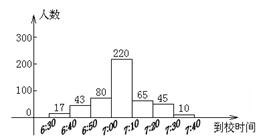
（1）该校初三学生约有　　　 人，迟到学生有　　  人，占初三学生总数的　　　%.

（2）计算因担心迟到而在路上随便吃点早餐的初三学生数.

（3）通过以上信息，你认为“初三提前到7:10上课”这一举措是否合理？为什么？

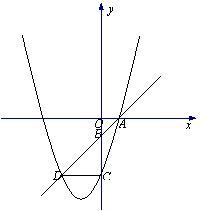
26．如图，一次函数y＝x＋m图象过点A（1，0），交y轴于点B，C为y轴负半轴上一点，且BC＝2OB，过A、C两点的抛物线交直线AB于点D，且CD∥x轴.

（1）求这条抛物线的解析式；

（2）观察图象，写出使一次函数值小于二次函数值时x的取值范围；

27.某电器商场今年在制定5月份A、B两种不同型号的彩电的进货方案时，由企划部提供如下信息：

型号	批发价（元/台）	物价局核 准零售价 （元/台）	厂方 现有量 （台）	5月份预计 销售量（台）	进货时 运费 （元/台）	商场可提供进货资金（元）	销售时商场需支付送货上门费用（元/台）
A	1500	1700	65	合计 100台	10	163000	15
B	1800	2100	55				20

　 设预计购进A型彩电x台，（假设进货量=预计销售量）

(1）根据上表信息，该商场有几种进货方案.

(2）试写出所获利润y（元）与x（台）之间的函数解析式；并说明何种方案预计获利最高？最高利润是多少？

四、动脑想一想

28.阅读下列材料并解决有关问题：我们知道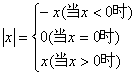：，现在我们可以用这一结论来解含有绝对值的方程.例如，解方程时，可令和，分别求得和，（称和分别为和的零点值），在实数范围内，零点值和可将全体实数分成不重复且不遗漏的如下3种情况：①　②　③，从而解方程可分以下三种情况：

① 当时，原方程可化为，解得.

② 当时，原方程可化为，解得，但不符合，故舍去.

③当时，原方程可化为，解得.

　综上所述，方程的解为，和.

　通过以上阅读，请你解决以下问题：

（1）、分别求出和的零点值.

（2）解方程

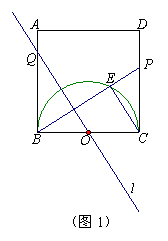29．已知正方形ABCD的边长为2，以BC边为直径作半圆O，P为DC上一动点（可与D重合但不与C重合），连结BP交半圆O于点E，过点O作直线l∥CE交AB（或AD）于点Q.

（1）如图1，求证：△OBQ∽△PEC.

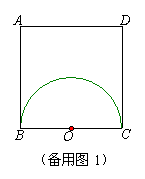（2）设DP＝t（0≤t＜2），直线l截正方形所得左侧部分图形的面积为S，试求S关于t的函数关系式.

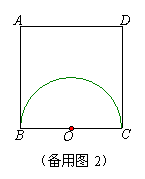
（3）当点Q落在AD（不含端点）上时，问以O、P、Q为顶点的三角形能否是等腰三角形？若能，请指出此时点P的位置；若不能，请说明理由.