2005年中考数学复习同步检测（39） （模拟题3） 姓名
2005届初中升学数学样卷（三）
一．填空题：（每小题3分，共30分）
1．计算：
；
2．纳米是一种长度单位．已知某种植物花粉的直径为36 000纳米，那么用科学记数法表示该花粉的直径为 纳米；
3．分解因式：
；
4．函数
的自变量
的取值范围是
；
5．若菱形的边长为1cm，其中一内角为60°，则它的面积为 ；
6．某食品店购进2000箱苹果，从中任取10箱，称得重量分别为（单位：千克）：16 16.5 14.5 13.5 15 16.5 15.5 14 14 14.5
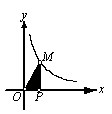若每千克苹果售价为2.8元，则利用样本平均数估计这批苹果的销售额是 元；
7．反比例函数
在第一象限内的图像如图，点M是图
像上一点，MP垂直轴于点P，如果△MOP的面积为1，那么k的值
是 ；
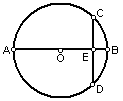8．已知抛物线
，当
时，
随的增大而减小，则的取值范围是 __；
9．如图，AB是⊙O的直径，弦CD⊥AB，E为垂足，若AB=9，
BE=1，则CD＝ ．
10．某工厂调整内部管理机制，计划两年后使成本降低
%，以适
应市场需求，若每年降低成本的百分数相同，设每年降低百分数为，则有方
程：_____ _____；
二．选择题：（每小题4分，共24分）
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
11。在
中，
，如果
，那么
的值等
（A） 
（B） 
（C） 
（D） 
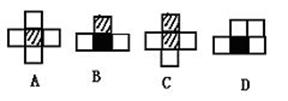
12．如下图中的四个正方形的边长均相等，其中阴影部分面积最大的图形是
13．如果用□表示1个立方体，用
表示两个立方体叠加，用■表示三个立方体叠加，那么下面右图由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是
 |
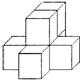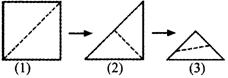
14．如图（1），小强拿一张正方形的纸，沿虚线对折一次得图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线剪去一个角，再打开后的形状是
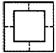
（A） （B） （C） （D）
15．如果圆柱的母线长为5cm，底面半径为2cm，那么这个圆柱的侧面积是
（A） 
（B） 
（C） 
（D）
16．一班学生检查视力，
结果如左图：
从上述数据上看出，全班视力数据的众数是
（A） 0.9 （B） 1.0 （C） 20％ （D） 65％
三．解答题：
17．（7分）计算：
18．（8分）先化简．再求值：
，其中
；
19．（8分）我省某城镇邮政局对甲、乙两个支局的报刊发行部2002年度报纸的发行量进行了统计，并绘成统计图如下：
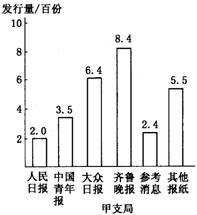
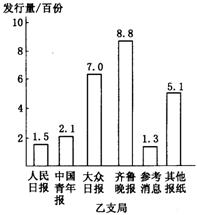
请根据上面统计图反映的信息，回答问题：
⑴ 哪个支局发行《齐鲁晚报》的份数多？多多少？
⑵ 分别写出上面两个统计图中提供的6个统计数据的中位数；
⑶ 巳知甲、乙两个支局所服务的居民区住户分别是11280户、8600户，哪个居民区平均每户订阅报纸的份数多？试说明理由．
20．（9分）某电脑软件经销店，以每件30元的进价购进一种新开发的软件W,通常销售利润可达到进价的60%.为促进商店内与软件W相关联的其它软件(销售价格不变)的销售，决定将软件W在不赔本的情况下,每件的销售利润以不高于进价30%的可变价格出售，用来招揽顾客.经过几天销售发现，其它软件日均销售利润元与软件W的售价x元满足一次函数关系，当软件W的售价分别是33元和38元时，其它软件的销售利润分别是188元和168元.
（1）
求出y与x的函数关系式，并写出的取值范围；
（2） 若在一天中，能将19件软件W售出，销售软件W与销售其他软件的利润和不低于230元，试确定软件W的售价范围.（利润＝售价—进价）
21．（10分）如图，在矩形 ABCD中，F是BC边上一点，AF的延长线交DC的延长线于G，DE⊥AG于E，且DE＝DC．根据上述条件，请在图中找出一对全等三角形，并证明你的结论．
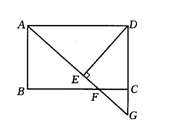
22．（12分）如图，Rt⊿ABO的顶点A是双曲线
与直线
在第二象限的交点，AB⊥轴于B，且
（1） 求这两个函数的解析式；
（2） 求直线与双曲线的两交点A、C的坐标和⊿AOC的面积；
y
A
O
x
B C
23. （9分）如图：何新家居住的甲楼AB面向正北，现计划在他家居住的楼前修一座乙楼CD，楼高约为
，两楼之间的距离为
，已知冬天的太阳最低时，光线与水平线的夹角为
；
（1）试求乙楼CD的影子落在甲楼AB上高BE的长；
（2）若让乙楼的影子刚好不影响甲楼，则两楼之间的距离至少应是多少？（精确到
）
（参考数据：
，
，
，
）
24．（12分）如图，⊙O1与⊙O2外切于点P，外公切线AB切⊙O1于点A，切⊙O2于点B，
（1）求证： AP⊥BP；
（2）若⊙O1与⊙O2的半径分别为
和
，求证：
；
（3）延长AP交⊙O2于C，连结BC，若
，求
的值；
 |
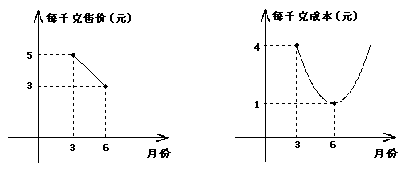
25．（12分）某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，在对历年市场行销和生产情况进行了调查的基础上，对今年这种蔬菜上市后的市场售价和生产成本进行了预测，提供了两方面的信息（如甲、乙两图）注：甲、乙两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本，生产成本月份最低；甲图的图象是线段，乙图的图象是抛物线.请根据图象提供的信息说明，解决下列问题：⑴在3月份出售这种蔬菜，每千克的收益是多少？⑵哪个月出售这种蔬菜，每千克的收益最大？说明理由.（收益=售价-成本）
 |
26．（9分）如图，
是⊙O的直径，
是⊙O上的一点，直线
交的延长线于点
，
于
，且
(1) 求证：
是⊙O的切线
(2) 若⊙O的半径为
，
.求
的长.
 |
2005届初中升学数学样卷（三）答案
一．填空题：
1．
；
2．
；
3．
；
4．
；
5．
6．
；
7．；
8．
；
9．
；
10．
二．选择题：
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | B | B | B | C | D | B |
17．原式
；
18化简得：
，
；
19．乙支局多，多
万份，
，甲25份，乙30份；
20．（9分）某电脑软件经销店，以每件30元的进价购进一种新开发的软件W,通常销售利润可达到进价的60%.为促进商店内与软件W相关联的其它软件(销售价格不变)的销售，决定将软件W在不赔本的情况下,每件的销售利润以不高于进价30%的可变价格出售，用来招揽顾客.经过几天销售发现，其它软件日均销售利润元与软件W的售价x元满足一次函数关系，当软件W的售价分别是33元和38元时，其它软件的销售利润分别是188元和168元.
（3） 求出y与x的函数关系式，并写出的取值范围；
（4） 若在一天中，能将19件软件W售出，销售软件W与销售其他软件的利润和不低于230元，试确定软件W的售价范围.（利润＝售价—进价）
设其它软件日均销售利润元与软件W的售价x元的函数关系为y=kx+b（2分）
由题意得：
解得：k=－4，b=320…………………………………………………5分
∴y=－4x+320…………………………………………………………6分
(2)由题意得：19（x－30）+(－4x+320)≥230
解得：x≥32…………………………………………………………9分
又∵x≤30(1+30%)=39………………………………………………11分
∴32≤x≤39…………………………………………………………12分
21．⊿ABF≌⊿ADE。（AAB）
22．（1）
，
；
（2）A
，
，C
，
，
；
23．（1）过点E作EG∥FD交CD于点G，则有：
在Rt⊿CGE中
∵∠CEG =
∴CG =
∴
答：乙楼CD的影子落在甲楼AB上高BE的长是
。（不答扣1分）
（2）在Rt⊿CFD中
答：两楼之间的距离至少应是
。（不答扣1分）
；
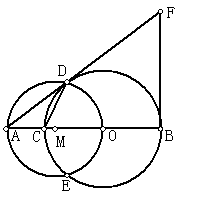
24．（1）作公切线
如图，C为线段AB上一点，以BC为直径作⊙O,再以AO为直径作⊙M交⊙O于D、E，过点B作AB的垂线交AD的延长线于F，连结CD。
（1）若AC＝2，且AC与AD的长是关于的方程
的两个根。①求证：AD是⊙O的切线；②求线段DF的长；③求sin∠ADC的值。（2）当点C是线段AB上的一动点（点A、B除外），
为何值时，△ACD是等腰三角形。
