2005年中考数学复习同步检测（40） （模拟题4）　　 　姓名　　　　 

2005届初中升学数学样卷（四）

一．填空题：（每小题3分，共30分）

1.　的倒数是 = 　　　　　　；

2．今年我市参加中考的考生预计约将达到人,这个数字用科学记数法并保留两位有效数字表示为　　　　　　　　　 人；

3．分解因式：；

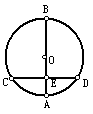4．如果梯形的中位线长为9cm，下底的长为12cm，那么这个梯形的上底长等于　 　　 cm；

5．如图，AB是⊙O的直径，弦，垂足为E，如果AB=10，CD=8，

那么AE的长为　　　　　　  ；

6．一个面积为144的正方形中，阴影部分中的小直角三角形的斜边长

是　　　　　  ；

7．抛物线的顶点坐标是　　　　　　 ；

对称轴是　　 　　　　 ；

8．以三角形的三个顶点为顶点的平行四边形可以作

　　　　　　　　  个；

9．甲、乙两班举行电脑汉字输入速度比赛，参加学生每分钟输入汉字的个数经统计计算后填入下表：

班级	参加人数	中位数	方差	平均字数
甲	55	149	191	135
乙	55	151	110	135

某同学根据上表分析得出如下结论：①甲、乙两班学生成绩的平均水平相同；②乙班优秀的人数多于甲班优秀的人数（每分钟输入汉字数≥150个为优秀）；③甲班成绩的波动情况比乙班的波动大。上述结论正确的是 　　　　　　　　 ；

10．国家对电信资费进行了调整，区内（主城区或县内）的收费标准是月租费25元，首次3分钟0.2元（不足3分钟按3分钟计），以后每分钟0.1元（不足1分钟计为1分钟），若本月该用户区内电话累计通话100分钟，共通话30次，问他本月至少要缴纳区内话费　　　　元；

二. 选择题（每小题4分，共24分）

题号	11	12	13	14	15	16
答案

11. 计算：的结果是

（A）　　 　　 （B）　　 　　 （C）　　　　 （D）　 以上答案都不对

12. 河水的平均深度为2.5米，一个身高1.5米但不会游泳的人下水后肯定会

(A)　 肯定会淹死　 (B)　 不一定会淹死　　(C)　　淹不死　　 (D)　　以上答案都不对

13. 下列各图经过折叠不能围成一个正方体的是　　　

　　　　　　　  　　　　　　　　　　　

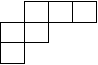
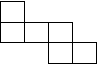
（A）　　　　　　　  （B）　　　　　　 　（C）　　　　　　 （D）

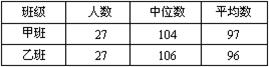14. 为了解我市初三女生的体能状况，从某校

初三的甲、乙两班中各抽取27名女生进行一

分钟跳绳次数测试，测试数据统计结果如右表。

如果每分钟跳绳次数≥105次的为优秀，那么甲、乙两班的优秀率的关系是

 (A)　　 甲_优＜乙_优　　　　(B)　　甲_优＞乙_优　 (C)　　 甲_优＝乙_优 　 (D)　　无法比较

15. 对于二次函数为，当自变量时，函数图像在

(A)　 第一、二象限　　　(B)　 第二、三象限　(C)　 第三、四象限  (D)　 第一、四象限

16．在直角坐标系中，横、纵坐标都是整数的点称为整点，那么一次函数在一象限的图象上，整点的个数是

(A)　　　2个　　 　(B)　　　3 个　　　(C)　　　4 个　　　(D)　　 6个

三.解答题：

17. （7分）计算：

.

18. （8分）先化简，再求值： ，其中

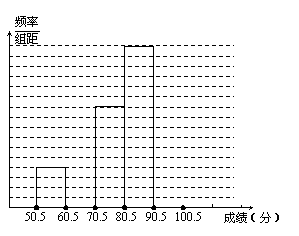
19. （9分）为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：

（1）填充频率分布表中的空格；

（2）补全频率分布直方图；

（3）在该问题中的样本容量是多少？

　　　 答：　　　　　　　　　　　　　．

（4）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由）

　　　 答：　　　　　　　　　　　　　．

（5）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？

频率分布直方图

　　　 答：　　　　　　　　　　　　　．

频率分布表
分组	频数	频率
50.5～60.5	4	0.08
60.5～70.5	8	0.16
70.5～80.5	10	0.20
80.5～90.5	16	0.32
90.5～100.5
合计

20．（8分）某车间有工人 20多名，每人每天加工甲种零件5个或乙种零件4个，在20名工人中，派人加工甲种零件，其余的加工乙种零件，已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元，

（1）　　　 写出车间每天所获利润元与人之间的函数关系式；

（2）　　　 若要使车间每天获利不低于1800元，问至少要派多少人加工乙种零件？

21．（10分）菱形的一个角顶点到与它不相邻的两边的距离会相等吗？若相等，证明出来；若不相等，请说明理由。

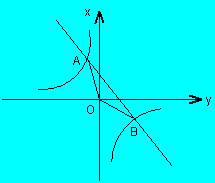
22． （12分）如图，已知一次函数的图象与反比例函数的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是，求：

（1）一次函数的解折式；

（2）△AOB的面积。

23．（9分）在开发区建设中，要拆除烟囱，在地面上事先画定以为圆心，半径与等长的圆形危险区，现在从离点米远的建筑物顶点，测得点的仰角为，点的俯角为，问离点米远的文物保护区是否在危险区内，请通过计算说明。

24. （12分）如图，BC是⊙O的直径，A是弦BD延长线上一点，切线DE平分AC于E。 （1）求证：AC是⊙O的切线；

（2）若AD∶DB=3∶2，AC=15，求⊙O的直径；

（3）求的值；

25. （12分）已知：如图，⊙O和⊙O相交于A、B两点， ⊙O经过点O，点C在A OB上运动（点C不与A、B重合），AC的延长线交⊙O于P，连结AB、BC、BP；

（1）按题意将图形补充完整；

（2）当点C在A OB上运动时，图中不变的角有　　　　　　　　　　　　　　　 （将符合要求的角都写上）

（3）线段BC、PC的长度存在何种关系？写出结论，并加以证明；

（4）设⊙O和⊙O的半径为、，当，满足什么条件时，为等腰直角三角形？

26. （10分）某商场经营一批进价为元的小商品，在市场营销中发现日销售单价元与日销售量件有如下关系：

	3	5	9	11
	18	14	6	2

（1）预测此商品日销售单价为11.5元时的日销售量；

（2）设经营此商品日销售利润（不考虑其他因素）为元，根据销售规律，试求日销售利润元与销售单价元之间的函数关系式，问日销售利润是否存在最大值或最小值？若有，试求出；若无，请说明理由；

2004届初中升学数学样卷（八）　　答案

一．填空题：

1．； 2．； 3．； 4．； 5．； 6．；

7．，，； 8．； 9．（1）（2）（3）； 10．；

二．选择题：

题号	11	12	13	14	15	16
答案	B	D	D	A	B	A

三．解答题：

17．原式

18．原式，化简的；

19．样本容量为；的参赛人数最多。表格：，；

20．（1）

（2）要使≥，即≥，∴≤，

∴，∴派往乙种零件的人数至少要人。

21．略

22．（1）；（2）；

23．∵，不在危险区内。

24．（1）连结OE，由中位线证平行，证⊿EDO≌⊿ECO；（2）由，得出AB的长，再用勾股定理求⊙O的直径为；（3）；

25．（1）作图；（2）∠ACB，∠BCP，∠APB，∠CBP；（3）连结AO、BO，

∵∠AOB =∠ACB = 2∠P，∠ACB = ∠CBP +∠P，∴∠CBP =∠P，∴CB = CP；

（4）要使⊿BCP为等腰直角三角形，已有CB = CP，只需∠BCP =，只需弦AB为直径，C点与O重合，∴，∴是必须满足的条件。

26．设销售单价（元）与日销售量（件）的关系式为：，根据题意得：

，∴所求函数关系式为：

当元时：

（2）∵小商品的进价为2元，利润与进价、件数之间的关系有：

∴当或时，P有最小值

当时，P有最大值；