《相似图形》中考热点透视
一、探索条件型
例1(2004陕西)如图1,矩形ABCD,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系一定满足( D )
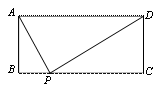
图1
A. a≥![]() b; B.a≥b; C. a≥
b; B.a≥b; C. a≥![]() b; D.a≥2b.
b; D.a≥2b.
分析:由于矩形是轴对称图形,根据其对称性可知,通常情况下点P的位置有两个,它们关于BC的垂直平分线对称;如果存在一点P,则该点必为BC的中点,此时△ABP≌△DCP,则AP=DP,△APD为等腰直角三角形。要使△ABP、△APD、△CDP两两相似,则它们都是等腰直角三角形。
此时,![]() ,即a=2b。
,即a=2b。
当点P的位置有两个时,a>2b。
总之,a≥2b。故选D.
例2(2004浙江宁波)如图2,已知点![]() 是边长为4的正方形
是边长为4的正方形![]() 内一点,且
内一点,且![]() ,
,![]() ,垂足是
,垂足是![]() .请在射线
.请在射线![]() 上找一点
上找一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似(请注意:全等图形是相似图形的特例)
.
相似(请注意:全等图形是相似图形的特例)
.

图2
分析:由于对应点没有确定,所以需分类讨论。
(1)若△MBC∽![]() ,则需在射线
,则需在射线![]() 上截取线段
上截取线段![]() ,连结
,连结![]() ,
,
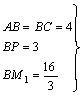
![]()
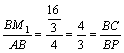 ,
,
![]()
![]()
![]() ,
,
∴![]() ~
~![]() .
.
(2)若△CBM∽![]() ,则需在射线
,则需在射线![]() 上截取线段
上截取线段![]() ,连结
,连结![]() ,
,
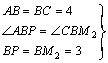
![]()
![]() .(全等必相似)
.(全等必相似)
∴在射线![]() 上取
上取![]() 或
或![]() 时,
时,![]() ,
,![]() 都为符合条件的
都为符合条件的![]() .
.
二、探索结论型
例3(2004江苏淮安)已知:如图3,在□ABCD中,点E为边CD上的一点,AE的延长线交BC的延长线于点F,请你写出图中的一对相似三角形:△______∽△_________.(只使用图中已有字母,不再添加辅助线)
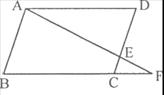
图3
分析:本题有多种答案。注意到AD//CF,则△EDA∽△ECF;注意到CE//BA,则△ABF∽△ECF;利用相似形之间的“传递性”,有△ABF∽△EDA。
例4(2004四川资阳)如图4①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3 .
(1) 如图4②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(不必证明)
(2) 如图4③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明;
(3) 若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1、S2、S3表示,为使S1、S2、S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件?证明你的结论;
(4) 类比(1)、(2)、(3)的结论,请你总结出一个更具一般意义的结论 .
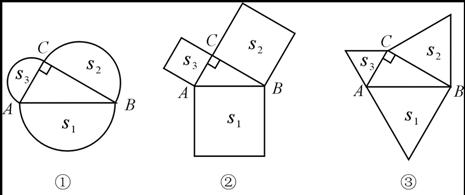
图4
分析:设直角三角形ABC的三边BC、CA、AB的长分别为a、b、c,则c2=a2+b2 .
(1) S1=S2+S3 .
(2) S1=S2+S3 . 证明如下:
∵ 所作三个正方形相似,∴ ![]()
![]() .
.
(3) 当所作的三个三角形相似时,S1=S2+S3 . 证明如下:
∵ 所作三个三角形相似, ∴ ![]()
![]() .
.
(4)由于半圆、正方形、等边三角形都是相似图形,所以类比(1)、(2)、(3)的结论,可得:
分别以直角三角形ABC三边为一边向外作相似图形,其面积分别用S1、S2、S3表示,则S1=S2+S3 .
三、猜想规律型
例5(江苏连云港)如图5,在梯形ABCD中,AB∥CD,![]() ,
,![]() ,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
①当![]() 时,有
时,有![]() ;
;
②当![]() 时,有
时,有![]() ;
;
③当![]() 时,有
时,有![]() .
.
当![]() 时,参照上述研究结论,请你猜想用k表示DE的一般结论,并给出证明。
时,参照上述研究结论,请你猜想用k表示DE的一般结论,并给出证明。
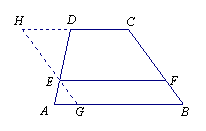
图5
分析:类比条件中的等式,可以猜想得:EF =![]() .
.
证明:过点E作BC的平行线交AB于G,交CD的延长线于H.
∵AB∥CD,∴![]() ∽
∽![]() ,∴
,∴![]() ,
,
又![]() ∥
∥![]() ∥
∥![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,可得
,可得![]() .
.
四、阅读理解型
例6(2004江苏南京)如果两个三角形不仅是相似三角形,而且每对对应点所在的直线都经过同一个点,那么这两个三角形叫做位似三角形,它们的相似比又称为位似比,这个点叫做位似中心.利用三角形的位似可以将一个三角形缩小或放大.
(1)选择:如图6-1,点O是等边三角形PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形.此时,△P′Q′R′与△PQR的位似比、位似中心分别为( ).
A.2、点P B.![]() 、点P C.2、点O D.
、点P C.2、点O D.![]() 、点O
、点O


图6-1 图6-2
(2) 如图6-2,用下面的方法可以画△AOB的内接等边三角形.阅读后证明相应问题.
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;
②连结OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,
作E′D′∥ED,交OB于点D′;
③连结C′D′.则△C′D′E′是△AOB的内接三角形.
求证:△C′D′E′是等边三角形.
分析:(1)△P′Q′R′与△PQR的位似比即为其相似比![]() ;对应点所在的直线PP’、’、RR’都经过点O,所以,位似中心为点O。故选D.
;对应点所在的直线PP’、’、RR’都经过点O,所以,位似中心为点O。故选D.
(2)∵E′C′∥EC,∴△C’E’O∽△CEO,∴∠C’E’O=∠CEO,![]() 。
。
∵E′D′∥ED,∴△D’E’O∽△DEO,∴∠D’E’O=∠DEO, ![]()
∴∠C’E’ D’ =∠CED,![]() ,∴△CDE∽△C′D′E′。
,∴△CDE∽△C′D′E′。
由于△CDE为等边三角形,所以△C′D′E′也是等边三角形.
五、实际应用型
例7(2003山东济南)检查视力时,规定人与视力表之间的距离应为5米,如图7(1).现因房间两面墙的距离为3米,因此使用平面镜来解决房间小的问题,若使墙面镜子能呈现完整的视力表,如图7(2).由平面镜成像原理,作出了光路图,其中视力表AB的上下边沿A、B发出的光线经平面镜MM’的上下边沿反射后射入人眼C处.如果视力表的全长为O.8米,请计算出镜长至少为多少米?


图7
分析:相似形在实践中,尤其在测量等方面,有着广泛的应用。本题即为一例。
作CD⊥MM’,垂足为D,延长CD交A'B'于点E.
∵AB′∥MM’//A’B’,∴CE⊥A’B’,△CMM’∽△CAB’,
∴![]() .
.
∵CD = 5 – 3 =2 , CE = 5 , A’B’= AB = 0.8,
∴![]() .
.
∴MM’=0.32(米).
∴镜长至少为0.32米.