2005年中考数学复习同步检测（17）　　　　　　  姓名　　　　 

（三角形1）

一．填空题：

1．在中，与∠B相邻的外角等于140°，则∠A +∠C＝　　　　  度；

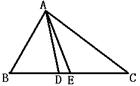2．如图：AD、AE分别是的角平分线和中线，如果

∠BAD＝50°，CE＝5cm，那么∠BAC=　　　　　 度，

BC＝　　　　　 cm；

3．等腰三角形的两条边长分别为10cm和5cm，它们的周长是　　　　 cm；

4．如图1，图中共有　　　　 个三角形，其中以AB为一边的三角形

有　　　　　　　 ，以为一个内角的三角形

有　　　　　　　　　　 。

5．如图2，在中，已知AE是中线，AD是角平分线，AF是高，根据已知条件填空：

（1）BE=　　　　　 =　　　　；

（2）=　　　　 =　　　　 ；

（3）　　　　=

6．两根木棒的长分别是7cm和10cm，要选择第三根木棒，将它们盯成三角形，第三根木棒长的范围是　　　　　　 ；

7．判断具备下面条件的三角形是直角三角形、锐角三角形还是钝角三角形：

（1）如果，那么是　　　　 三角形；

（2）如果，，那么是　　　　  三角形；

（3）如果，那么是　　　　  三角形。

8．如图3所示，，

则　　　　　　 ，=　　　　　 。

9．中，AD是的中线，且，则BD=　　　　 cm；

10．在中，，AD为的平分线，则=　　　　度；

11．三角形三边为3，5 ，则的范围是　　　　　  　　　；

12．三角形两边长分别为25cm和10cm，第三条边与其中一边的长相等，则第三边长为　　　　  　　；

13．等腰三角形的周长为14，其中一边长为3，则腰长为　　　　　　；

14．一个三角形周长为27cm，三边长比为2∶3∶4，则最长边比最短边长　　　　。
15。等腰三角形两边为5cm和12cm，则周长为　　　　　　；

16．已知：等腰三角形的底边长为6cm，那么其腰长的范围是　　　　　　 ；

二．选择题：　

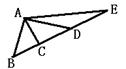
17．如图，共有三角形的个数是　　　　　　　　　　　　　　　　　　　　　　  （　　）

A．　　　3　　　　B．　　　4　　　　C．　　　 5　　　　D．　　 6

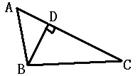18．如图，AB⊥BC，垂足为B；BD⊥AC，垂足为D，图中共有直角三角形　　　 （　　）

A　　 2个　　B　　 3个　　 C　　　4个　　D　　5个

19．三角形只有一条高在三角形内，另两条高在三角形边上，

这个三角形一定是　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A　　锐角三角形　　B　　直角三角形　　C　　钝角三角形　　D　 任意三角形

20．以下列长度（cm）的三条小木棒，如果首尾顺次连洁，能钉成三角形的是　　 （　　）

A　 10、14、24　　 B　　12、16、32　　C　　 16、6、4　　 D　　8、10、12

21．一个三角形的内角中，至少有一个角的度数不会大于　　　　　　　　　　　  （　　）

A　　　 60°　　　 B　　　　90°　　　C　　　 120°　　　D　　 150°

22．以下长度为边的三条线段能组成三角形的组数是　　　　　　　　　　　　　  （　　）

① 1，2，3 ；② 2，3，4　；③ 4，5，6 ；④ 5，6，10；

A　　　一组　　　 B　　　两组　　　  C　　　　三组　　　 D　　　四组

23．已知三角形的三边分别为2，，4那么的取值范围是　　　　　　　　　　 （　　）

A　　　　B　　 　　C　　　 　　D　　

24．如图，于D，于E，于F，于A，则 中，AC边上的高为　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　（　　）

A　　 AD　　B　　 GA　　 C　　 BE　　 D　 CF

25．在一个三角形，若，则是　　　　　　　　　　　　  （　　）

A　　直角三角形　 B　　锐角三角形　　C　　 钝角三角形　　D　　 以上都不对

27．三角形的高线是　　　　　　　　　　　　　　　　　　 　　　　　　　　　（　　）

A　　  直线　　　 B　　　 垂线　　　 C　　　 射线　　　  D　　直线

28．如果一个三角形的三条高线的交点恰好是三角形的一个顶点，那么这个三角形是　（　　）

A　　直角三角形　 B　　锐角三角形　　C　　 钝角三角形　　D　　不能确定

29．在下图中，正确画出AC边上高的是　　　　　　　　　　　　　　　　　　　 （　　）

A　 　　　　　B　　　　　　　 C　　　　　　　  D

30．等腰三角形的周长为16，且边长为整数，则腰与底边分别为　　　　　　　　  （　　）

A　　　 5，6　　 B　　　6，4　　 　C　　　 7，2　　　D　　以上三种情况都有可能

31．一个三角形两边分别为3和7，第三边为偶数，第三边长为　　　　　　　　　 （　　）
A　　　 4，6　　 B　　 4，6，8　　 C　　　 6，8　　　D 　 6，8，10

32．已知三角形的一个外角小于与它相邻的内角，那么这个三角形　　　　　　　　 （　　）

A、是锐角三角形　B、是直角三角形　　C、是钝角三角形　D、以上三种都有可能

三．解答题：

33．已知等腰三角形的两边长分别为11cm和5cm，求它的周长；

34．已知等腰三角形的底边长为8cm，一腰的中线把三角形的周长分为两部分，其中一部分比另一部分长2cm，求这个三角形的腰长；

35．已知等腰三角形一边长为24cm，腰长是底边的2倍，求这个三角形的周长。

36．沿虚线，画出四种不同的方案，分别将下面的四个正方形划分成两个全等的图形．

37．初一(1)班的篮球拉拉队同学，为了在明天的比赛中给同学加油助威，提前每人制作了一面同一规格的三角形彩旗．小明放学回家后，发现自己的彩旗破损了一角，他想用彩纸重新制作一面彩旗．请你帮助小明，用直尺与圆规在彩纸上作出一个与破损前完全一样的三角形．

38．（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A＝30°，则∠ABC＋∠ACB＝　　　　　　 度，∠XBC＋∠XCB＝　　　　　  度；

（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C，那么∠ABX＋∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX＋∠ACX的大小．

图1　　　　　　　　　　　　　　 图2