2005年中考数学复习同步检测（34） （新型题1） 姓名
一．选择题：
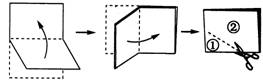
1． 将一张矩形纸对折再对折（如图），
然后沿着图中的虚线剪下，得到①、②
两部分，将①展开后得到的平面图形是 （ ）
A． 矩形 B． 三角形 C． 梯形 D． 菱形
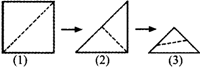2．如图⑴，小强拿一张正方形的纸，沿虚线对折一次得图⑵，再对折一次得图⑶，然后用剪刀沿图⑶中的虚线剪去一个角，再打开后的形状是 （ ）
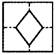
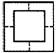
A. B. C. D.
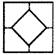
3．下面的图形都是由6个大小一样的正方形拼接而成的，这些图形中可折成正方体的是 （ ）
4．右图是正方体分割后的一部分，它的另一部分为下列图形中的 （ ）
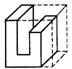
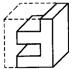
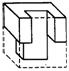
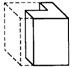
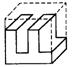
A. B. C. D.
5．如图，观察下列用纸折叠成的图案
其中，轴对称图形和中心对称图形的个数分别为 （ ）
A. 4、1 B. 3、1 C. 2、2 D. 1、3
6．在平行四边形ABCD中，AB＝6，AD＝8，∠B为锐角，将△ACD沿对角线AC折叠点D落在△ABC所在平面内的E处.如果AE过BC的中点，则平行四边形ABCD的面积是（ ）
A. 24 B. 2
C. 10
D. 24
7．一块等边三角形的木板，边长为1，现将木板沿
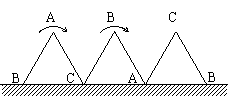水平线翻滚（如图），那么B点从开始至结束所走
过的路径长度为 （ ）
A. 
B. 
C. 4 D. 2＋
8．张师傅下岗再就业，做起了小商品生意，第一次进货时，他以每件
元的价格购进了20件甲种小商品，每件
元的价格购进了30件乙种小商品（
）；回来后，根据市场行情，他将这两种小商品都以每件
元的价格出售，在这次买卖中，张师傅是
（ ）
A 赚钱 B 赔钱 C 不赚不赔 D 无法确定赚和赔
9．如果用□表示1个立方体，用 表示两个立方体叠加，用■表示三个立方体叠加，那么下面右图由6个立方体叠成的几何体，从正前方观察，可画出的平面图形是
A B C D
二．填空题：
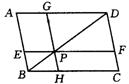
10．如图，在平行四边形ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上
图中有 对四边形面积相等；
它们是
；
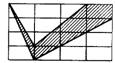
11．如图是阳光广告公司为某种商品设计的商标图案，
图中阴影部分为红色.若每个小长方形的面积都1，则红色的面积是 ；
12．写出一条经过第一、二、四象限，且过点(
，
)的直线解析式
；
13．某种商品的进价为800元，出售时的标价为1200元，后来由于该商品积压，商店准备打折出售，但要保持利润率不低于5%，则至少可打 折；
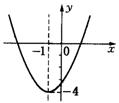
14．二次函数
的图象如图所示，则函数值
时，对应
的取值范围是
；
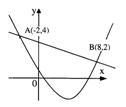
15．已知二次函数
（
）与一次函数
的图象相交于点A （－2，4），B（8，2）（如图所示），则能使
成立的的取
值范围是_______ __；
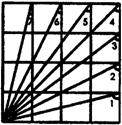
16．在如图所示的
正方形网格中．
∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝
；
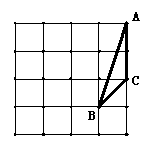
17．以图中的格点为顶点，画一个与已知△ABC相似的
三角形(相似比不为1).
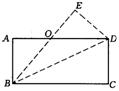
18．已知：如图，把一张矩形纸片ABCD沿BD对
折，使C点落在E处，BE与AD相交于点O．写出
二组相等的线段（不包括AB＝CD和AD＝BC）．
.
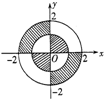
19．如图，是以直角坐标原点O为圆心的两个同心圆，则其阴影部分
的面积之和 ；(结果保留π)
20．用两块完全重合的等腰直角三角形纸片拼下列图形：
⑴平行四边形(不包括矩形、菱形、正方形)；
⑵矩形；⑶正方形；⑷等边三角形；⑸等腰直角三角形，
一定能拼成的图形是 .(填序号
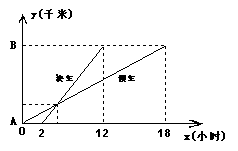21．一慢车和一快车沿相同路线从A地到相距120千米的B地，
所行地路程与时间的函数图像如图所示.试根据图像，回答下列
问题: ⑴慢车比快车早出发 小时，快车比慢车少用
小时到达B地；⑵快车用 小时追上慢车；
此时相距A地 千米.
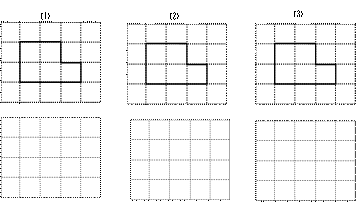
22.现有一块形如母子正方形的板材，木工师傅想先把它分割成几块，然后适当拼接，制成某种特殊形状的板面（要求板材不能有剩余，拼接时不重叠、无空隙），请你按下列要求，帮助木工师傅分别设计一种方案：
⑴板面形状为非正方形的中心对称图形；⑵板面形状为等腰梯形；⑶板面形状为正方形.
请在方格纸中的图形上画出分割线，在相应的下边的方格纸上面拼接后的图形.
23.⑴四年一度的国际数学家大会于2002年8月20日在北京召开．大会会标如图甲．它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积为13，每个直角三角形两直角边的和是5．求中间小正方形的面积．
⑵现有一张长为6.5cm、宽为2cm的纸片，如图，请你将它分割成6块，再拼合成一个正方形．（要求：先在图乙中画出分割线，再画出拼成的正方形并标明相应数据）
24．在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌）．这显然与正多边形的内角大小有关．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．
⑴请根据下列图形，填写表中空格：
| 正多边形边数 | 3 | 4 | 5 | 6 | … | n |
| 正多边形每个内角的度数 | 60° | 90° | 108° | 120° | … |
|
⑵如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形?
⑶从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由．
25．取一张矩形的纸片进行折叠，具体操作过程如下：
第一步：先把矩形ABCD对折，折痕为MN，如图（1）；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B`，得Rt△AB`E，如图（2）；
第三步：沿EB`线折叠得折痕EF，如图（3）.
利用展开图（4）探究：
⑴△AEF是什么三角形？
⑵对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由.
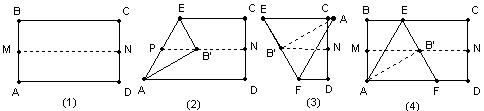
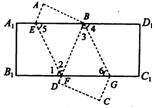
26．如图，矩形A1BlC1D1沿EF折叠，使B1点落在A1D1边上的B处；沿BG折叠，使D1点落在D处且BD过F点.
(1)求证：四边形BEFG是平行四边形；
(2)连结B1B；判断△B1BG的形状，并写出判断过程．
