梅州市2005年中考数学模拟试题(二)
班级: 姓名: 座号: 评分:
一、填空题(每小题3分,共30分)
1.—(—5)=
;—3=
;![]() =
。
=
。
2.在函数![]() 中,自变量
中,自变量![]() 的取值范围是
。
的取值范围是
。
3.若∠α的余角是30°,则∠α= °,sinα= 。
4.太空探测器“先驱者10号”从发射到2003年2月人们收到它最后一次发回的信号时,它已飞离地球km,用科学记数法表示这个距离为 km。
5.点A(﹣1,2)关于![]() 轴的对称点坐标是
;点A关于原点的对称点的坐标是
。
轴的对称点坐标是
;点A关于原点的对称点的坐标是
。
6.已知一元二次方程![]() 的两个根是
的两个根是![]() 、
、![]() ,则
,则![]() = ,
= ,
![]() =
,
=
,![]() =
。
=
。
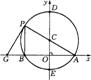
 7.如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
cm, ∠ABD=
°。
7.如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
cm, ∠ABD=
°。
8.有两块同样大小且含角60°的三角板,把它们相等的边拼在一起(两块三角板不重叠),可以拼出 个四边形。
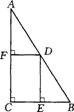 9.如图,点D是Rt△ABC的斜边AB上的一点,DE⊥BC于E,DF⊥AC于F,若AF=15,BE=10,则四边形DECF的面积是
。
9.如图,点D是Rt△ABC的斜边AB上的一点,DE⊥BC于E,DF⊥AC于F,若AF=15,BE=10,则四边形DECF的面积是
。
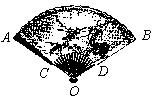
10.如图,一扇形纸扇完全打开后,两竹条外侧OA和OB的夹角为120°,OC长为8cm,贴纸部分的CA长为15cm,则贴纸部分的面积为 cm2(结果保留π)
二、选择题(每小题3分,共15分)
11.下列命题中错误的命题是 ( )
(A)![]() 的平方根是
的平方根是![]() (B)平行四边形是中心对称图形
(B)平行四边形是中心对称图形
(C)单项式![]() 与
与![]() 是同类项(D)近似数
是同类项(D)近似数![]() 有三个有效数字
有三个有效数字
12.下列图形中既是轴对称图形又是中心对称图形的是

A B C D
13.如果圆柱的底面半径为4cm,母线长为5cm,那么它的侧面积等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14.关于![]() 的一元二次方程
的一元二次方程![]() 根的情况是 ( )
根的情况是 ( )
(A)有两个不相等实数根 (B)有两个相等实数根
(C)没有实数根 (D)根的情况无法判定
15. 关于函数![]() ,下列结论正确的是
( )
,下列结论正确的是
( )
(A)图象必经过点(﹣2,1) (B)图象经过第一、二、三象限
(C)当![]() 时,
时,![]() (D)
(D)![]() 随
随![]() 的增大而增大
的增大而增大
三、解答题(每小题6分,共24分)
16.
不用计算器计算:![]() ÷(—2)2 —2 -1+
÷(—2)2 —2 -1+![]()
17.已知x=![]() +1,求代数式
+1,求代数式![]() 的值
的值
18.解方程:![]() 。
。
19.已知一个二次函数的图象经过点(0,0),(1,﹣3),(2,﹣8)。
(1)求这个二次函数的解析式;
(2)写出它的对称轴和顶点坐标。
四、(20、21小题各7分,22、23小题各8分,共30分)
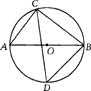
 20.如图,点A、B、C、D在⊙O上,AB=AC,AD交BC于点E,AE=2,ED=4,求AB的长。
20.如图,点A、B、C、D在⊙O上,AB=AC,AD交BC于点E,AE=2,ED=4,求AB的长。
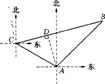
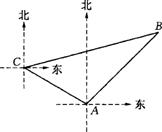 21.如图,甲、乙两只捕捞船同时从A港出海捕鱼。甲船以每小时
21.如图,甲、乙两只捕捞船同时从A港出海捕鱼。甲船以每小时![]() 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进。甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇。
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进。甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇。
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
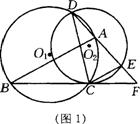
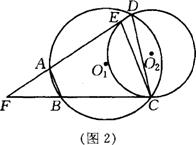
22.如图,⊙O2与⊙O1 的弦BC切于C点,两圆的另一个交点为D,动点A在⊙O1,直线AD与⊙O2交于点E,与直线BC交于点 F 。
(1)如图1,当A在弧CD上时,求证:
①⊿FDC∽⊿FCE;
② AB∥EC ;
(2)如图2,当A在弧BD上时,是否仍有AB∥EC?请证明你的结论。
23.(本题6分)已知关于x的一元二次方程 ax2+x—a=0 ( a≠0 )
(1) 求证:对于任意非零实数a,该方程恒有两个异号的实数根;
(2) 设x1、 x2是该方程的两个根,若∣x1∣+ ∣x2∣=4,求a的值。
五、(24小题10分,25小题11分,共21分)
24.西北某地区为改造沙漠,决定从2002年起进行“治沙种草”,把沙漠地变为草地,并出台了一项激励措施:在“治沙种草”过程中,每一年新增草地面积达到10亩的农户,当年都可得到生活补贴费1500元,且每超出一亩,政府还给予每亩a元的奖励.另外,经治沙种草后的土地从下一年起,平均每亩每年可有b元的种草收入.下表是某农户在头两年通过“治沙种草”每年获得的总收入情况:
| 年 份 | 新增草地的亩数 | 年总收入 |
| 2002年 | 20亩 | 2600元 |
| 2003年 | 26亩 | 5060元 |
(注:年总收入=生活补贴费+政府奖励费+种草收入)
⑴试根据以上提供的资料确定a,b的值;
⑵从2003年起,如果该农户每年新增草地的亩数均能比前一年按相同的增长率增长,那么2005年该农户通过“治沙种草”获得的年总收入将达到多少元?
25.已知:如图,在平面直角坐标系中,点C在![]() 轴上,以C为圆心,4cm为半径的圆与
轴上,以C为圆心,4cm为半径的圆与![]() 轴相交于点A、B,与
轴相交于点A、B,与![]() 轴相交于D、E,且︵AB=︵BD 。点P是⊙C上一动点(P点与A、B点不重合)。连结BP、AP。
轴相交于D、E,且︵AB=︵BD 。点P是⊙C上一动点(P点与A、B点不重合)。连结BP、AP。
(1)求∠BPA的度数;
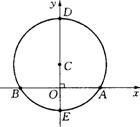 (2)若过点P的⊙C的切线交
(2)若过点P的⊙C的切线交![]() 轴于点G,是否存在点P,使△APB与以A、G、P为顶点的三角形相似?若存在,求出点P的坐标;若不存在,说明理由。
轴于点G,是否存在点P,使△APB与以A、G、P为顶点的三角形相似?若存在,求出点P的坐标;若不存在,说明理由。
梅州市2005年中考数学模拟试题(二)参考答案
1.5,3,1.
2.x≠-2. 3.60° ![]() /2. 4.1.22×1 010. 5.(1,2),(1,-2).
/2. 4.1.22×1 010. 5.(1,2),(1,-2).
6、2,-1,6. 7.8,4 5°. 8.4. 9.1 50. 10. 155π 1 1.C. 1 2.D. 13.D. 1 4.A. 15.C.
16.![]() 17。原式=x/(x-1) 将x=
17。原式=x/(x-1) 将x=![]() +1代入原式(3+
+1代入原式(3+![]() )/3 18。x1= —1, x2=
)/3 18。x1= —1, x2=![]()
19.(1)设这个二次函数的解析式为:y=ax2+bx+c,图象经过点(0,0),(1,-3),(2,-8),∴ 解得a=-1,b=-2,c=O,
∴这个二次函数的解析式为:y=-x2-2x;
(2)它的对称轴为x=-1,顶点坐标为(-1,1).
20.AB=AC,.AB2=AD·AE .AB=2![]()
21.(1)过点A作AD⊥BC于D.由题意,得∠C=4 5°,∠B=30°(或∠BAC=105°),在Rt△ADC中,∴∠C=4 5°,AC==30![]() ,CD=AD=3O,在Rt△ABD中,∵∠B=30°,AD=30,∴AB=60,
,CD=AD=3O,在Rt△ABD中,∵∠B=30°,AD=30,∴AB=60,
 BD=AB
cos30°=30
BD=AB
cos30°=30![]() .甲船从C处追赶上乙船所用的时间:60÷1
5-2=2(小时); (2)在△ABC中,∵BC=CD+BD=30+30
.甲船从C处追赶上乙船所用的时间:60÷1
5-2=2(小时); (2)在△ABC中,∵BC=CD+BD=30+30![]() ,∴(3 0+30
,∴(3 0+30![]() )÷(4-2)=15(1+
)÷(4-2)=15(1+![]() )(千米/时) 答:(1)甲船从C处追上乙船用了2小时. (2)甲船追赶乙船的速度是每小时1
5(1+
)(千米/时) 答:(1)甲船从C处追上乙船用了2小时. (2)甲船追赶乙船的速度是每小时1
5(1+![]() )千米.
)千米.
22.(1)证明:①∵BC为⊙O2的切线 ∴∠D=∠FCE
又∠F=∠F∴⊿FDC∽⊿FCE。
②在⊙O1中,∠B=∠D,
又∠FCE=∠B。∴AB∥EC
(2)仍有AB∥EC。∵ABCD是⊙O1的内接四边形,∴∠FBA=∠FDC
∵BC为⊙O2的切线,∴∠FCE=∠FDC∴∠FCE=∠FBA,∠∴AB∥EC。
23。(1)证明:∵⊿=1+4a2, ∴⊿>0 ∴方程恒有两个实数根
设方程的两根为x1,x2, ∵a≠0, ∴x1·x2= —1<0∴方程恒有两个异号的实数根 (2)∵x1·x2<0, ∴∣x1∣+∣x2∣=∣x1 — x2∣=4
∴∣x1 — x2∣=(x1+x2)2 — 4x1 x2=16
又∵x1+x2= —![]() , ∴
, ∴![]() +4=16。∴a=±
+4=16。∴a=±![]()
24。(1)1500+(20-10)a=2600,
1500+(26-10)a+20b=5 060.
解之得:a=110 b=90
答:a的值是110,b的值是90.
(2)2003年的增长率为30%.
2004年新增草地亩数为 26×(1+30%)=33.8(亩).
2005年新增草地亩数为 26×(1+30%)x=43.94(亩).
2005的总收入为1500+(43.94-10)×110+(20+26+33.8)×90=12 415.4(元).
答:2005年该农户通过“治沙种草"获得的年总收入达到12 415.4元.
25.(1)∠BPA=60°或∠BPA=120°;
(2)设存在点P,使△APB与以点A、G、P为顶点的三角形相似.
i.当P在弧EAD上时,(图1).GP切0 C于点P,∴∠GPA=∠PBA 又∵∠GAP是△ABP的外角,∴∠GAP>∠BPA,∠GA P>∠PBA.欲使△APB与以点A、G、P为顶点的三角形相似,须∠GAP=∠PAB=9O°..BP为⊙C的直径.在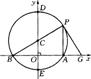 Rt△PAB中,∠BPA=60°,PB=8,..·PA=4,AB=4
Rt△PAB中,∠BPA=60°,PB=8,..·PA=4,AB=4![]() OA=2
OA=2![]() ∴P(2
∴P(2![]() ,4).
,4).
ii.当P在弧EBD上时,(图2)在△PAB和△GAP中,∵∠PBA是△GBP的外角,
∴∠PBA>∠PGB.又∵∠PAB=∠GAP,欲使△APB与以点A、G、P为顶点的三角形相似,须∠APB=∠PGB∴GP切⊙C于点P,∴∠GPB=∠PAG 由三角形内角和定理知:∠ABP=∠GBP ∴∠ABP=∠GBP=90°
在Rt△PAB,∠BPA=60°,PA=8,∴PB=4,AB=4![]() ∴OB=2
∴OB=2![]() ∴P(-2
∴P(-2![]() ,4).∴存在点P1(2
,4).∴存在点P1(2![]() ,4)、P2(-2
,4)、P2(-2![]() ,4)使△APB与以点A、G、P为顶点的三角形相似.
,4)使△APB与以点A、G、P为顶点的三角形相似.