试卷类型:A

东营市二○○五年中等学校招生考试（大纲卷）

数 学 试 题

注意事项：

1． 本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷4页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共12页，满分120分，考试时间为120分钟．

2． 答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上，考试结束，试题和答题卡一并收回．

3． 第Ⅰ卷每题选出答案后，必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．

4． 考试时，允许使用科学计算器．

第Ⅰ卷（选择题　共36分）

一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分．

1.下列运算正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(A)　　　　　　　　　　　　  (B) 　　

(C)　　　 　　 　　　  (D)

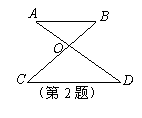2. 如图，AB∥CD，AD，BC相交于O点，∠BAD=35°,

∠BOD=76°，则∠C 的度数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

(A)31°　　　　　　　　　　　　　　　　 (B)35°

(C)41°　 　　　　　　　　　　　　　　　 (D)76°

3. 在反比例函数(k<0)的图象上有两点A(x₁，y₁)，B(x₂，y₂)，且>>0，则的值为　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　

　　(A)正数　　　　　　　　　　　　　　　　　(B)负数　　

(C)非正数　　  　　　　　　　　　　　 (D)非负数

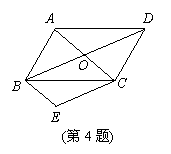4. 如图，平行四边形ABCD中，对角线AC，BD

相交于点O，将△AOD平移至△BEC的位置，

则图中与OA相等的其它线段有　

(A)1条　　　　　　　　　　　　　　　 (B)2条　　

(C)3条　　　　　　　　　　　　　　　 (D)4条

5. 两个不相等的实数m，n满足，，则mn的值为

　　　 (A)　6　　　　　　　　　　　　　　 　　　(B)　 －6　　

(C)　4　　　 　　　　　　　　　　　　　　(D)　－4

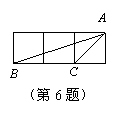6. 如图，小正方形的边长均为1，则下列图中的

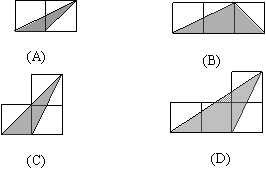三角形（阴影部分）与△ABC相似的是　

7．学校计划将120名学生平均分成若干个读书小组，若每个小组比原计划多1人，则要比原计划少分出6个小组，那么原计划要分成的小组数是

(A)40　　　　　　　　　　　　　　　　　　　　　　　　(B)30　　　

(C)24　　　　　　　　　　　　　　　　　　　　 　　　 (D)20

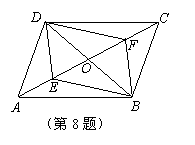8. 如图，在□ABCD中，对角线AC，BD

相交于点O，E，F是对角线AC上的两

点，当E，F满足下列哪个条件时，四

边形DEBF不一定是平行四边形

（A）AE=CF　　　　　　　　　　　　　 （B）DE= BF

（C）∠ADE=∠CBF　　　　　　　　（D）∠AED=∠CFB

9．不等式组的解集是，则m的取值范围是

(A) m≤2　　　　　　　　　　　　　　　　 　　　  (B) m≥2　

(C) m≤1　 　　　　　　　　　　　　　　　　　 (D) m>1

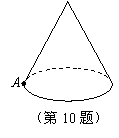10. 如图，圆锥的母线长是3，底面半径是1，

A是底面圆周上一点，从点A出发绕侧面

一周，再回到点A的最短的路线长是

(A)　　　　　　　　　　　　　　　　　　 (B)

(C)　　　　　　　　　　　 　　　　　　 (D)3

11. 在直角坐标系中，O为坐标原点，已知A（1，1），在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数共有　　　　　  　　　　

（A）4个　　　　　　　　　　　　　　　　　　　　　　　　（B）3个

（C）2个　　　　　　　　　　　　　　　　　　　　　　　　（D）1个　　

12. 水池有2个进水口，1个出水口，每个进水口进水量与时间的关系如图甲所示，出水口出水量与时间的关系如图乙所示．某天0点到6点，该水池的蓄水量与时间的关系如图丙所示.

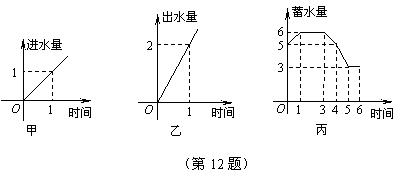下面的论断中：①0点到1点，打开两个进水口，关闭出水口；②1点到3点，同时关闭两个进水口和一个出水口；③3点到4点，关闭两个进水口，打开出水口； ④5点到6点，同时打开两个进水口和一个出水口．

可能正确的是　 　　　　　　　　　　　　　　　

(A)①③　 　　　　　　　　　　　　　　　　　　　 (B)①④　　

(C)②③　　　　　　　　　　　　　　　　　　　　 (D)②④

　　　　　　　　　　　　　　　　　　　　　　　 

试卷类型:A

东营市二○○五年中等学校招生考试（大纲卷）

数 学 试 题

第Ⅱ卷（非选择题　共84分）

注意事项：

　1．第Ⅱ卷共8页，用钢笔或圆珠笔直接写在试卷上．

2．答卷前将密封线内的项目填写清楚．

题号	二	三							总分
		18	19	20	21	22	23	24
得分

二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分．

13. 台湾是我国最大的岛屿，总面积为35 989.76平方千米，这个数据用科学记数法表示为___________平方千米（保留两位有效数字）.

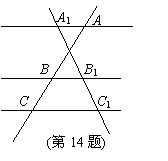
14. 如图，直线 A₁A∥BB₁∥CC₁，若AB=8，BC=4，A₁B₁＝6，则线段B₁C₁的长是_____________.

15. 已知正六边形ABCDEF内接于⊙O，图中阴影部分的面积为，则⊙O的半径为______________________．

16. 已知抛物线经过点A(－2,7)，B(6,7)，C(3,－8)，则该抛物线上纵坐标为－8的另一点的坐标是__________．

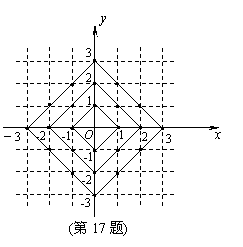
17．在平面直角坐标系中，横坐标、纵

坐标都为整数的点称为整点. 观察图

中每一个正方形（实线）四条边上的

整点的个数，请你猜测由里向外第10

个正方形（实线）四条边上的整点个

数共有_________个.

三、解答题：本大题共7小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤．

18． (本题满分6分)

已知，求的值．

19． (本题满分9分)

时代中学七年级准备从部分同学中挑出身高差不多的40名同学参加校广播体操比赛，这部分同学的身高（单位：厘米）数据整理之后得到下表．

身高x（厘米）	频数	频率
152≤x<155	6	0.1
155≤x<158	m	0.2
158≤x<161	18	n
161≤x<164	11
164≤x<167	8
167≤x<170	3
170≤x<173	2
合计

（1）表中m＝_______，n＝_________．

（2）身高的中位数落在哪个范围内？请说明理由．

（3）应选择身高在哪个范围内的学生参加比赛？为什么？

20． (本题满分9分)

如图，⊙O₁和⊙O₂外切于点P，直线AB是两圆的外公切线，A，B为切点，试判断以线段AB为直径的圆与直线O₁O₂的位置关系，并说明理由．

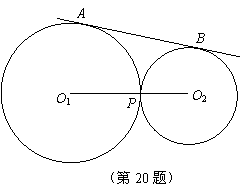
21． (本题满分10分)

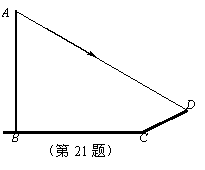
如图:学校旗杆附近有一斜坡．小明准备测量学校旗杆AB的高度，他发现当斜坡正对着太阳时，旗杆AB的影子恰好落在水平地面和斜坡的坡面上，此时小明测得水平地面上的影长BC=20米，斜坡坡面上的影长CD=8米，太阳光线AD与水平地面成26°角，斜坡CD与水平地面BC成30°的角，求旗杆AB的高度（精确到1米）．

22． (本题满分10分)

某水果批发市场香蕉的价格如下表：

购买香蕉数 (千克)	不超过 20千克	20千克以上 但不超过40千克	40千克以上
每千克价格	6元	5元	4元

张强两次共购买香蕉50千克（第二次多于第一次），共付出264元， 请问张强第一次、第二次分别购买香蕉多少千克？

23． (本题满分10分)

如图甲，四边形ABCD是等腰梯形，AB∥DC. 由4个这样的等腰梯形可以拼出图乙所示的平行四边形．

（1）求四边形ABCD四个内角的度数；

（2）试探究四边形ABCD四条边之间存在的等量关系，并说明理由；

（3）现有图甲中的等腰梯形若干个，利用它们你能拼出一个菱形吗？若能，请你画出大致的示意图．

24． (本题满分10分)

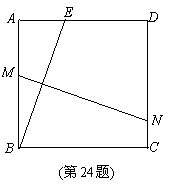
如图，在正方形ABCD中，AB＝2，E是AD边上一点（点E与点A，D不重合）． BE的垂直平分线交AB于M，交DC于N.

（1）设AE＝x，四边形ADNM的面积为S．写出S关于x的函数关系式；

（2）当AE为何值时，四边形ADNM的面积最大？最大值是多少？