2005年全国各地中考分类解析——解直角三角形
一、选择题:
 1.(泰山)一人乘雪橇沿坡比1∶
1.(泰山)一人乘雪橇沿坡比1∶![]() 的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)
的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)
间的关系为s =10t+2t2,若滑到坡底的时间为4秒,则此人下降的高度为
A.72
m B.36![]() m C.36
m D.18
m C.36
m D.18![]() m
m
2、(大连)张华同学的身高为1.6米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树的影长为6米,则这棵树的高为( )
 A. 3.2米 B.4.8米 C.5.2米 D.5.6米
A. 3.2米 B.4.8米 C.5.2米 D.5.6米
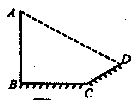
3.(湖北黄石)小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30º角,且此时测得1米杆的影长为2米,则电线杆的高度为( )
A.9米 B.28米 C.![]() 米 D.
米 D.![]() 米
米
|
 4河南)如图,
4河南)如图,
|
|
|
|
 5.(兰州)如果sin2α+sin2300=1那么锐角α的度数是( )
5.(兰州)如果sin2α+sin2300=1那么锐角α的度数是( )
A.150 B.300 C.450 D.600
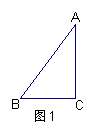
6. (厦门) 如图1,在直角△ABC中,∠C=90°,若AB=5,AC=4,
则sin∠B=
A. B. C. D.
7.(黑龙江)在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在地面上的影长为40米,则古塔高为 ( )
(A)60米 (B)40米 (C)30米 (D)25米
二、填空题:
 1、(嘉兴)图7是引拉线固定电线杆的示意图。已知:CD⊥AB,CD
1、(嘉兴)图7是引拉线固定电线杆的示意图。已知:CD⊥AB,CD![]() m,∠CAD=∠DBD=60°,则拉线AC的长是___________m.
m,∠CAD=∠DBD=60°,则拉线AC的长是___________m.

2、(四川内江)如图河对岸有一古塔AB,小敏在C处测得塔顶A的仰角为α,向塔前进Sm到达D,在D处测得A的仰角为β,则塔高为 米。
3.(沈阳)在△![]() 中,
中,![]() ,
,![]() ,
,![]() 30º,则
∠BAC
的度数是 .
30º,则
∠BAC
的度数是 .
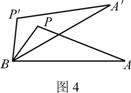 4. (四川资阳)如图4,如果△APB绕点B按逆时针方向旋转30°后得到
4. (四川资阳)如图4,如果△APB绕点B按逆时针方向旋转30°后得到
△A'P'B,且BP=2,那么PP'的长为____________.
(不取近似值. 以下数据供解题使用:sin15°=![]() ,cos15°=
,cos15°=![]() )
)
5.(惠安)同一时刻,一竿的高为1.5米,影长为1米,某塔影长为20米,则塔的高为 米.
14.(兰州)锐角A满足2sin(A-150)=![]() 则∠A=____
则∠A=____
6、(梅州市)求值:sin230°+cos230°= 。
三、解答下列各题
1.(泰山)高为12.6米的教学楼ED前有一棵大树AB(如图1).
(1)某一时刻测得大树AB、教学楼ED在阳光下的投影长分别是BC=2.4米,DF=7.2米,求大树AB的高度.(3分)
(2)用皮尺、高为h米的测角仪,请你设计另一种测量大树AB高度的方案,要求:
①在图2上,画出你设计的测量方案示意图,并将应测数据标记在图上(长度用字母m 、n …表示,角度用希腊字母α、β …表示);(3分)
②根据你所画的示意图和标注的数据,计算大树AB高度(用字母表示).(3分)
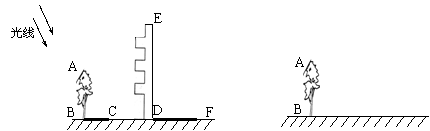
图1 图2
解:连结AC、EF
(1)∵太阳光线是平行线∴AC∥EF∴∠ACB=∠EFD
∵∠ABC=∠EDF=90°∴△ABC∽△EDF……………………………1分
∴![]() ∴
∴![]() ∴AB=4.2……………………2分
∴AB=4.2……………………2分
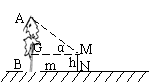 答:大树AB的高是4.2米.………………………………………3分
答:大树AB的高是4.2米.………………………………………3分
(2)(方法一)
…………………………6分
如图MG=BN=m
AG=m tanα ∴AB=(m tanα+h)米 ………………………9分
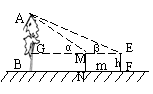 |
(方法二)
…………………………6分
∴ AG =![]() ∴AB=
∴AB=![]() +h …………………9分
+h …………………9分
或AB=![]() +h
+h
(不加测角仪的高扣2分,其他测量方法,只要正确均可得分)
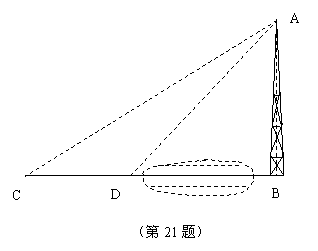 2.(嘉兴)如图,河对岸有一铁塔AB。在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为45°,求铁塔AB的高。
2.(嘉兴)如图,河对岸有一铁塔AB。在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为45°,求铁塔AB的高。
解:在Rt△ABD中,∵∠ADB=45°,∴BD=AB。 ……2分
在Rt△ABC中,∵∠ACB=30°,∴BC=![]() AB。 ……2分
AB。 ……2分
设AB=x(米),∵CD=16,∴BC=x+16.∴x+16=![]() x ……2分
x ……2分
![]() 。即铁塔AB的高为
。即铁塔AB的高为![]() 米。
米。
另解:在Rt△ABC中,∵∠ACB=30°,∴BC=ABcot30° ……2分
在 Rt△ABD中,∵∠ADB=45°,∴BD=ABcot45° ……2分
∵CD=BC-BD=16,∴ ABcot30°- ABcot45°=16 ……2分
∴![]()
即铁塔AB的高为
![]() 米 ……2分
米 ……2分
3. (锦州)如图,一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在北偏东65°45′的方向上,渔船向正东方向航行l小时45分钟之后到达D点,观测到灯塔B恰好在正北方向上,已知两个灯塔之间的距离是12海里,渔船的速度是16海里/时,又知在灯塔C周围18.6海里内有暗礁,问这条渔船按原来的方向继续航行,有没有触礁的危险?
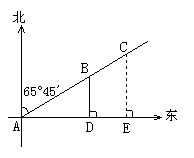
评价要求:此题解法不惟一,只要合理,即可赋分.
解:1小时45分=![]() 小时.
小时.
在Rt△ABD中,![]() (海里),
(海里),
∠BAD=90°-65°45′=24°15′. ……2分
∵cos24°15′=![]() ,
,
∴![]() (海里). ……4分
(海里). ……4分
AC=AB+BC=30.71+12=42.71(海里).
在Rt△ACE中,sin24°15′=![]() ,
,
∴CE=AC·sin24°15′=42.71×0.4107=17.54(海里).
∵17.54<18.6,∴这条船不改变方向会有触礁危险. ……8分
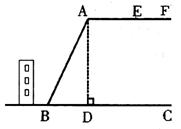
4.(宁德)6月以来,我省普降大雨,时有山体滑坡灾害发生。北峰小学教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示:AF∥BC,斜坡AB长30米,坡角ÐABC=65º。为了防止滑坡,保障安全,学校决定对该土坡进行改造,经过地质人员勘测,当坡角不超过45º时,可以确保山体不滑坡。
(1)求坡顶与地面的距离AD等于多少米?(精确到0.1米)
(2)为确保安全,学校计划改造时保持坡脚B不动,坡顶A沿AF削进到E点处,求AE至少是多少米?(精确到0.1米)
解:
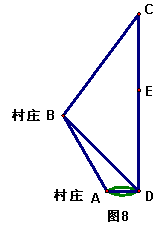
5.(沈阳)如图8所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
 方案一:
方案一:![]() ;
方案二:
;
方案二:![]() .
.
经测量得![]() 千米,
千米,![]() 千米,
千米,![]() 千米,∠BDC=45°,∠ABD=15°.
千米,∠BDC=45°,∠ABD=15°.
已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
⑴求出河宽AD(结果保留根号);
⑵求出公路CD的长;
⑶哪种方案铺设电缆的费用低?请说明你的理由.
6.(玉林)阅读下列材料,并解决后面的问题.
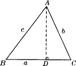 在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.过A作AD⊥BC于D(如图),则sinB=
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.过A作AD⊥BC于D(如图),则sinB=![]() ,sinC=
,sinC=![]() ,即AD=csinB,AD=bsinC,
,即AD=csinB,AD=bsinC,
于是csinB=bsinC,即![]() .
.
同理有![]() ,
,![]() .
.
所以![]() ………(*)
………(*)
即:在一个三角形中,各边和它所对角的正弦的比相等.
(1)在锐角三角形中,若已知三个元素a、b、∠A,运用上述结论(*)和有关定理就可以
求出其余三个未知元素c、∠B、∠C,请你按照下列步骤填空,完成求解过程:
第一步:由条件a、b、∠A ![]()
![]() ∠B;
∠B;
第二步:由条件 ∠A、∠B.![]()
![]() ∠C;
∠C;
第三步:由条件.
![]()
![]() c.
c.
(2)一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以28.4海里/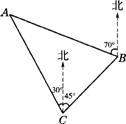 时的速度按北偏东45°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西70°的方向上(如图11),求此时货轮距灯塔A的距离AB(结果精确到0.1.参考数据:sin40°=0.6 4 3,sin65°=0.90 6,sin70°=0.940,sin7 5°=0.9 6 6).
时的速度按北偏东45°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西70°的方向上(如图11),求此时货轮距灯塔A的距离AB(结果精确到0.1.参考数据:sin40°=0.6 4 3,sin65°=0.90 6,sin70°=0.940,sin7 5°=0.9 6 6).
解:(1) ![]() , ∠A+∠B+∠C=180°,a、∠A、∠C或b、∠B、∠C,
, ∠A+∠B+∠C=180°,a、∠A、∠C或b、∠B、∠C,
![]() 或
或![]()
(2)依题意,可求得∠ABC=65°,
∠A=40°. (5分)
BC=14.2.(6分)
AB≈21.3.
答:货轮距灯塔A的距离约为21.3海里.(9分)
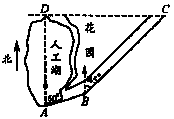 7.(湖北黄石)初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图A、D是人工湖边的两座雕塑,AB、BC是湖滨花园的小路,小东同学进行如下测量,B点在A点北偏东60º方向,C点在B点北偏东45º方向,C点在D点正东方向,且测得AB=20米,BC=40米,求AD的长。
7.(湖北黄石)初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图A、D是人工湖边的两座雕塑,AB、BC是湖滨花园的小路,小东同学进行如下测量,B点在A点北偏东60º方向,C点在B点北偏东45º方向,C点在D点正东方向,且测得AB=20米,BC=40米,求AD的长。
(![]() ,结果精确到0.01米)
,结果精确到0.01米)
8. (江苏宿迁)某数学兴趣小组,利用树影测量树高.已测出树AB的影长AC为9米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,试求树影的最大长度.
(计算结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

解:(1)在Rt△A BC中,∠BAC=90°,∠C=30°
 ∵tanC=
∵tanC=![]() ………2分
………2分
∴AB=AC·tanC ………3分
=9×![]() ………4分
………4分
≈5.2(米) ………5分
(2)以点A为圆心,以AB为半径作圆弧,当太阳光线与圆弧相切时树影最长,点D为切点,DE⊥AD交AC于E点,(如图) ………7分
在Rt△ADE中,∠ADE=90°,∠E=30°,
∴AE=2AD ………9分
=2×5.2=10.4(米) ………10分
答:树高AB约为5.2米,树影有最长值,最长值约为10.4米.……11分
9、(南通)如图,为了测量一条河的宽度,一测量员在河岸边的C处测得对岸一棵树A在正南方向,测量员向正东方向走180米到点B处,测得这棵树在南偏西60°的方向,求河的宽度(结果保留根号).
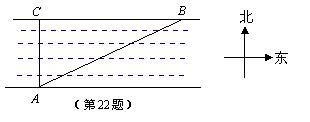 略解:河宽为
略解:河宽为![]() 米.
米.
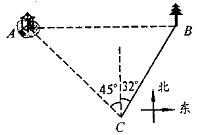 10、(河南课改)如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?(结果精确到1米。参考数据:sin32°=0.5299,cos32°=0.8480)
10、(河南课改)如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?(结果精确到1米。参考数据:sin32°=0.5299,cos32°=0.8480)
解:过点C做CD⊥AB,垂足为D,
∵B点在A点的正东方向上,∴∠ACD=45°,∠DCB=32°,
在Rt△BCD中,BC=100,
∴![]() (米)
(米)
![]() (米),
(米),
在Rt△ACD中,AD=CD,
 ∴
∴![]() (米)。
(米)。
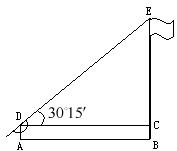
11.(惠安)如图,在离旗杆40米的A处,用测角仪器测得旗杆顶的仰角为![]() ,已知测角仪器高AD=
,已知测角仪器高AD=![]() 米,求旗杆的高度BE(精确到 0.1米,供选用的数据:
米,求旗杆的高度BE(精确到 0.1米,供选用的数据: ![]()
![]()
![]()
![]()
![]()
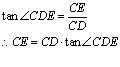 解:
解:
![]()
![]()
![]() 答:旗杆的高度约24.9米.---------(8分)
答:旗杆的高度约24.9米.---------(8分)
12. (兰州)如图9某海关缉私艇巡逻到达A处时接到情报,在A处北偏西600方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向前进,上级命令要对可疑船只进行检查,该艇立即沿北偏西450的方向快速前进,经过1小时的航行,恰好在C处截住可疑船只,求该艇的速度(结果保留整数
,![]() ≈2.449,
≈2.449,![]() ≈1.732
≈1.732![]() ≈1.414)
≈1.414)
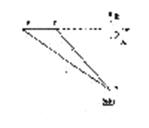
解:如图所示,在RtADC中,∠DAC=450∴设AD=DC=x(海里), 则AC=x 海里,在RtADB中,∠ADB=900∠DAB=600
∴∠B=300 ∴BD=AD即24+x=x∴x=12+1
∴AC=·12+1=12+ ≈46(海里) ∴V==46(海里/时)
答:该艇的速度约为46海里/时
13.(四川泸洲)随着社会的发展,人们对防洪的意识越来越强,今年为了提前做好防洪准备工作,某市正在长江边某处常出现险情的河段修建一防洪大坝,其横断面为梯形ABCD,如图7所示,根据图中数据计算坝底CD的宽度(结果保留根号).
解:在Rt△ADF中,∠D=60°,![]() ……………………1分
……………………1分
∴DF=AF·cotD
=9×cot60°
=9×![]() ……………………………………………………3分
……………………………………………………3分
又在Rt△BEC中
∵∠C=45°, ∴△BEC为等腰三角形
∴EC=BE=9……………………………………………………………6分
在矩形AFEB中,FE=AB=10………………………………………7分
∴DC=DF+FE+EC
=![]()
 =
=![]()
答:坝底DC的宽为![]() ………………………………………8分
………………………………………8分
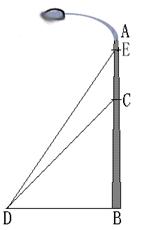
14.(浙江台州) 如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,则 BC的长度是多少?现再在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果保留三个有效数字)
解:在R t△BCD中,∵ BD=5, ∴ BC=5![]() =
4.1955≈4.20.
……4分
=
4.1955≈4.20.
……4分
在R t△BCD中,BE=BC+CE= 6.20, ………………5分
∴ DE=![]() …………………6分
…………………6分
=![]() =
=![]()
≈7.96 ………………………9分
答:BC的长度约为4.20![]() ,钢缆ED的长度约7.96
,钢缆ED的长度约7.96![]() .………10分
.………10分
(若BC=4.1955暂不扣分,但是ED的长度未保留三个有效数字扣1分)
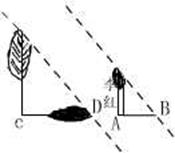 15.(湖北十堰)(1)在一个宁静的夜晚,月光明媚,张芳和身高为1.65m的李红两位同学在人民广场上玩。张芳测得李红的影长为1m,并立即测得小树影长为1.5m,请你估算小树的高约为多少?
15.(湖北十堰)(1)在一个宁静的夜晚,月光明媚,张芳和身高为1.65m的李红两位同学在人民广场上玩。张芳测得李红的影长为1m,并立即测得小树影长为1.5m,请你估算小树的高约为多少?
(1)![]() ……………………2分
……………………2分
答:小树高约为2.4m……………………3分
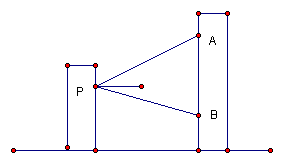
16、(梅列区)某中学政教处在九年级进入学业考试总复习前,将一幅激励同学拼搏的标语悬挂在教学楼前。有位学生在与这幢教学楼相距20米的办公楼P处测得标语顶端A点的仰角为15°,底部B的俯角为10°,请你根据这位同学测定的数据,计算出这幅标语的长度。(精确到0.01米)