2005年中考数学复习同步检测(28) 姓名
(圆的基本性质2)
一.填空题:
1.一条弦把圆分成![]() 两部分,则劣弧所对的圆心角的度数是 ;
两部分,则劣弧所对的圆心角的度数是 ;
2.等边△ABC内接于⊙O,∠AOB= 度;
3.四边形ABCD是⊙O的内接四边形,且∠A∶∠B∶∠C =2∶3∶6,则∠D = 度;
 4.⊙O的半径为4 cm,若线段OA的长为10 cm,则OA的中点B在⊙O的___________,若线段OA的长为6 cm,则OA的中点B在⊙O的___________;
4.⊙O的半径为4 cm,若线段OA的长为10 cm,则OA的中点B在⊙O的___________,若线段OA的长为6 cm,则OA的中点B在⊙O的___________;
5.如图,在A地往南40 m的B处有一幢民宅,东30 m的C处
有一变电设施,在BC的中点D处有一古建筑,因施工需要必须
在A处进行一次爆破,为使民宅、变电设施、古建筑都不遭到破
坏,则爆破影响面的半径r应控制的范围为_____________________;
 6.如图,在⊙O中,AB = BC = CD,∠BAD =
6.如图,在⊙O中,AB = BC = CD,∠BAD =![]() ,则∠AED = 度;
,则∠AED = 度;
 7.如图,在⊙O中,AB是直径,∠CAB =
7.如图,在⊙O中,AB是直径,∠CAB =![]() ,则∠CBA = 度,
,则∠CBA = 度,
∠BOC = 度,图中⊿BOC为 三角形;
8.在⊿ABC中,D是AB的中点,且CD =![]() AB,
AB,
若AC =![]() ,BC =
,BC =![]() ,则AB =
,则AB = ![]() ;
;
9.矩形的四个顶点在同一圆上,这个圆的圆心是该矩形___________ ,
这个圆的半径是该矩形______________;
10.一个点到圆的最大距离为1l cm,最小距离为5 cm,则圆的半径为_____________;
二.选择题:
11.在直角坐标系中,以O(0,0)为圆心,以5为半径画圆,则点A(![]() ,
,![]() )的位置在 ( )
)的位置在 ( )
A ⊙O内 B ⊙O上 C ⊙O外 D 不能确定
12.下列语句中正确的个数是 ( )
 ①平行四边形的四个顶点在同一圆上;②矩形的四个顶点在同一圆上;③菱形的四个顶点在同一圆上;④正方形四边中点在同一圆上;
①平行四边形的四个顶点在同一圆上;②矩形的四个顶点在同一圆上;③菱形的四个顶点在同一圆上;④正方形四边中点在同一圆上;
A 1个 B 2个 C 3个 D 4个
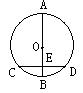
13.已知:如右图,AB是⊙O的直径,CD是弦,AB⊥CD于点E,
若AB=10,CD = 6,则BE的长是 ( )
 A 4 B 3 C 2 D 1
A 4 B 3 C 2 D 1
14.在⊙O中,C是弧AB的中点,连结AB、AC、BC,则 ( )
A AB>2AC B AB=2AC
C AB<2AC D 不能确定
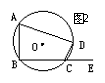
15.如图2,四边形ABCD内接于⊙O,点E在BC延长线上.若∠A=50o,则∠DCE等于 ( )
A 40o B 50o C 70o D 130o
16.下面说法正确的是 ( )
A.弦相等,则弦心距相等 B.弧长相等的弧所对的弦相等
C.垂直于弦的直线必平分弦 D.圆的两条平行弦所夹的弧长相等
17.下列语句中,正确的个数是 ( )
 ①相等的圆心角所对的弧相等;②同圆或等圆中,相等的圆周角所对的弦相等;
①相等的圆心角所对的弧相等;②同圆或等圆中,相等的圆周角所对的弦相等;
③一边上的中线等于这条边一半的三角形是直角三角形;
④等弧所对的圆周角相等;
⑤一条弧所对的圆心角等于它所对的圆周角的一半
A 2个 B 3个 C 4个 D 5个
18.已知弓形的弦长为![]() ,弓形高为1,则弓形所在圆的半径为
( )
,弓形高为1,则弓形所在圆的半径为
( )
 A 2 B
A 2 B ![]() C
C ![]() D 13
D 13
19.如图,圆弧形桥拱的跨度AB=12米,拱高CD = 4米,
则拱桥的半径为 ( )
A 6.5米 B 9米 C 13米 D 15米
20.在△ABC中,∠A=70°,⊙O截△ABC的三边,所截得的弦都
相等则∠BOC等于 ( )
A. 115° B. 125° C. 130° D. 不能确定
21.已知AB是⊙O的直径,C为⊙O上一点,作CD⊥AB,垂足为D延长CD到E,使
DE=CD,则点E和⊙O的位置关系是 ( )
A.点E在⊙O上 B.点E在⊙O外 C.点E在⊙O内 D.以上都有可能
22.有4个命题:①直径相等的两个圆是等圆;②长度相等的两条弧是等弧;③圆中最大的弦是通过圆心的弦;④一条弦把圆分为两条弧,这两条弧有可能是等弧.其中真命题是( )
 A. ①③ B. ①③④ C. ①④ D. ①
A. ①③ B. ①③④ C. ①④ D. ①
23.如图7—6所示,P是直径AB上的一点,且PA=2 cm,
PB = 6 cm,CD是过P点的弦,那么下列PC与PD的长度中,
不符合题意的是 ( )
 A.1 cm,12 cm B.3 cm,5 cm c.7 cm,
A.1 cm,12 cm B.3 cm,5 cm c.7 cm,![]() cm D.3 cm,4 cm
cm D.3 cm,4 cm
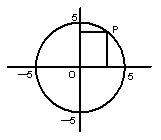
24.如图7—7,P(x,y)是以坐标原点为圆心,
5为半径的圆周上的点,若![]() ,
,![]() 都是整数,
都是整数,
则这样的点共有 ( )
A. 4个 B. 8个 C. 12个 D. 16个
三.解答题:
25.如图,有一座石拱桥的桥拱是以O为圆心,OA为半径的一段圆弧。若∠AOB=120°,OA = 4米,请求出石拱桥的高度。

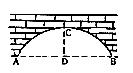
26.某存在村口建一个如图所示形状的门楼,半圆拱的圆心距离地面![]() ,半径为
,半径为![]() ,现有一辆高
,现有一辆高![]() ,宽
,宽![]() 的集装箱卡车,问是否能通过这个门楼,请写出结论再说出理由。(以下数据供计算参考:
的集装箱卡车,问是否能通过这个门楼,请写出结论再说出理由。(以下数据供计算参考:![]() ,
,![]() ,
,![]() )
)
 |
27.已知,如图,AD是⊿ABC的外角∠EAC的角平分线,交BC的延长线于D,延长DA交⊿ABC的外接圆于点F,连结FB、FC;
 (1)求证:FB = FC;(2)求证:FB
(1)求证:FB = FC;(2)求证:FB![]() = FA
= FA![]() FD;(3)若AB是⊿ABC的外接圆的直径,∠EAC = 120
FD;(3)若AB是⊿ABC的外接圆的直径,∠EAC = 120![]() ,BC = 6 cm,求AD的长;
,BC = 6 cm,求AD的长;
28.已知,如图,AD是⊿ABC的外角∠EAC的平分线,AD与三角形ABC的外接圆相交于点D,求证:DB = DC;

29.已知,如图,⊿ABC中,AB = AC,AF为⊿ABC的高,在⊿ABC的外接圆AC上任取一点P,连结AP,交BC的延长线于E,求证:⊿ABP∽⊿AEB;
