2005年中考数学复习同步检测（10）　　　　　　  姓名　　　　 

（一次函数）

一．填空题：

1．点（，），（,）在函数的图像上，则；

2．正比例函数的图像经过点（，）,则函数的关系式是　　　　　　　  ；

3．函数与轴的交点是　　　　　  ，与轴的交点是　　　　　　 ，与两坐标轴围成的三角形面积是　　　　  ；

4．函数与轴的交点是　　　　　  ，与轴的交点是　　　　　  ；

5．直线不经过第四象限，则的取值范围是_________，的取值范围_________；

6．当直线与直线平行时，；

7．一次函数的图像是___________，因此作一次函数图像时,只要确定________个点，再经过这________个点作_________就可以了；

8．正比例函数的关系式是________　　　　___，从图像上看，正比例函数与一般一次函数相比，特殊性在于：______________________________；

9．已知点A坐标为(，)，B点坐标为(，)，C点坐标为(，)，其中在直线上的点有__________　　　__，在直线上的点有_______　　　____；

10．函数的图象不经过第　 　　　 象限；

11．正比例函数的图像一定经过点 　　　　；

12．若点（，）在一次函数的图像上，则　　　；

13．一次函数的图像经过点（，0）,则；

14．某地的电话月租费24元，通话费每分钟0.15元，则每月话费（元）与通话时间（分钟）之间的关系式是　　　　　　　　　　 ，某居民某月的电话费是38.7元，则通话时间是　　　　 分钟，若通话时间62分钟，则电话费为　　　　　  元；

二．选择题：　　　　　　　　　　　　　　　　　　　　　　　　　　　 

15．下列函数中，正比例函数是 　　　　　　　　　　　　　　　　　　　　　　 （　　）

A　　 　　 B　　 　　　C　　　　 D　　

16．若一次函数，则其图象经过　　　　　　　　　　　  （　　）

A 第一、二、三象限　B　第一、三、四象限　C 第一、二、四象限 D　第二、三、四象限

17．李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速前进，结果准时到校，在课堂上，李老师请学生画出：自行车行进路程Ｓ（千米）与行进时间t（小时）的函数图象的示意图，同学们画出的示意图如下，你认为正确的是　　　　　　　　　　　　　　  （　　）

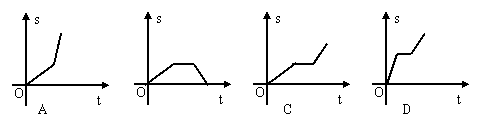　　　　　　　　　　  B

18．已知一次函数与的图像都经过A(,)，且与轴分别交于B、C两点,则△ABC的面积为 　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A.　　　  4　　　  B.　　　　5　　　　 C.　　　　 6　　　　 D.　　　7

19．在直线且到轴或轴距离为1的点有　　　　　　　　　　　  （　　）

A.　　　 1个　　　 B.　　　 2个　　　 C.　　　 3个　　　　 D.　　 4个

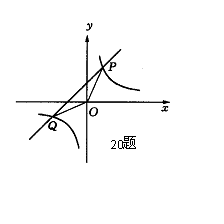
20．已知直线与轴的交点在轴的正半轴，下列结论：①，②，③ ，④ 其中正确的有 　　　　　　　　（　　）

A.　　　 1个　　　 B.　　　 2个　　　 C.　　　 3个　　　　 D.　　 4个

21．点A(,)和B(,)都在直线上，则与的关系是　　　　 （　　）

A.　　 ≤　　 B.　　 =　　  C.　　　<　　　 D.　　>

22．点P(,)关于轴的对称点在第三象限，那么直线的图像不经过（　　）

 A.　　第一象限　　B.　　 第二象限　　 C.　　　第三象限　　 D.　 第四象限

23．若一次函数的图像经过(,)和点(, ),则这个函数的图像不经过（　　）

A.　　第一象限　　B.　　 第二象限　　 C.　　　第三象限　　 D.　 第四象限

24．与直线平行的直线是　　　　　　　　　　　　　　　　　　　　  （　　）

A　　　　　B　　　　　　C　　 　 D　　

三．解答题：

25．作出函数的图像,并回答下列问题:

(1) 的值随值的增大怎样变化?

(2) 图像与轴的交点坐标是什么?与轴的交点坐标呢?

(3) 若函数与的图像交于轴上同一点,你能求出的值吗?

(4) 若一个正比例函数的图像与的图像互相平行,请写出此正比例函数解析式,并说明理由.

26．为了保护学生的视力，课桌椅的高度是按一定的关系配套设计的。研究表明：假设课桌的高度为cm，椅子的高度（不含靠背）为cm，则应是的一次函数，右边的表中给出两套符合条件的桌椅的高度：

	第一套	第二套
椅子高度（cm）	40.0	37.0
桌子高度（cm）	75.0	70.2

（1）请确定与的函数关系式；

（2）现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配套？请通过计算说明理由。

27．某单位计划10月份组织员工到外地旅游，估计人数在6～15人之间。甲、乙量旅行社的服务质量相同，且对外报价都是200元，该单位联系时，甲旅行社表示可给予每位游客八折优惠；乙旅行社表示，可先免去一位游客的旅游费用，其余游客九折优惠。

①　　 分别写出两旅行社所报旅游费用与人数的函数关系式；

②若有11人参加旅游，应选择那个旅行社？

③人数在什么范围内，应选甲旅行社；在什么范围内，应选乙旅行社？　

28．如图，l_A l_B分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。

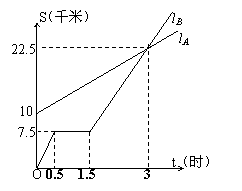（1）B出发时与A相距　　　千米；

（2）走了一段路后，自行车发生故障，进行　　　　　

修理，所用的时间是　　 小时；

（3）B出发后　　小时与A相遇；

（4）若B的自行车不发生故障，保持出发时

的速度前进，　　 小时与A相遇，相遇点

离B的出发点　　  千米。在图中表示出

这个相遇点C；

（5）求出A行走的路程S与时间t的函数关系式。（写出过程）