2005年中考数学复习同步检测（12） 姓名
（反比例函数）
一．填空题：
1.
与
成反比，且当＝6时，
，这个函数解析式为 ；
2.函数
和函数
的图像有 个交点；
3.反比例函数
的图像经过（－
，5）点、（
，－3）及（10，
）点，则
＝ ，＝ ，＝
；
4.若函数
是正比例函数，那么
，图象经过 象限；
5.若反比列函数
的图像经过二、四象限，则= _______
6.已知
-2与
成反比例，当=3时，=1，则与间的函数关系式为
；
7．已知正比例函数
与反比例函数
的图象都过A（
，1），则＝ ，正比例函数与反比例函数的解析式分别是
、
；
8．设有反比例函数
，
、
为其图象上的两点，若
时，
，则的取值范围是___________
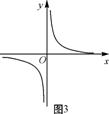
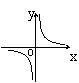
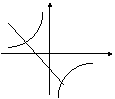
9．右图3是反比例函数
的图象，则k与0的大小关系是k 0.
10．函数
的图像，在每一个象限内，随的增大而 ；
11．反比例函数
在第一象限内的图象如图，点M是图像上一点， MP垂直轴于点P，如果△MOP的面积为1，那么的值是
；
12．
是关于的反比例函数，且图象在
13．对于函数
，当
时,随的
而减小；
14．当
时，函数
是反比例函数；
15．函数的图像，在每一个象限内，随的增大而 ；
16．在平面直角坐标系内，从反比例函数
的图象上的一点分别作、轴的垂
线段，与、轴所围成的矩形面积是12，那么该函数解析式是
；
17．.已知
与
成正比例，且当
时，
，那么与之间的函数关系
是 ；
二．选择题：
18．下列函数中，反比例函数是 （ ）
A 
B 
C 
D 
19．已知反比例函数的图像经过点（，），则它的图像一定也经过
（ ）
A (－,－) B (,－) C (－，) D （0，0）
20．如果反比例函数的图像经过点（－3，－4），那么函数的图像应在
（ ）
A 第一、三象限 B 第一、二象限 C 第二、四象限 D 第三、四象限
21．若与－3成反比例，与
成正比例，则是
的
（ ）
A 正比例函数 B 反比例函数 C 一次函数 D 不能确定
22．若反比例函数
的图像在第二、四象限，则的值是
（ ）
A －1或1 B 小于
的任意实数 C －1
Ｄ 不能确定
23．函数的图象经过点（－4，6），则下列各点中不在图象上的是 （ ）
A （3，8） B （3，－8） C （－8，－3） D （－4，－6）
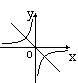
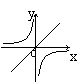
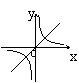
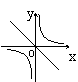24．正比例函数和反比例函数在同一坐标系内的图象为
（ ）
A B C D
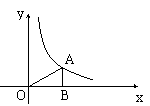
25．如上右图，A为反比例函数图象上一点，AB垂直轴于B点，若S△AOB＝3，则的值为
（ ）
A 6 B 3 C D 不能确定
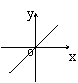
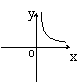
26．矩形的面积为6cm2，那么它的长cm与宽cm之间的函数关系用图象表示大致（ ）
A B C D
27．在同一直角坐标平面内，如果直线
与双曲线
没有交点，那么
和
的关系一定是
（ ）
A <0，>0 B >0，<0 C 、同号
D 、异号
28．已知变量与成反比例，当
时，
；那么当=3时，的值是 （ ）
A 6 B ―6 C 9 D ―9
29．当路程
一定时，速度
与时间之间的函数关系是
（ ）
A 正比例函数 B 反比例函数 C 一次函数 D 二次函数
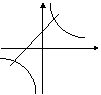
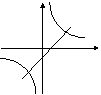
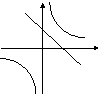
30．在同一坐标系中，函数
和
的图像大致是 （ ）
A B C D
31．已知反比例函数
的图像上有两点A(
，
)，B(
，
)，且
，则
的值是
（ ）
A 正数 B 负数 C 非正数 D 不能确定
三．解答题：
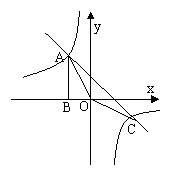
32．如图，Rt△ABO的顶点A是双曲线与直线
在第二象限的交点，AB⊥轴于B且S△ABO=
（1）求这两个函数的解析式
（2）求直线与双曲线的两个交点A，C的坐标和△AOC的面积。
33．如图，一次函数
的图像与反比例函数
的图像相交于A、B两点，
（1）利用图中条件，求反比例函数和一次函数的解析式
（2）根据图像写出使一次函数的值大于反比例函数的值的的取值范围；
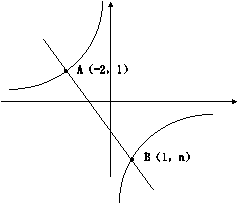
34．如图，已知一次函数
的图象与轴、轴分别交于A、B两点，且与反比例函数
的图象在第一象限内交于C点,CD垂直于轴，垂足为点D，若OA=OB=OD=1.
（1） 求点A、B、D的坐标；
（2） 求一次函数和反比例函数的解析式。
y
 |
C
B
A o
D
x