2005年中考数学复习同步检测（13）　　　　　　  姓名　　　　 

（二次函数概念）

一．填空题：

1．二次函数的图象开口方向　　　  ，顶点坐标是　　　　 ，对称轴是　　　　　  ；

2．函数的图象在轴上截得的两个交点距离为 　　　　；

3．函数，当为　　　  时，函数的最大值是　　　　　 ；

4．二次函数与轴的两交点在轴正半轴上，则的取值范围是　　　　　　 ；

5．把函数的图象向右平移3个单位，再向下平移2个单位，得到的二次函数解析式是　　　　　　　  ；

6．若二次函数的最大值为，则常数；

7．直线与抛物线只有一个交点，则；

8．若、、为△ABC的三边，且二次函数的顶点在轴上，则△ABC为　　　　　 三角形；

9．抛物线与轴交于A、B两点，与轴交于正半轴C点，且AC = 20，BC = 15，∠ACB = 90°，则此抛物线的解析式为　　　　　　　　　　　 ；

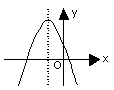
10．若二次函数的图象如图所示，则直线

不经过　　　　  象限；

11．抛物线在直线下方的的取值范围是　　　　　　  ；

12．已知抛物线的对称轴为，且经过点（1，4）和点（5，0），则该抛物线的解析式为　　　　 　　　　　；

13．抛物线的顶点坐标是__________，对称轴是　　　　　 ；

14．已知抛物线的图象与轴有两个交点，那么一元二次方程的根的情况是　 　　　　　　　　　　　；

15．已知抛物线与轴交点的横坐标为－1，则＝　　　　  ；

16．一次函数的图象过点（，1）和点（，），其中> 1，则二次函数的顶点在第 　　  象限；

二．选择题：　　　　　　　　　　　　　　　　　　　　　　　　　　　 

17．已知二次函数、、、它们图象的共同特点为（　 ）

A　都关于原点对称，开口方向向下 　　　　 B　都关于轴对称，随的增大而增大

C　都关于轴对称，随的增大而减小　　D　都关于轴对称，顶点都是原点

18．若二次函数的图象经过原点，则的值必为　　  （　　）

A　　或3　　 B　　　　　　C、　　　3　　 　D、　　无法确定

19．将二次函数的图象向左平移2个单位后，再向下平移2个单位，得到（　　）A　= ² + 5　 B　　C　　D　

 20．二次函数的图象开口向上，顶点在第四象限内，且与轴的交点在轴下方，则点（）在　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A　　 第一象限 　 B　　 第二象限 　　C　　　第三象限 　　D　　第四象限

21．二次函数，则它的图象必经过点　　　　　　　 （　　）

A　 （，）  B　　（，） 　 C　　 （，） 　D　　（，）

22．已知二次函数若，则其图象与轴的位置关系是　　  （　　）

A　只有一个交点　 B　　有两个交点　　C　　 没有交点　　D　 交点数不确定

23．函数为的二次函数，其函数的开口向下，则的取值为（　　）

A  B　 　 C  　 D 

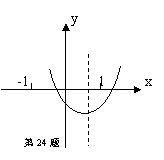
24．已知函数的图象如图所示，则下列判断不正确的是　　　（　　）

A　 　B　　C　　D

25．已知点A（1,）、B（）、C（）

在函数上，则、、的大小关系是

A　＞＞ B　＞＞C　＞＞ D  ＞＞

26．已知（2，5）（4，5）是抛物线上的两点，则这个抛物线的对称轴为（　　）A　　　　 B　　　　　C　　　　　D　　

三．解答题：

27．抛物线过(,)、(1，4)、(2，7)三点，求抛物线的解析式；

28．二次函数有最小值为，且：：=1：2：()，求此函数的解析式；

29．抛物线的对称轴是，且过（4，－4）、（－1，2），求此抛物线的解析式；

30．二次函数，时；时；时，；求此函数的解析式；

31．已知二次函数．

（1）　　　 求证：不论为何实数值，这个函数的图象与轴总有交点．

（2）　　　 为何实数值时，这两个交点间的距离最小？这个最小距离是多少？

 

 

 

 

 32．已知二次函数的图象与轴分别交于A（-3，0），B两点，与轴交于（0，3）点，对称轴是，顶点是P．求：（1）函数的解析式；（2）△APB的面积．

33．有一个抛物线形拱桥，其最大高度为16m，跨度为40m，现把它的示意图放在平面直角坐标系中如 图（4），求抛物线的解析式