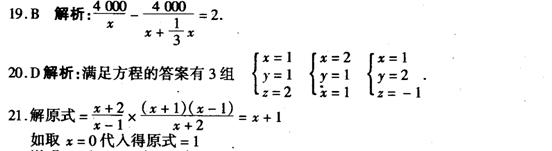贵州省毕节地区2005年初中毕业升学统一数学考试
(满分120分 考试时间120分钟)
一、填空题：(每小题2分，共20分)
1．
的倒数是_________。
2．分解因式：ax―a=_________________。
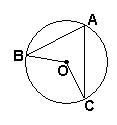
3．如图，A、B、C是⊙O上三点，∠BOC=150º，则∠A=_______。
4．如果a+2+
=0，那么a、b的大小关系为a_____b
(填“＞”“=”或“<”)
5．要做一个底面直径为acm，高为bcm的圆柱侧面模型，
要剪裁的长方形纸片的面积为__________。
6．等腰梯形的上底长为2，下底长为4，高为1，那么下底角的正弦值是_______。
7．某同学解分式方程
=0，得出原方程的解为x=1或x=—1。你认为他的解答对吗?请你作出判断，并说明理由______________________________。
8．三角形三边的长分别为3，4，x，那么三角形的周长y与边长
x的函数关系式是_______，x的取值范围是_____________。
9．反比例函数y=
(m为常数)的图像如图所示，则m的
| 点的个数 | 线段的条数 |
| 2 | 1 |
| 3 | 3 |
| 4 | 6 |
| 5 | 10 |
| 6 | 15 |
| 7 |
取值范围是________。
10．一条直线上有若干个点，
以任意两点为端点可以确
定一条线段，线段的条数
与点的个数之间的对应关
系如下表所示。请你探究
表内数据间的关系，根据
发现的规律，填写表中空格。
二、选择题：(以下每小题均有四个答案，其中有且只有一个是正确的，每小题3分，共30分)
11．关于―(―a)2的相反数，有下列说法：①等于a2；②等于(―a)2；③值可能为0；④值一定是正数。其中正确的有( )
A．1个 B．2个 C．3个 D．4个
12．直线y=kx+1一定经过点( )
A．(1，0) B．(1，k) C．(0，k) D．(0，1)
13．以下列各组数为边长，能构成直角三角形的是( )
A．
，
，
B．，
， C．32，42，52 D．1，2，3
14．已知⊙O和三点P、Q、R，⊙O的半径为3，OP=2，OQ=3，OR=4，经过这三点中的一点任意作直线总是与⊙O相交，这个点是( )
A．P B．Q C．R D．P或Q
15．AB、DC是圆的两条平行弦，则ABCD一定不是( )
A．等腰梯形 B．直角梯形 C．正方形 D．矩形
16．适合
=3―a的正整数a的值有( )
A．1个 B．2个 C．3个 D．4个
17．当你将一把扇形扇子逐渐打开时，容易发现打开部分的扇形面积随圆心角的变化而变化，那么下列函数中能正确描述这种变化的是( )
A．正比例函数 B．反比例函数 C．一次函数(b≠0) D．二次函数
18．方程组
的解是
，那么方程x2+ax+b=0( )
A．有两个不相等实数根 B．有两个相等实数根 C．没有实数根 D．有两个根为2和3
19．某乡镇改造农村电网，需重新架设4000米长的电线。为了减少施工对农户用电造成的影响，施工时每天的工作效率比原计划提高
，结果提前2天完成任务，问实际施工中每天架设多长电线?如果设原计划每天架设x米电线，那么列出的方程是( )
A．
―
=2 B．―=2 C．
―=2 D．―=2
20．小明、小敏、小新商量要在毕业前夕给老师办公室的4道窗户剪贴窗花表达大伙的尊师之情，今年是农历鸡年，他们设计了金鸡报晓的剪纸图案。小明说：“我来出一道数学题：把剪4只金鸡的任务分配给3个人，每人至少1只，有多少种分配方法?”小敏想了想说：“设各人的任务为x、y、z，可以列出方程x+y+z=4。”小新接着说：“那么问题就成了问这个方程有几个正整数解。”现在请你说说看：这个方程正整数解的个数是( )
A．6个 B．5个 C．4个 D．3个
三、解答题：(本大题共7个小题，共70分)
21．(本题满分6分)
先将分式(1+
)÷
进行化简，然后请你给x选择一个合适的值，求原式的值。
22．(本题满分8分)
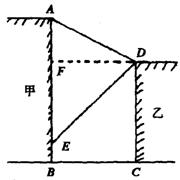如图，在甲建筑物上从A到E悬挂一条条幅，在乙建筑物顶部D点测得条幅顶端A点的仰角为30º，测得条幅底端E点的俯角为45º，若甲、乙两建筑物之间的水平距离为30米，求条幅AE的长。(结果精确到个位，参考数据=1.732)
23．(本题满分10分)
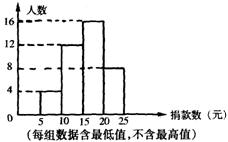我区某中学对学生会倡导的“献爱心”捐款活动进行
抽样调查，被调查的学生捐款情况如图所示。
(1)该校共调查了______名学生。
(2)捐款15元以上的学生频率是_______。
(3)若该校共有1800名学生，估计全校学生一共
捐款至少多少元?
24．(本题满分10分)
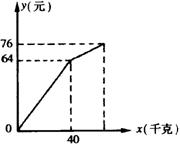小明在暑期社会实践活动中，以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售，在销售了40千克西瓜之后，余下的每千克降价0.4元，全部售完。销售金额与售出西瓜的千克数之间的关系如图所示。
请你根据图像提供的信息完成以下问题：
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的
函数关系式。
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
25．(本题满分10分)
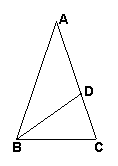如图，已知△ABC中，D是AC边上一点，∠A=36º，∠C=72º，∠ADB=108º。
求证：(1)AD=BD=BC；
(2)点D是线段AC的黄金分割点。
26．(本题满分12分)
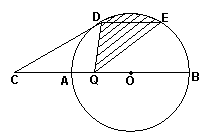如图，AB是⊙O的直径，点C是BA延长线上一点，CD切⊙O于D点，弦DE∥CB，Q是AB上一动点，CA=1，CD是⊙O半径的倍。
(1)求⊙O的半径R。
(2)当Q从A向B运动的过程中，图中阴影部分的
面积是否发生变化，若发生变化，请你说明理由；若
不发生变化，请你求出阴影部分的面积。
27．(本题满分14分)
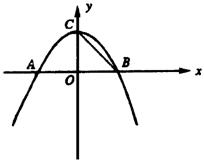如图，抛物线y=―x2+(6―
)x+m―3与x轴交于A(x1，0)、B(x2，0)两点(x1＜x2)，交y轴于C点，且x1+x2=0。
(1)求抛物线的解析式，并写出顶点坐标及对称轴方程。
(2)在抛物线上是否存在一点P使△PBC≌△OBC，
若存在，求出点P的坐标，若不存在，请说明理由。
贵州省毕节地区2005年初中毕业升学统一数学考试答案
